2020-04-07
124
Второй метод Ляпунова дает необходимые и достаточные условия устойчивости линейных динамических систем. Рассмотрим систему следующего вида:
где 
- матричное уравнение Ляпунова. Линейная система устойчива, если для положительно определенной квадратичной формы ее полная производная в силу уравнений системы будет отрицательно определенной квадратичной формой.
Для оценки знака квадратичной формы применяется критерий Сильвестра:
матрица В является положительной, а соответствующая квадратичная форма положительно определенная, если все ее диагональные миноры будут положительны. 
; В - отрицательная матрица, если все нечетные миноры будут отрицательны, а четные положительны, 
.
Последовательность проверки устойчивости линейных систем
1) Выбирается вид исследуемой функция, например,
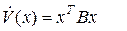
2) Формируется матрица квадратичной формы в виде:
3) Записывается матричное уравнение Ляпунова:
.
4) Выполняется решение матричного уравнения, либо по известным А и В определяется С, либо определяется В по заданным А и С
5) Оценивается знак квадратичной формы и делается вывод об устойчивости системы.
Пример
Исходные данные:
.
Решение:
1) 
, пусть 
,
2) 
,
3) 
из полученной системы находим значения элементов квадратичной формы В и оцениваем ее знак.
