Градиентный алгоритм относится к базовым алгоритмам адаптации. Вектор градиента всегда направлен в сторону максимального локального роста функции. Следовательно, если вектор скорости настраиваемых параметров ( ) направить в сторону антиградиента
) направить в сторону антиградиента 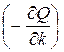 , то реализуется последовательный спуск в локальный минимум
, то реализуется последовательный спуск в локальный минимум
 (4.1)
(4.1)
Проведем синтез адаптивной системы для одноканального линейного объекта управления
 (4.2)
(4.2)
где u, y – управляющая и выходная переменные соответственно. Параметры объекта ai, bj точно не определены, но заданы (n + m + 1) – мерной областью возможных значений Wab. Операторная запись уравнения (4.2) имеет вид
 (4.3)
(4.3)
где an (p) = pn + an-1 pn-1 + …+ a0, bm (p) = bm pm + bm-1 pm-1 + … + b0, pi = di / d ti – оператор i - кратного дифференцирования.
Цель управления зададим предельным соотношением
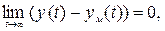 (4.4)
(4.4)
где yм (t) – эталонная траектория движения, которая удовлетворяет уравнению эталонной модели
 (4.5)
(4.5)
здесь  r – эталонное входное воздействие на систему. Оператор
r – эталонное входное воздействие на систему. Оператор  является устойчивым, т.е. корни уравнения
является устойчивым, т.е. корни уравнения  имеют отрицательную действительную часть.
имеют отрицательную действительную часть.
Для определения структуры «идеального» закона управления выполним преобразования уравнений (4.2) и (4.5). Вычтем из обеих частей уравнения (4.3) выражение (an (p) y):
0 = bm (p) u – an (p) y. (4.6)
Полагая y = yм, запишем уравнение (4.5)
 . (4.7)
. (4.7)
Прибавим к обеим частям уравнения (6) выражение ( ):
):
 (4.8)
(4.8)
где  Далее вычтем из (4.8) уравнение (4.5):
Далее вычтем из (4.8) уравнение (4.5):
 (4.9)
(4.9)
где e = y – yм. Пусть “идеальный” закон управления имеет вид
 (4.10)
(4.10)
тогда
 (4.11)
(4.11)
Так как полином  является устойчивым по условию, то e ® 0 при t ® ¥, т.е. закон управления (4.10) позволяет обеспечить выполнение цели управления (4.4). Учитывая неизвестность bm (p) и D n-1 (p), реальный закон управления запишем в виде
является устойчивым по условию, то e ® 0 при t ® ¥, т.е. закон управления (4.10) позволяет обеспечить выполнение цели управления (4.4). Учитывая неизвестность bm (p) и D n-1 (p), реальный закон управления запишем в виде
 (4.12)
(4.12)
с операторами 
Если в процессе настройки коэффициентов будет выполнено 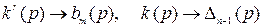 при t® ¥, то e ® 0, что показывает достижение поставленной цели управления.
при t® ¥, то e ® 0, что показывает достижение поставленной цели управления.
Для определения целевой функции введем новое рассогласование (s), которое возникает в результате замены yм на y в уравнении эталонной модели (4.5),
 (4.13)
(4.13)
Если вычесть из (4.13) уравнение (4.5), то получим уравнение, описывающее связь между рассогласованиями e и s:
 (4.14)
(4.14)
Из (4.14) следует, что если s ® 0 при t® ¥, то в силу устойчивости  имеем e ® 0 при t ® ¥. Следовательно, будет выполнена поставленная цель. Это позволяет задать целевую функцию в виде
имеем e ® 0 при t ® ¥. Следовательно, будет выполнена поставленная цель. Это позволяет задать целевую функцию в виде
 (4.15)
(4.15)
Выполним преобразования уравнения (4.13). Просуммируем уравнения объекта (4.8) и регулятора (4.12):
 ,
,
приведем подобные и учтем (4.13):
 (4.16)
(4.16)
Введем обозначения для вектора неизвестных параметров

вектора настраиваемых параметров

и вектора координатных переменных
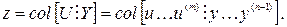
Уравнение для рассогласования (16) примет вид
 . (4.17)
. (4.17)
Алгоритм настройки коэффициентов согласно (4.1), (4.15), (4.17) имеет вид

или  .
.
 2020-04-07
2020-04-07 198
198








