Проблема оптимального по времени управления начала интенсивно изучаться математиками в 50-е годы 20 столетия. В 1953-1957 гг. Р Беллман, Л.С. Понтрягин, В.Г. Болтянский, Р.В. Гамкрелидзе, Н.Н. Красовский, Ж. Ла-Саль развили основы теории задачи о минимальном времени перехода. Принцип максимума был впервые провозглашен на международном конгрессе математиков, который проходил в Эдинбурге в 1958 г.
Теоремы принципа максимума справедливы для динамических систем, модель которых можно записать в пространстве состояний:

где 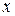 - вектор координат состояния,
- вектор координат состояния,  - вектор управляющих воздействий, причем
- вектор управляющих воздействий, причем  , U – множество допустимых значений u. Задача состоит в определении закона изменения управляющего воздействия, которое переведет систему из начального состояния
, U – множество допустимых значений u. Задача состоит в определении закона изменения управляющего воздействия, которое переведет систему из начального состояния  в некоторое конечное
в некоторое конечное 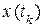 за время Т, обеспечив экстремальное значение функционалу
за время Т, обеспечив экстремальное значение функционалу
 .
.
Введем дополнительную переменную
 ,
,
т.е. расширим вектор состояния. Дифференциальное уравнение для новой переменной имеет вид:
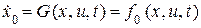 .
.
Тогда расширенная система дифференциальных уравнений запишется в виде:
 .
.
В принципе максимума особую роль играют вспомогательные переменные  , и функция
, и функция
 .
.
Последнее выражение определяет элементы вектора  , для которых справедливо следующее выражение
, для которых справедливо следующее выражение

или 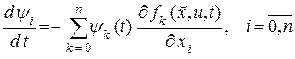 .
.
Нетрудно видеть, что
 ,
,
так как  . Запишем полученную систему соотношений
. Запишем полученную систему соотношений

 ,
,
данные уравнения являются канонически сопряженными.
Основная теорема принципа максимума:
Для оптимальности управления u(t) и траектории  необходимо существование такой ненулевой непрерывной функции
необходимо существование такой ненулевой непрерывной функции  , соответствующей функциям u(t) и
, соответствующей функциям u(t) и  в силу уравнений исходной системы, что при любом
в силу уравнений исходной системы, что при любом  , функция
, функция  переменного
переменного  достигает в точке
достигает в точке  максимума:
максимума:
 .
.
Последовательность решения задачи с помощью принципа максимума:
1. Модель объекта управления записывается в пространстве состояний и вводится новая переменная состояния:
 .
.
2. Составляется функция Н:
 .
.
3. Определяется значение u(t), максимизирующее функцию Н:

4. Определяются элементы вектор-функции  :
:
 .
.
5. Записывается искомое оптимальное управление через  .
.
Особенностью принципа максимума является то, что вариационная задача нахождения функции u(t), обеспечивающая экстремум функционалу  , заменена более простой задачей математического анализа – задачей определения u(t) из условия максимума вспомогательной функции
, заменена более простой задачей математического анализа – задачей определения u(t) из условия максимума вспомогательной функции 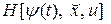 .
.
Пример 1. Решается задача:  , где
, где  – траектория развития процесса,
– траектория развития процесса,  – управление.
– управление.
Найти: 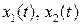 и
и  , удовлетворяющие условию:
, удовлетворяющие условию:
W=  .
.
Решение. Решим данную задачу с использованием принципа максимума. Введем функцию 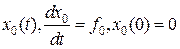 , где
, где  .
.
Тогда исходную систему можно представить в виде

Введем функцию  ,где
,где 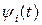 – неизвестные функции времени, тогда
– неизвестные функции времени, тогда 
Запишем сопряженную систему:  Решении данной системы в развернутом виде может быть представлена следующим образом:
Решении данной системы в развернутом виде может быть представлена следующим образом:

Запишем 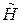 в явном виде
в явном виде

и найдем экстремум этой функции по u:

Таким образом закон изменения оптимального управления имеет вид 
Для нахождения оптимальной траектории движения объекта нужно подставить u(t) в исходную систему, тогда

 2020-04-07
2020-04-07 143
143








