Часть 2. Второй метод Ляпунова. Основные понятия

         Динамическая система описывается дифференциальными уравнениями вида:

Пусть - расстояние от точки до начала координат. Для устойчивой системы 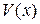 уменьшается при увеличении времени, а для неустойчивой  увеличивается при увеличении времени. Полагаем, что функция  удовлетворяет условиям:

т.е. - положительная знакоопределенная функция. Функция называется знакоопределенной (положительно или отрицательно), если она сохраняет свой знак для любых значений переменных состояния и обращается в ноль в начале координат. Если функция задана в виде квадратичной формы [2, с.98], то ее знак можно определить критерием Сильвестра [2, с.99] либо по собственным значениям квадратной матрицы коэффициентов. Полная производная рассматриваемой функции в силу уравнений системы (производной функции вдоль траектории движения системы) и согласно принятым обозначениям, , имеет вид:

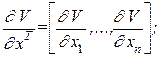
Теоремы второго метода Ляпунова

Теорема об асимптотической устойчивости: система будет асимптотически устойчива, если для положительно определенной функции Ляпунова ее полная производная в силу системы будет отрицательно определенной функцией,

В теореме сформулированы достаточные условия устойчивости нелинейных динамических систем.

Теорема об экспоненциальной устойчивости: система будет экспоненциально устойчива, если для положительно определенной функции Ляпунова ее полная производная в силу системы будет отрицательно определенной функцией, причем обе эти функции будут удовлетворять квадратичным ограничениям:

Теорема о неустойчивости:с истема неустойчива, если для положительно определенной функции  ее полная производная в силу уравнений системы является также положительно определенной функцией.

    Если условия не выполняются условия приведенных теорем, то исследование системы следует выполнить другим методом.