Виды неопределённостей

В зависимости от источника неопределенности различают неопределенность модели динамической системы, неопределенность внешних условий и целевую неопределенность. Математическая модель может быть неопределенна как структурно, так и параметрически. Параметрическая неопределённость означает зависимость свойств (характеристик) ОУ от неизвестных параметров (массы, момента инерции, коэффициента жесткости и т. д.). Параметрическая неопределённость может быть априорной или текущей. Параметры могут быть неизвестными постоянными или медленно меняющимися по сравнению с другими процессами в замкнутой системе. Принято соотносить темп изменения параметров с темпом переходного процесса или темпом изменения переменных состояния объекта. Если параметры изменяются медленно по сравнению с изменением состояния объекта (x(t)), то в изменениях переменных состояния накапливается достаточно информации о дрейфе параметров. Предположение о медленном изменении неизвестных параметров называется гипотезой квазистационарности. Практически это означает, что параметры объекта считаются постоянными или «замороженными». При этом объект называется квазистационарным или «объектом с замороженными коэффициентами».

Параметры могут быть неизвестными и переменными, причем темп их изменения сравним с темпом процессов в объекте управления или темпом изменения внешних воздействий. Динамические системы с таким видом параметрической неопределённости называются нестационарными. Случай параметрической неопределённости объекта является наиболее изученным в теории адаптивного управления.

Пример 1.1. В безредукторном электроприводе вал двигателя непосредственно соединён с нагрузкой. Такая схема применяется, например, в мехатронных поворотных столах. При отсутствии редуктора уравнение вращающихся масс электропривода (без учёта внешнего возмущающего момента) имеет вид:

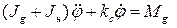(1.1)

где j - угол поворота вала, J_g – момент инерции якоря электродвигателя, J_н – момент инерции нагрузки, k_с – коэффициент скоростного трения, М_g - вращающий момент. Обычно J_н>> J_g, кроме того, во многих практических случаях J_н заранее точно не известен. Как правило, задаются только диапазоном возможных значений J_н, например, J_н_min≤ J_н ≤ J_н_max. Если диапазон значений достаточно широк, то модель (1.1) считается априорно параметрически неопределённой. Введём обозначения в уравнение (1.1): y= j, u= M_g. Если 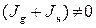для любого момента времени, то, с учётом принятых обозначений, исходное уравнение примет вид: ,
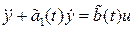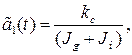
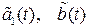где . Коэффициенты характеризуют параметрическую неопределённость.

Значительное влияние на поведение реальных систем управления оказывает окружающая среда (влажность, температура, скорость движения воздушных масс, характеристики нагрузки и т.д.). Неопределённость внешних условий учитывается в математической модели в виде возмущающих воздействий и (или) сигналов задания.

В большинстве практических случаев точная форма (характер поведения) внешних воздействий остаётся неизвестным вплоть до начала работы системы управления. Поэтому внешние условия функционирования реальных систем управления характеризуется высокой степенью неопределённости.

Пример 1.2. В судовых гребных установках используются двухъякорные электроприводы постоянного тока. Момент сопротивления при движении судна с постоянной скоростью имеет две основные составляющие: постоянную, зависящую от скорости судна (М₁), и переменную, которая во многих практических случаях может считаться гармонической, зависящей от частоты качки судна (М₂): M_c = M₁+ M₂, 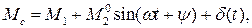где =const, d(t) – нерегулярная составляющая, w - частота качки судна, y - сдвиг по фазе, в общем случае, зависящий от частоты. Как правило, d(t) и w является заранее неизвестными, поэтому М_с считается неопределённым возмущением.

Другим примером служит электропривод постоянного тока, приводящий в движение барабан (катушку), на который наматывается материал (ткань, проволока, металлические листы и т.д.). В процессе работы изменяется масса нагрузки на валу двигателя и, как следствие, моменты инерции и сопротивления.

Неопределённость цели можно иллюстрировать следующими примерами. Наряду с детерминированными задачами пространственного движения, в которых желаемая траектория задана заранее (или может быть определена) существуют плохо определённые (неопределённые) задачи, в которых эталонная траектория задана неточно или её аналитическое описание априорно неизвестно, для формирования управления могут использоваться только текущие измерения отклонений от траектории. Рассматриваемая задача соответствует движению некоторого кинематического механизма вдоль «физически заданного» контура, выявляемого с помощью сенсоров, и характеризуется неопределённостью цели (целевого условия). Такого рода неопределённость часто имеет место при управлении подвижными манипуляционными роботами, если среда функционирования, траектория движения или предметы манипулирования заранее точно не известны, например, робот-«искатель», робот-«уборщик» и т.д. Отсутствие полной информации о траектории движения приводит к тому, что в уравнении регулятора 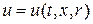эталонное входное воздействие на систему (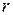) является неизвестным.

Виды возмущений

Неопределённости математической модели и внешних условий учитываются как возмущения в описании динамических систем. Информация о природе и свойствах возмущений используется при определении вида адаптивного регулятора. Разделение возмущений на виды может быть выполнено по разным признакам. Будем различать три основных вида возмущений: параметрические, аддитивные, структурные, и используем аналитическое описание видов возмущений. Рассмотрим модели первых двух видов возмущений. Для этого введём описание номинальной системы: 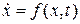, и возмущённой системы: 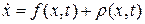, где ρ(х, t) определяет вид возмущения.

1. Если ½ ρ(x, t) ½≤ C₁ ½ х ½ и ρ(0,t) = 0,

где С₁= const, C₁ > 0, то возмущение называется мультипликативным или параметрическим.

Пример 1.3. Пусть номинальная система линейная, f(x,t)=A₀x. Возмущение возникло из-за отклонений параметров матрицы коэффициентов, А=А₀+А₁, от номинальных значений. Возмущённая система имеет вид

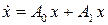
т.е. ρ(x,t)=A₁x. В этом случае С₁= ½ А₁ ½и½ ρ(x,t) ½£ ½ А₁ ½½ х ½.

2. Если для любого x и t выполняются условия ½ ρ(x,t) ½£ С₂ и½ ρ(0,t) ½¹ 0,

то такой вид вариаций математической модели называют аддитивными возмущениями (или постоянно действующими возмущениями). Другое название аддитивных возмущений – сигнальные возмущения.

Пример 1.4. Модель возмущённой системы имеет вид

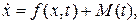½ М(t) ½ £ С₂.

Третий вид возмущений называется сингулярным (или структурным). Для его характеристики представим номинальную модель следующим уравнением

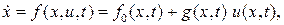(1.2)

где f₀(x, t), g(x, t) – n-мерные вектор – функции, u(x, t) – скалярная функция управляющего воздействия. Структурные возмущения возникают вследствие так называемой, «паразитной динамики». Возмущенная модель может быть определена в виде

(1.3)

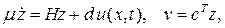z Î R^m (1.4)

где Г, d, c – матрица и векторы постоянных коэффициентов соответствующих размерностей. m - малый постоянный параметр, z – вектор состояния модели. Уравнение (1.4) описывает «паразитную динамику». Пусть справедливо выражение 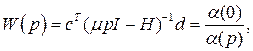где a(р) – гурвицев полином, р=d/dt. Тогда при m близком к 0 имеем

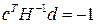Если m достаточно малая величина (), то изменяется структура системы (1.3), (1.4). Поэтому используется термин «структурные возмущения», но из-за того, что меняется порядок системы, такие возмущения называют также сингулярными, а система (1.3), (1.4) – сингулярно возмущенной.