2020-04-07
152
Синусоидального тока
Представление гармонических колебаний комплексными числами
Синусоидальное напряжение (ток) можно представить в виде мнимой части комплексного числа в показательной форме, составленного из амплитуды и фазы функции времени
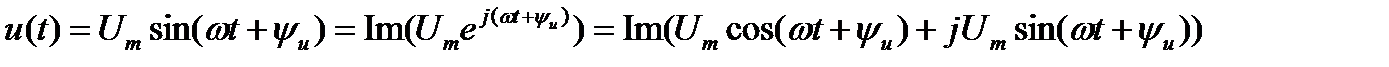
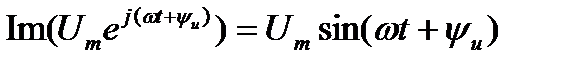
Комплексное число
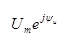
называется комплексной амплитудой напряжения и обозначается
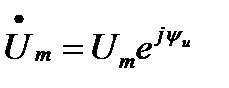
Аналогичным образом можно получить комплексную амплитуду тока
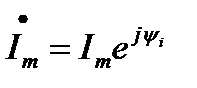
На практике для расчетов электрических цепей синусоидального тока используют комплексы действующего значения напряжения и тока.
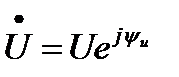
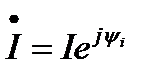
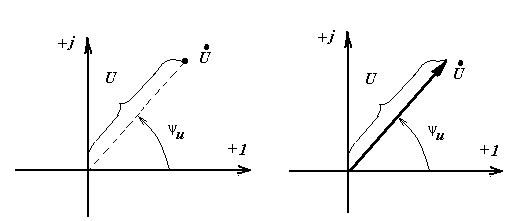
На комплексной плоскости комплексы действующего значения изображают по координатам (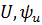
) в полярной системе координат
Напомним, что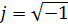 
- это мнимая единица.
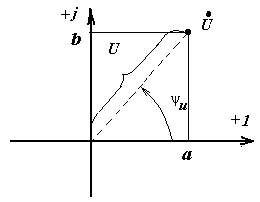
Комплексы в декартовой системе координат
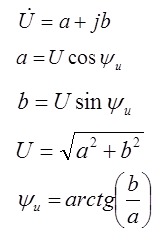
Преобразование синусоидальных токов и напряжений в комплексные числа (комплексные токи и напряжения) позволяет преобразовать тригонометрические уравнения, составленные по законам Кирхгофа для синусоидальных токов и напряжений, в алгебраические уравнения для комплексных токов и напряжений. Решение алгебраических уравнений в комплексных числах оказывается не столь громоздким, как решение тригонометрических уравнений. Решив систему уравнений Кирхгофа относительно комплексных токов, можно затем по комплексным токам определить синусоидальные токи.
Соотношения между комплексными токами и напряжениями на идеализированных элементах электрических цепей
Электрическое сопротивление (резистор)
Если к резистору приложено синусоидальное напряжение, то через него протекает синусоидальный ток. Поставим в соответствие синусоидальному напряжению комплексное напряжение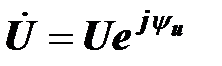 
, а синусоидальному току – комплексный ток 
.
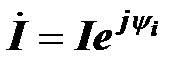Действующее значение напряжения на резисторе пропорционально действующему значению тока
,
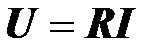Начальная фаза напряжения на резисторе равна начальной фазе тока
.
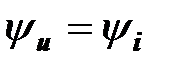Следовательно,
.
Идеальная катушка(индуктивный элемент)
Пусть синусоидальному напряжению на катушке соответствует комплексное напряжение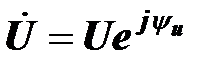 
, а синусоидальному току – комплексный ток .
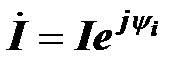Действующее значение напряжения на идеальной катушке пропорционально действующему значению тока
,
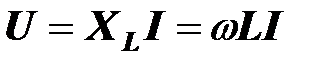где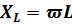 
- индуктивное сопротивление катушки. Напряжение опережает ток по фазе на 90o (
)
.
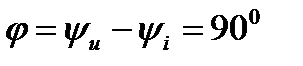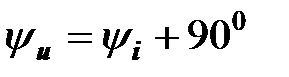Следовательно,
.
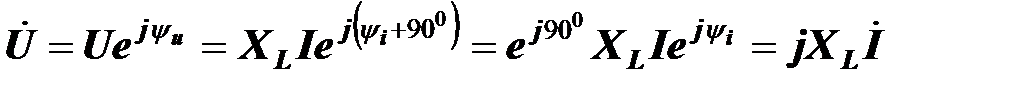Комплексное напряжение на катушке пропорционально комплексному току
,
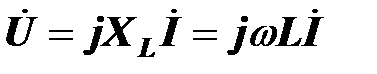коэффициент пропорциональности
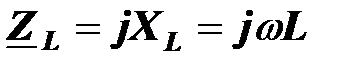
называется комплексным сопротивлением идеальной катушки.
Идеализированный элемент емкость (идеальный конденсатор)
Пусть синусоидальному напряжению на конденсаторе соответствует комплексное напряжение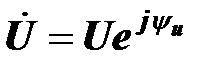 
, а синусоидальному току – комплексный ток .
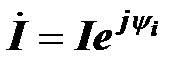Действующее значение напряжения на конденсаторе пропорционально действующему значению тока
,
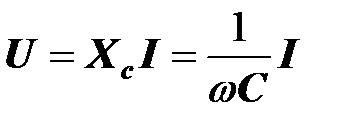где
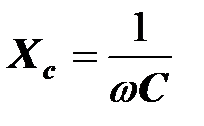
- емкостное сопротивление конденсатора. Напряжение отстает от тока по фазе на 90o (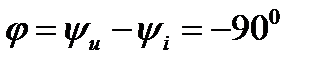
)
.
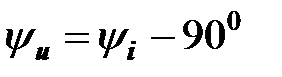Следовательно,
.
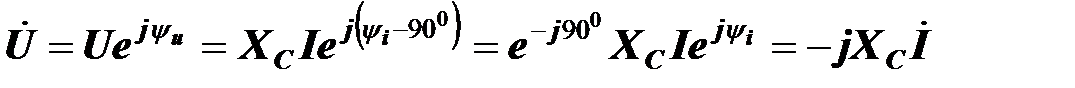Комплексное напряжение на конденсаторе пропорционально комплексному току
,
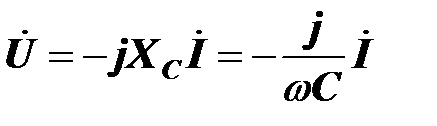коэффициент пропорциональности
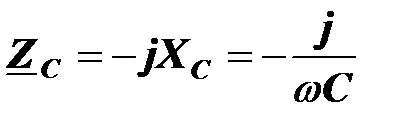
называется комплексным сопротивлением конденсатора
