Так как магнитное поле вихревое, то для упрощения его описания вводят не скалярный, а векторный потенциал А с помощью следующих соотношений
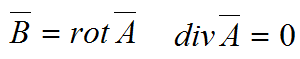
После этого три векторных уравнения, описывающие поле, превращаются в одно векторное

При 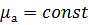 это уравнение принимает вид
это уравнение принимает вид

То есть превращается в векторное уравнение Пуассона
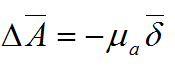
Как известно, магнитный поток определяется как поток вектора магнитной индукции через поверхность S
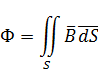
Магнитный поток может быть вычислен и с помощью векторного потенциала. В соответствии с теоремой Стокса

Интеграл по площади заменяется интегралом по контуру, охватывающему эту площадь (теорема Стокса)
Для магнитного поля бесконечно длинного проводника с током векторный потенциал имеет только одну проекцию по направлению провода и определяется по формуле (по аналогии с электростатическим потенциалом бесконечно длинной заряженной нити)
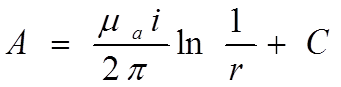
Для двухпроводной линии с током

С учетом представленных выражений для векторного потенциала определим магнитный поток сквозь рамку от двухпроводной линии с током иным способом, чем в предыдущей задаче
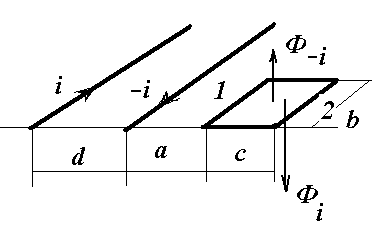
Для стороны рамки 1: r1=a+d, r2=a;
Для стороны рамки 2: r1=a+d+с, r2=a+с;
Определим поток через рамку спомощью циркуляции векторного потенциала по контуру рамки. На сторонах рамки 1 и 2 направление вектоного потенциала совпадает с ориентацией этих сторон, а на двух других сторонах перпендикулярно. При раскрытии интеграла останутся только составляющие сторон рамки 1 и 2. Так как в данной задаче векторный потенциал не изменяется вдоль оси z (по направлению линии), то получим
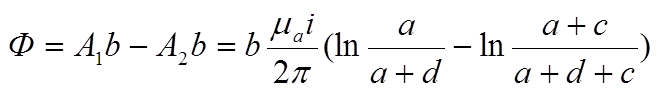
Можно убедится, что результат совпадает с расчетом с помощью вектора магнитной индкуции при интегрировании по площади рамки.
Расчет с помощью потенциала А гораздо эффективнее для случаев, когда плоскость рамки находится под углом к плоскости линии.

На рисунке рамка поворачивается вокруг оси, совпадающей со стороной 1.При повороте плоскости рамки на угол α взаимная индуктивность линии и рамки
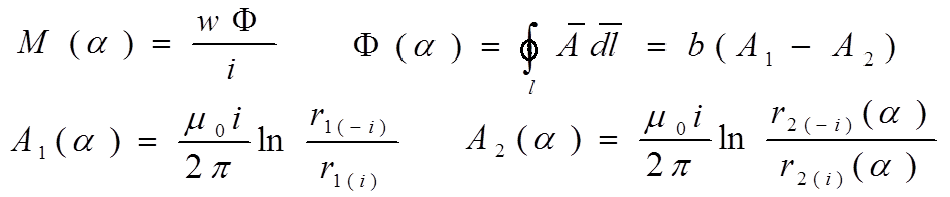
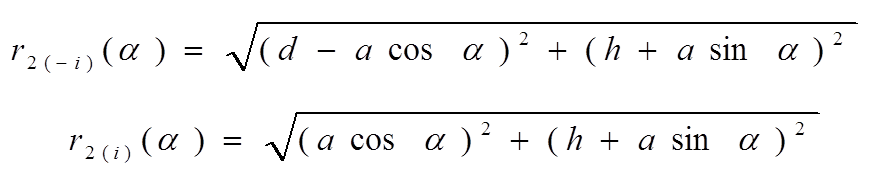
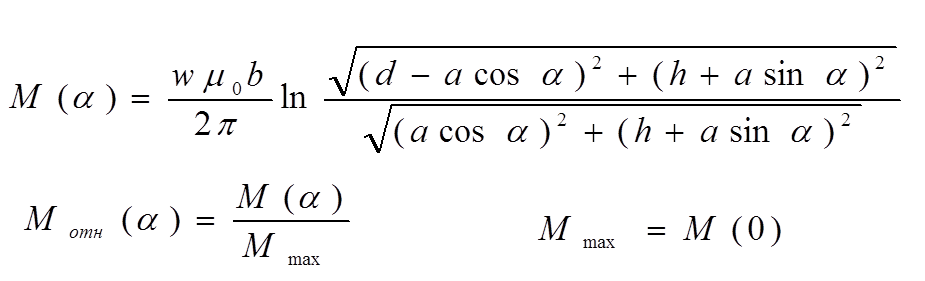
График распределения отностельного значения взаимной индуктивности от угла поворота рамки приведен ниже

Расчет проведен при заданных геометрических размерах:
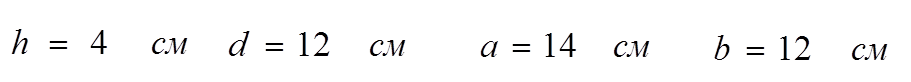
 2020-04-07
2020-04-07 521
521








