Общие сведение о работе усилителей бегущей волны в импульсном режиме

Приведенное выше рассмотрение выполнено для непреывногот режима усиления непрерывных сигналов. Ипульсный режим, т.е. режим, характерные времена которого меньше времени релаксации населенностей активной среды усилителя, требует отдельного анализа.

Пусть плоская волна падает на лазерный усилитель длиной l вдоль оси z. Уравнение переноса излучения в активной среде записывается в виде.

где I(z,t) – интенсивность излучения; t – время, z – координата, вдоль которой распространяется излучение; b – коэффициент нерезонансных потерь; a(I) – зависящий от интенсивности коэффициент усиления. В предыдущей лабораторной работе («Моделирование усилителя бегущей волны в стационарном режиме») рассматривался стационарный случай, когда интенсивность не меняется со временем и первый член в уравнении (1) равен нулю. Были рассмотрены три случая, когда интенсивность излучения много больше интенсивности насыщения, много меньше интенсивности насыщения, и соизмерима с интенсивностью насыщения. В первых двух случаях были получены простые аналитические формулы, в последнем случае было получено выражение, которое не имеет аналитического решения и решается численно. В данной работе рассмотрим импульсный режим, когда имеет место изменение интенсивности от времени, и первым членом в уравнении (1) пренебречь нельзя. Ограничимся рассмотрением случая, когда падающее излучение имеет вид импульса длительностью t_и, причем t₁ <<t_и<<t₂, где t₁ и t₂- времена жизни нижнего и верхнего уровней активной среды соответственно.

Рассмотрим 4-х уровневую схему. Для 4-х уровневой схемы 

Где D N  – инверсия заселенностей, W -вероятность соответствующего перехода

Интегрируя (1) по времени с использованием (2), получаем

Г_s – плотность энергии насыщения, a0 – линейный коэффициент усиления (коэффициент усиления слабого сигнала).

Проанализируем выражение (3). Рассмотрим три случая для различных диапазонов плотностей энергии:

1. Г << Гs.

В этом случае Г/Г_S <<1, т.е. Г/Г_S ®0. Тогда, используя свойство бесконечно малых функций e^x -1~ x при x ®0 и решая уравнение (3) в безразмерных переменных с начальным условием G(z=0)=G₀, получим G(z)=G₀exp[(a₀-b)z]. Таким образом, при малых уровнях сигнала наблюдается экспоненциальный рост выходной плотности энергии.

2. Г >> Гs.

В этом случае Г/Гs >> 1, и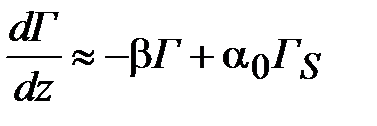

При значительных входных сигналах рост выходной плотности энергии замедляется и, начиная с некоторых значений, вообще прекращается. Стационарное значение выходной плотности энергии достигается, когда все, что может излучить единичный отрезок длины активного вещества в режиме полного насыщения, поглощается за счет нерезонансных потерь в том же отрезке. Этот баланс поглощенной и излученной энергий приводит к исчезновению дальнейшего усиления по мере распространения вдоль усилителя. Если плотность энергии достигает предельного значения Г пред, то это значит, что дальнейшего усиления нет и dГ/dz = 0. Тогда можем записать:  Отсюда получаем, . 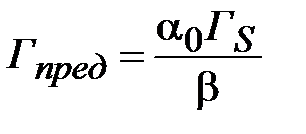Таким образом, в усилителе бегущей волны предельная выходная плотность энергии не зависит от входного сигнала, а определяется плотностью энергии насыщения, коэффициентом линейного усиления и коэффициентом нерезонансных потерь

3. Г ~ Гs

В этом случае уравение (3) не имеет аналитического решения и решается численно. Если пренебречь нерезонансными потерями в усилителе, можно получить аналитическое решение

Где G₀=exp(al) – ненасыщенное усиление усилителя, Г_вх – плотность энергии входного пучка.

3. Решение уравв среде Маткад

Введем безразмерную переменную G=Г/Г_S  . Тогда уравнение (3) можно переписать в виде

Уравнение (5) является однородным дифференциальным уравнением (ОДУ) первого порядка. Для нахождения распределения G вдоль оси распространения необходимо решить задачу Коши. Решение задачи Коши методом Рунге-
Кутта с помощью встроенной функции rkfixed описано в предыдущем разделе.