Достаточные условия потенциальности

Область  в пространстве называется односвязной, если любой замкнутый контур С, лежащий в области , можно непрерывным деформированием стянуть в точку, не выходя за пределы области.

Примеры:

Односвязные: сфера, куб, параллелепипед, шаровой слой (область между двумя вложенными друг в друга сферами).

Неодносвязные: тор.

Теорема. Если в односвязной области  поле  безвихревое, т.е. , то оно потенциально в этой области.

Нахождение потенциала.

Потенциал поля выражается интегралом .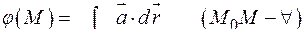

На практике берут  – начало координат, а путь  – ломанную кривую, состоящую из отрезков параллельных осям координат.

Пример: Найти потенциал:

(см. рис. 9.16)

1) Докажем, что поле  потенциально, т.е. :

Рис. 9.16

 

2)

 

9.7.2. Соленоидальное векторное поле

Определение: Векторное поле называется соленоидальным, если в любой точке , принадлежащей : .

Соленоидальным это поле назвали потому, что электрический ток, протекающий по соленоиду, создает магнитное поле, вектор напряженности которого имеет нулевую дивергенцию.

Соленоидальным является поле ротора любого векторного поля .

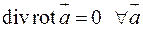
Свойство соленоидального поля.

Поток соленоидального поля через любую замкнутую поверхность 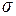, ограничивающую объем , равен нулю (из теоремы Гаусса-Остроградского):

.

 

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

 

1. Я.С.Бугров, С.М.Никольский. Высшая математика. Дифференциальное и интегральное исчисление. – М., Наука, 1980.

2. Л.Д.Кудрявцев. Курс математического анализа, т.1-2. – М., Высшая школа, 1981.

3. Л.Д.Кудрявцев, А.Д.Кутасов, В.И.Чехлов, М.И.Шабунин. Сборник задач по математическому анализу, т. 2-3. – М., Физматллит, 2003.

СОДЕРЖАНИЕ

ВВЕДЕНИЕ.. 3

1. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ.. 4

1.1. Первообразная, неопределенный интеграл. 4

1.2. Свойства неопределенного интеграла. 6

1.3. Таблица основных интегралов. 7

1.4. Методы интегрирования. 8

1.4.1. Интегрирование подстановкой. 8

1.4.2. Подведение под знак дифференциала. 9

1.4.3. Использование свойства линейности интеграла. 9

1.4.4. Интегрирование по частям. 9

2. ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ФУНКЦИЙ.. 11

2.1. Сведения из алгебры.. 11

2.2. Интегрирование рациональных функций. 14

2.3. Метод Остроградского. 17

2.4. Различные способы нахождения неопределенных коэффициентов 19

2.4.1 Метод частных значений. 19

2.4.2. Классический метод неопределенных коэффициентов. 20

2.4.3. Комбинированный метод. 20

3. ИНТЕГРИРОВАНИЕ НЕКОТОРЫХ КЛАССОВ ФУНКЦИЙ.. 21

3.1. Интегрирование тригонометрических выражений. 21

3.1.1. Универсальная тригонометрическая подстановка. 21

3.1.2. Интегралы от тригонометрических функций специального вида. 22

3.1.3. Интегрирование произведений степеней синусов и косинусов одинакового аргумента. 23

3.1.4. Интегрирование произведений синусов и косинусов кратных аргументов. 24

3.1.5. Тригонометрические подстановки в интегралах, содержащих корень квадратный из квадратного трехчлена. 24

3.1.6. Интегрирование выражений, содержащих иррациональности. 27

4. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ.. 32

4.1. Задача определения площади криволинейной трапеции. 32

4.2. Определенный интеграл как предел интегральной суммы.. 33

4.3. Теорема существования определенного интеграла. 34

4.4. Свойства определенного интеграла. 35

4.5. Интеграл с переменным верхним пределом.. 39

4.6. Формула Ньютона-Лейбница (основная теорема интегрального исчисления) 40

4.7. Замена переменной в определенном интеграле. 41

4.8. Формулы интегрирования по частям в определенном интеграле. 42

4.9. Геометрические приложения определенного интеграла. 43

4.9.1. Площадь плоской фигуры. 43

4.9.2. Площадь криволинейной трапеции. 44

4.9.3. Площадь криволинейных секторов и сегментов. 49

4.9.4. Длина дуги кривой. 51

4.9.5. Объем тела по известной площади поперечного сечения. 55

4.9.6. Объем тела вращения. 56

4.9.7. Площадь поверхности вращения. 58

5. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ... 59

5.1. Интегралы с бесконечными пределами. 60

5.1.1. Основные понятия. 60

5.1.2. Признаки сравнения. 61

5.1.3. Абсолютно и условно сходящиеся интегралы. 63

5.1.4. Теорема об абсолютной сходимости интегралов. 64

5.2. Интегралы от неограниченных функций. 64

5.2.1. Основные понятия. 64

5.2.2. Признак сравнения. 66

5.2.3. Интегралы смешанного типа. 66

6. КРАТНЫЕ ИНТЕГРАЛЫ... 67

6.1. Интеграл по области. 67

6.1.1. Мера ограниченной замкнутой области (фигуры). 67

6.1.2. Интеграл по фигуре. 68

6.1.3. Свойства интеграла по фигуре. 69

6.2. Двойной интеграл. 70

6.2.1. Определение, свойства и геометрический смысл двойного интеграла. 70

6.2.2. Вычисление двойного интеграла в декартовых координатах. 71

6.2.3. Геометрические и механические приложения двойного интеграла. 75

6.2.4. Двойной интеграл в криволинейных координатах. 77

6.3. Тройной интеграл. 85

6.3.1. Тройной интеграл: определение, свойства. 85

6.3.2. Тройной интеграл в декартовых координатах. 85

6.3.3. Тройной интеграл в криволинейных координатах. 87

6.3.4. Тройной интеграл в цилиндрических координатах. 88

6.3.5. Тройной интеграл в сферических координатах. 90

7. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ... 93

7.1. Криволинейный интеграл по длине дуги. 93

7.1.1. Определение криволинейного интеграла. 93

7.1.2. Вычисление криволинейного интеграла I-го рода (метод параметризации кривой). 94

7.2. Криволинейный интеграл II-го рода (интеграл по координатам) 96

7.2.1. Определение криволинейного интеграла по координатам. 96

7.2.2. Вычисление криволинейного интеграла по координатам. 98

7.3. Условия независимости криволинейного интеграла от пути интегрирования (на плоскости) 103

7.4. Приложение криволинейных интегралов. 106

8. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ... 107

8.1. Вычисление площади поверхности. 107

8.2. Поверхностные интегралы I-го рода. 111

8.2.1. Определение поверхностного интеграла I-го рода. 111

8.2.2. Вычисление поверхностного интеграла. 111

9. СКАЛЯРНЫЕ И ВЕКТОРНЫЕ ПОЛЯ.. 114

9.1. Скалярные поля. Основные понятия. 114

9.2. Связь вектора градиента с производной по направлению.. 118

9.3. Теорема об ортогональности вектора градиента поверхности уровня 119

9.4. Векторные поля. Основные понятия. 122

9.5. Поток векторного поля. 131

9.5.1. Поверхностный интеграл II-го рода. 131

9.5.2. Определение потока векторного поля. 132

9.5.3. Физический смысл потока векторного поля. 132

9.5.4. Вычисление потока. 133

9.5.5. Теорема Остроградского – Гаусса. 136

9.5.6. Физический смысл дивергенции. Источники и стоки. 141

9.6. Циркуляция векторного поля. 143

9.6.1. Основные понятия. 143

9.6.2. Формулировка Теоремы Стокса. 144

9.6.3. Инвариантность вектора ротора. 146

9.7. Специальные векторные поля. 147

9.7.1. Потенциальное поле. 147

9.7.2. Соленоидальное векторное поле. 150

БИБЛИОГРАФИЧЕСКИЙ СПИСОК.. 151

/