ЛЕКЦИИ ПО МАТЕМАТИЧЕСКОМУ АНАЛИЗУ
ИНТЕГРАЛЫ
УЧЕБНОЕ ПОСОБИЕ
МОСКВА 2013
ББК 22.161я73
Б 43
УДК 517(075)
Рецензенты: д.ф.-м.н. Г.А.Кабатянский
д.п.н. В.А.Лазарев
Б 43 Белецкая Н.В. Лекции по математическому анализу. Интегралы. Учебное пособие / Федеральное государственное бюджетное образовательное учреждение высшего профессиональ-ного образования «Московский государственный технический университет радиотехники, электроники и автоматики» – М., 2013. – 160 с.
В основу настоящего пособия положена вторая из четырех частей курса лекций по дисциплине «Математический анализ», который читается студентам дневного отделения МИРЭА. В пособии изложены следующие разделы математического анализа: неопределенный интеграл и методы его вычисления; определенный и несобственный интегралы, их геометрические приложения; кратные и криволинейные интегралы; скалярные и векторные поля. Рассматривается большое количество примеров и задач.
Ил. 78. Библиогр.: 3 назв.
Печатается по решению редакционно-издательского совета университета.
ISBN 978-5-7339-0894-6 с Н.В.Белецкая, 2013
с МГТУ МИРЭА, 2013
ВВЕДЕНИЕ
Курс лекций по математическому анализу имеет целью дать студентам базовые знания по одному из классических разделов математики, который является основой для многих математиче-ских и технических дисциплин, изучаемых ими в дальнейшем.
Настоящее пособие составлено на основе многолетнего опыта чтения курса лекций по математическому анализу автором – доцентом Н.В. Белецкой для студентов 1 – 2 курсов дневного отделения МИРЭА. Оно является вторым из четырёх планируемых пособий и отражает, соответственно, материал второго учебного семестра.
Базой для составления данного пособия явился конспект, записанный студентами в 2004 – 2006 г.г. и, как всякий конспект не претендовал на полноту изложения. В данном пособии некоторые разделы изложены более подробно, большинство теорем снабжены достаточно подробными доказательствами, вынужденно опущенными при чтении лекций.
Тематика разделов настоящего пособия дает представление о структуре курса. Условно он может быть разбит на следующие части: неопределенный интеграл и методы его вычисления; определенный и несобственный интегралы, их геометрические приложения; кратные и криволинейные интегралы; скалярные и векторные поля.
Теоретический материал иллюстрируется большим количеством практических задач с подробными решениями.
В списке литературы приведен перечень книг, которые рекомендуются к прочтению как для более полного усвоения предлагаемого курса, так и для углубленного изучения предмета, выходящего за рамки тематики конспекта.
Автор выражает надежду, что данное пособие поможет студентам в изучении курса математического анализа и будет признателен тем читателям, которые выскажут конструктивные замечания или укажут на имеющиеся опечатки.
1.1. Первообразная, неопределенный интеграл
Задачей дифференциального исчисления являлось нахождение производной или дифференциала данной функции. В интегральном исчислении решается обратная задача: по данной функции 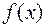 ищется такая функция
ищется такая функция 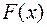 , чтобы
, чтобы 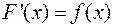 или
или 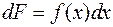 , т.е., другими словами, по данной производной или дифференциалу функции требуется восстановить эту функцию.
, т.е., другими словами, по данной производной или дифференциалу функции требуется восстановить эту функцию.
Примеры:
§ Пусть 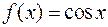 . Ясно, что эта функция есть производная от функции
. Ясно, что эта функция есть производная от функции 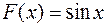 . Но верным будет и ответ
. Но верным будет и ответ 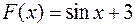 или
или 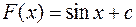 , где
, где 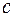 – любая действительная константа.
– любая действительная константа.
§ Пусть 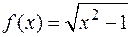 . В этом случае сразу ответить на вопрос, чему равна
. В этом случае сразу ответить на вопрос, чему равна 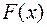 , непросто.
, непросто.
Определение 1.
Функция 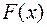 называется первообразной для функции
называется первообразной для функции 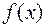 , определенной на интервале
, определенной на интервале 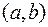 , если
, если 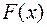 дифференцируема на
дифференцируема на 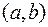 и
и 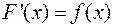 или
или 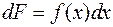 .
.
Замечание 1. Аналогично можно определить первообразную для функции, определенной на всей числовой оси 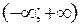 или на полупрямой, например
или на полупрямой, например 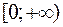 .
.
Замечание 2. Существование первообразной для данной функции не означает, что эта первообразная выражается в конечном виде через элементарные функции. Так, например, для функции 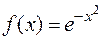 , непрерывной на всей числовой прямой, существует первообразная
, непрерывной на всей числовой прямой, существует первообразная 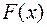 , так что
, так что 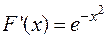 , однако
, однако 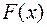 не может быть выражена комбинацией из конечного числа элементарных функций. Аналогично, это верно и для следующих функций:
не может быть выражена комбинацией из конечного числа элементарных функций. Аналогично, это верно и для следующих функций: 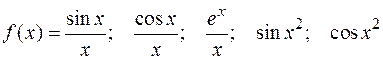 .
.
Из приведенного выше примера ясно, что если 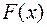 является первообразной для
является первообразной для 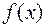 , то и функция
, то и функция 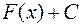 , где
, где 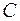 – произвольная постоянная, является первообразной для
– произвольная постоянная, является первообразной для 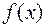 . Как же связаны между собой первообразные для одной и той же функции
. Как же связаны между собой первообразные для одной и той же функции 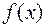 ? Ответ на этот вопрос дает:
? Ответ на этот вопрос дает:
Теорема о множестве первообразных.
Если функция 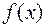 , определенная на интервале
, определенная на интервале 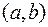 , имеет в данном интервале первообразную
, имеет в данном интервале первообразную 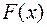 , то все первообразные выражаются формулой:
, то все первообразные выражаются формулой: 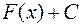 . Другими словами, любые две первообразные данной функции отличаются друг от друга на константу.
. Другими словами, любые две первообразные данной функции отличаются друг от друга на константу.
Доказательство:
Пусть 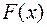 – первообразная для
– первообразная для 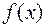 , т.е.
, т.е. 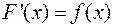 . Предположим, что существует другая первообразная
. Предположим, что существует другая первообразная 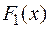 для
для 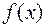 , т.е.
, т.е. 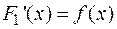 . Тогда
. Тогда 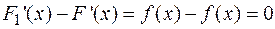 или
или 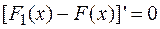 , следовательно,
, следовательно, 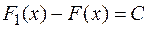 , т.е.
, т.е. 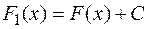 .
.
Определение 2.
Пусть 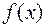 имеет в данном промежутке
имеет в данном промежутке 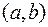 первообразную
первообразную 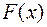 , так что
, так что 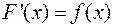 . Тогда
. Тогда 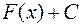 является одним выражением для всех первообразных, и называется неопределенным интегралом от данной функции
является одним выражением для всех первообразных, и называется неопределенным интегралом от данной функции 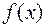 , что обозначается
, что обозначается
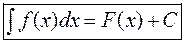
В этой формуле 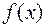 называется подынтегральной функцией, а
называется подынтегральной функцией, а 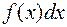 называется подынтегральным выражением.
называется подынтегральным выражением.
Важно понять, что неопределенный интеграл – это совокупность функций.
Так как действие интегрирования обратно по отношению к дифференцированию, то правильность интегрирования проверяется дифференцированием.
1.2. Свойства неопределенного интеграла
Прежде чем перейти к основным свойствам неопределенного интеграла, отметим (пока без доказательства) теорему о существовании первообразной, а, следовательно, и неопределенного интеграла у непрерывной функции.
Теорема о существовании первообразной и неопределенного интеграла у непрерывной функции.
Если функция 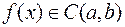 (непрерывна на интервале), то на
(непрерывна на интервале), то на 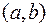 существует первообразная
существует первообразная 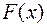 для данной функции и неопределенный интеграл.
для данной функции и неопределенный интеграл.
Из определения 2 вытекают следующие 2 свойства:
Свойство 1.
Тот факт, что 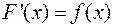 можно переписать в виде
можно переписать в виде 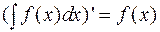 или, в дифференциалах, из условия, что
или, в дифференциалах, из условия, что 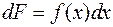 , следует, что
, следует, что 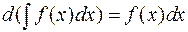 , т.е. производная от неопределенного интеграла равна подынтегральной функции, или дифференциал от интеграла равен подынтегральному выражению.
, т.е. производная от неопределенного интеграла равна подынтегральной функции, или дифференциал от интеграла равен подынтегральному выражению.
Свойство 2.
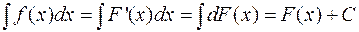 , т.е. интеграл от дифференциала функции равен этой функции плюс постоянная.
, т.е. интеграл от дифференциала функции равен этой функции плюс постоянная.
Эти два свойства означают, что стоящие рядом знаки  и d взаимно «сокращаются» (в последнем случае следует лишь добавить const).
и d взаимно «сокращаются» (в последнем случае следует лишь добавить const).
Отметим ещё одно важное свойство неопределенного интеграла.
Свойство 3. (свойство линейности неопределенного интеграла).
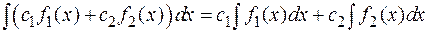 .
.
Это свойство проверяется дифференцированием левой и правой части равенства с использованием свойств линейности операции дифференцирования.
1.3. Таблица основных интегралов
Эта таблица получена как результат обращения таблицы производных основных элементарных функций.
1. 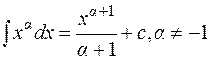 ;
; 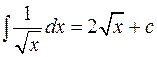 ;
; 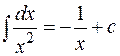
2. 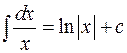 ;
; 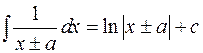
3. 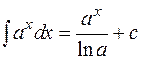 ;
; 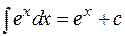 ;
; 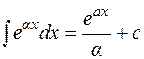
4. 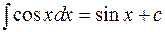 ;
; 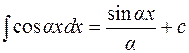
5. 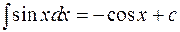 ;
; 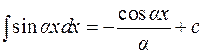
6. 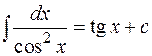
7. 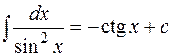
8. 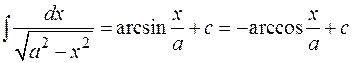
9. 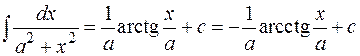
10. 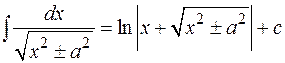 ,«длинный логарифм»
,«длинный логарифм»
11. 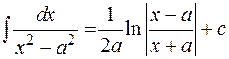 , «высокий логарифм»
, «высокий логарифм»
12. 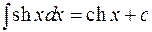
13. 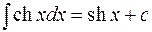
14. 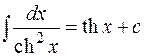
15. 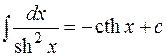
16. 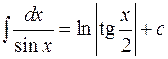
17. 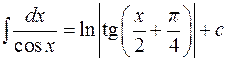
Пример:
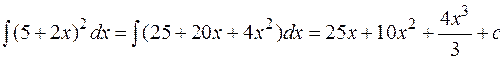 .
.
1.4.1. Интегрирование подстановкой
Пусть функция 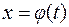 непрерывна и дифференцируема на некотором интервале, а функция
непрерывна и дифференцируема на некотором интервале, а функция 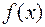 имеет первообразную
имеет первообразную 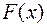 , т.е.
, т.е. 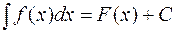 , тогда функция
, тогда функция 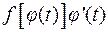 имеет первообразную
имеет первообразную 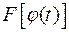 , т.е.:
, т.е.:
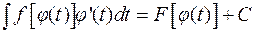 (1.1)
(1.1)
Доказательство формулы (1.1) непосредственно следует из правила дифференцирования сложной функции:
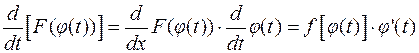 ,
,
т.е. функция 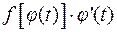 имеет своей первообразной функцию
имеет своей первообразной функцию 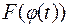 , что и доказывает формулу (1.1).
, что и доказывает формулу (1.1).
Пример:
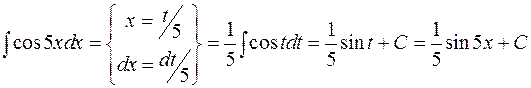 .
.
Часто бывает целесообразно применять подстановку в виде 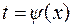 , где
, где 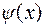 – дифференцируемая функция и
– дифференцируемая функция и 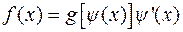 , причем функция
, причем функция 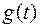 легко интегрируется, т.е. интеграл
легко интегрируется, т.е. интеграл 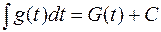 легко вычисляется. Тогда
легко вычисляется. Тогда 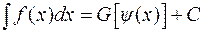 .
.
Пример:
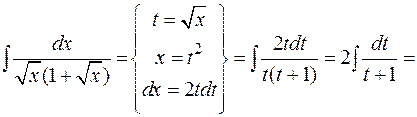
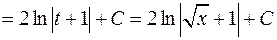 .
.
1.4.2. Подведение под знак дифференциала.
Непосредственно с методом подстановки связан прием, называемый подведением функции под дифференциал. Этот метод следует из формулы (1.1)
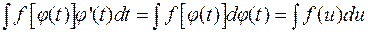 , который вычисляется.
, который вычисляется.
Пример:
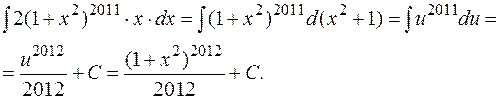
1.4.3. Использование свойства линейности интеграла.
Свойство линейности означает, что постоянные можно выносить за знак неопределённого интеграла, а интеграл от суммы функций равняется сумме интегралов от слагаемых.
Пример:
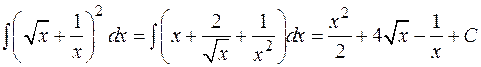 .
.
1.4.4. Интегрирование по частям.
Рассмотрим дифференцируемые функции  и
и 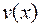 , тогда справедлива следующая формула:
, тогда справедлива следующая формула:
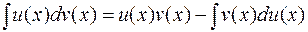 , (1.2)
, (1.2)
называемая формулой интегрирования по частям. Формулу (1.2) можно записать и по-другому:
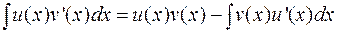 (1.2’)
(1.2’)
Докажем формулу (1.2). Для этого найдем дифференциал произведения 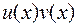 :
:
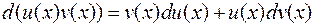
Проинтегрируем полученное равенство:
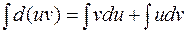 или
или 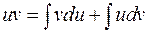 или
или 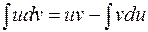 , ч.т.д.
, ч.т.д.
Эта формула сводит вычисление интеграла 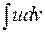 к вычислению интеграла
к вычислению интеграла 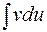 , который в ряде случаев вычисляется проще, чем первый. С помощью формулы (1.2) вычисляются интегралы, содержащие произведения функций, различных по своей природе. Например:
, который в ряде случаев вычисляется проще, чем первый. С помощью формулы (1.2) вычисляются интегралы, содержащие произведения функций, различных по своей природе. Например:
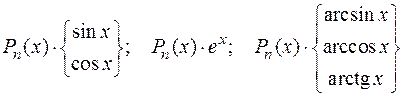 и т.п.
и т.п.
Примеры:
1)
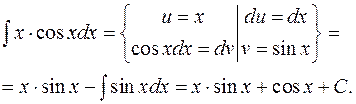
2)
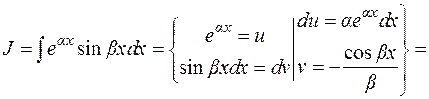
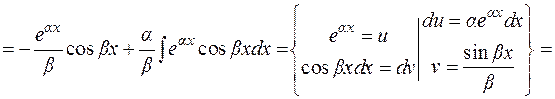
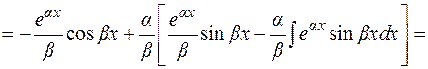
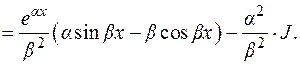
Отсюда 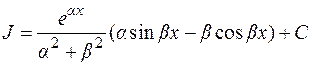 .
.
В примере 2 после повторного применения формулы (1.2) получается исходный интеграл с некоторым коэффициентом. Из полученного относительно 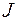 уравнения находим исходный интеграл. Подобным образом считаются интегралы
уравнения находим исходный интеграл. Подобным образом считаются интегралы 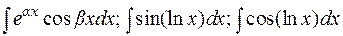 и другие.
и другие.
3) Примером на повторное применение формулы интегрирования по частям и возвращением к исходному интегралу может служить часто встречающийся интеграл 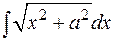 , который можно в дальнейшем отнести к табличным:
, который можно в дальнейшем отнести к табличным:
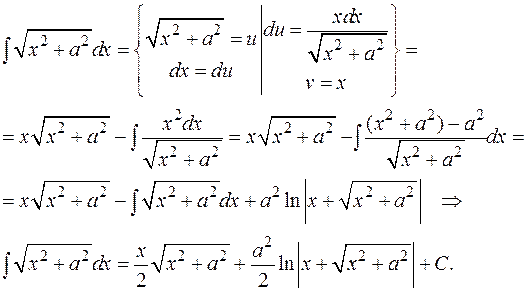
2. ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ФУНКЦИЙ
2.1. Сведения из алгебры
1. Всякий многочлен степени n
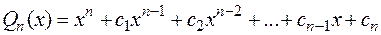 (2.1)
(2.1)
имеет ровно n корней в поле комплексных чисел, с учетом их кратности.
2. Если многочлен 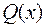 с действительными коэффициентами имеет комплексный корень
с действительными коэффициентами имеет комплексный корень 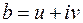 кратности β, то и сопряженное число
кратности β, то и сопряженное число 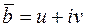 является корнем многочлена
является корнем многочлена 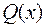 кратности β.
кратности β.
3. Любой многочлен 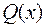 , имеющий действительные корни
, имеющий действительные корни 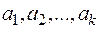 кратности
кратности 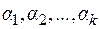 и комплексные корни
и комплексные корни 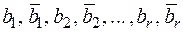 кратностей
кратностей 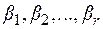 , может быть представлен в виде:
, может быть представлен в виде:
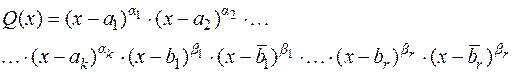
Т.к. 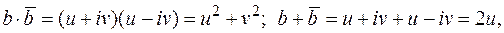
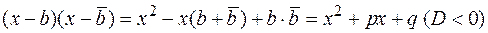 , где
, где 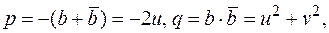 то
то 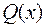 можно окончательно записать:
можно окончательно записать:
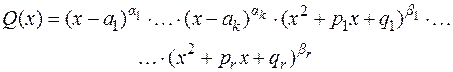 , (2.2)
, (2.2)
где 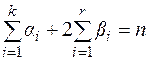 – степень
– степень 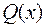 .
.
4. Любой приведенный квадратный трехчлен 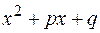 с комплексными корнями, т.е. с дискриминантом
с комплексными корнями, т.е. с дискриминантом 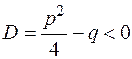 приводится к сумме квадратов, т.е.:
приводится к сумме квадратов, т.е.:
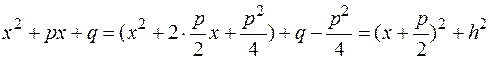 ,
,
где 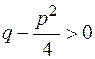 .
.
5. Любой многочлен  будем называть целой рациональной функцией. Дробно-рациональной функцией назовем отношение двух многочленов – т.е. функцию вида:
будем называть целой рациональной функцией. Дробно-рациональной функцией назовем отношение двух многочленов – т.е. функцию вида:
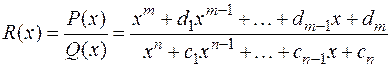 ,
,
причем дробно-рациональную функцию назовем правильной рациональной дробью, если 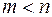 , и неправильной, если
, и неправильной, если 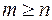 . Любую неправильную рациональную дробь можно представить в виде суммы целой функции и правильной дроби. Это достигается делением рационального числителя на знаменатель до тех пор, пока степень остатка не станет меньше степени знаменателя.
. Любую неправильную рациональную дробь можно представить в виде суммы целой функции и правильной дроби. Это достигается делением рационального числителя на знаменатель до тех пор, пока степень остатка не станет меньше степени знаменателя.
Пример:
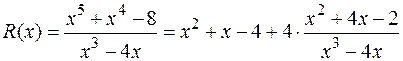
6. Простейшими дробями назовем дроби следующих четырех типов:
§ дробь I-го типа: 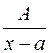 ;
;
§ дробь II-го типа: 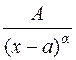 ;
;
§ дробь III-го типа: 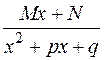 ;
;
§ дробь IV-го типа: 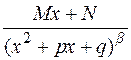 ;
;
где многочлен 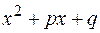 имеет комплексные корни, а
имеет комплексные корни, а  .
.
7. Теорема о разложении правильной рациональной дроби на сумму простейших дробей.
Любая правильная рациональная дробь 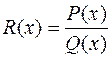 с вещественными коэффициентами и знаменателем вида (2.2) представляется, и единственным образом, в виде суммы простейших дробей:
с вещественными коэффициентами и знаменателем вида (2.2) представляется, и единственным образом, в виде суммы простейших дробей:
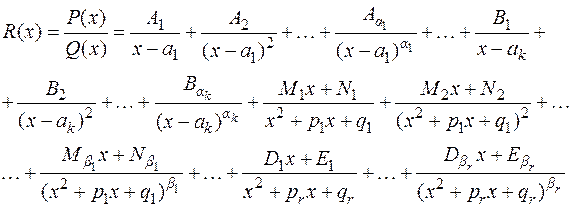
Пример:
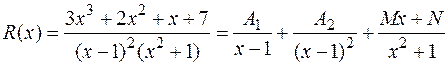
Коэффициенты найдем, приведя правую часть к общему знаменателю и применяя метод неопределенных коэффициентов, т.е. сравнивая числители полученных дробей и приравнивая коэффициенты при одинаковых степенях х:
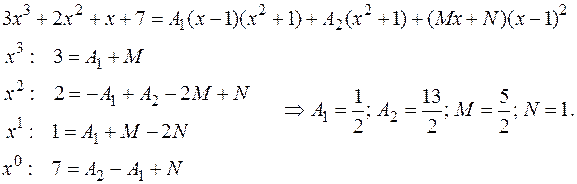
2.2. Интегрирование рациональных функций
1. Интегрирование целых рациональных функций производится по таблице интегралов, т.е.:
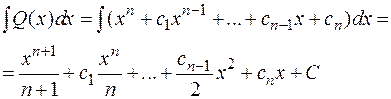
2. Интегрирование неправильной рациональной дроби сводится к интегрированию целой рациональной функции и правильной дроби. Всякая же правильная дробь согласно теореме представима в виде суммы простейших дробей, так что задача сводится к интегрированию простейших дробей. Рассмотрим интегрирование простейших дробей:
Дробь I типа: 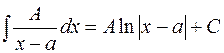 ;
;
Пример:
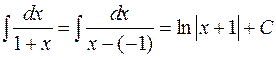
Дробь II типа: 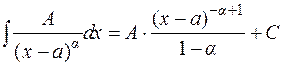 ;
;
Пример:
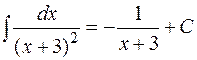
Более громоздкие вычисления придется провести в случае интегрирования дроби III-го типа:
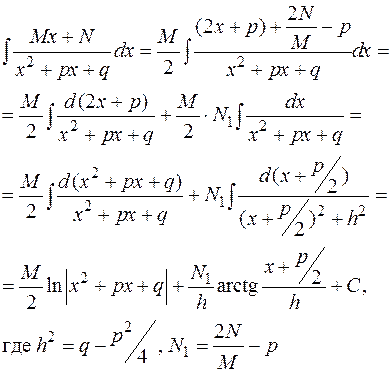
т.е. интегрирование дробей третьего типа сводится к выделению в числителе выражения, равного производной от знаменателя, и выделению полного квадрата в знаменателе. Интегрирование простейшей дроби III-го типа всегда дает линейную комбинацию логарифма и арктангенса.
Пример:
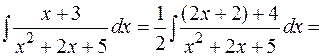
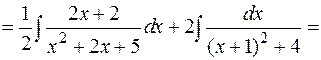
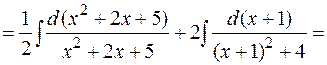
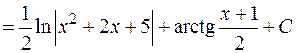 .
.
С дробью IV-го типа поступим следующим образом:
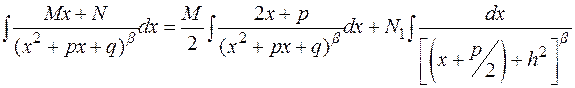
Первый из интегралов – табличный, второй же элементарными преобразованиями может быть приведен к виду
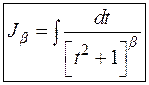 ,
,
который мы и проинтегрируем, используя уже известный метод интегрирования по частям:
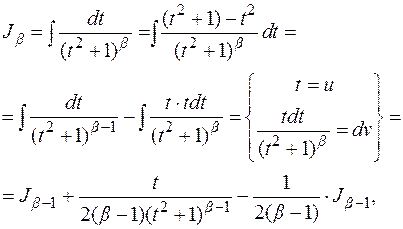
где 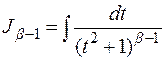
т.е. 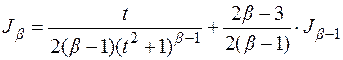
Получена рекуррентная формула, позволяющая понизить степень знаменателя. Последовательное применение этой формулы позволяет интеграл IV-го типа свести к интегралу от простейшей дроби III-го типа.
Итак, результатом интегрирования дробно-рациональных функций являются элементарные функции – 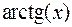 ,
, 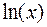 и рациональные функции.
и рациональные функции.
Пример:
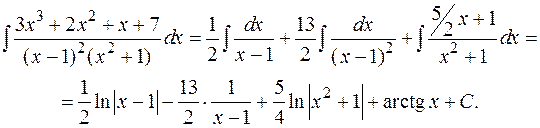
2.3. Метод Остроградского
Михаил Васильевич Остроградский (1801-1861) предложил остроумный способ интегрирования правильной рациональной дроби 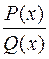 , удобный, когда знаменатель
, удобный, когда знаменатель 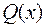 имеет кратные корни, особенно комплексные. Способ разложения на простейшие в этом случае связан с громоздкими выкладками.
имеет кратные корни, особенно комплексные. Способ разложения на простейшие в этом случае связан с громоздкими выкладками.
Отметим сначала, что при интегрировании дробей I и III типов получаем логарифмы и арктангенсы, т.е. нерациональные функции. Интеграл от дроби II-го типа есть правильная рациональная дробь, со знаменателем вида ( ) в степени (
) в степени ( ). Наконец, интеграл IV-го типа применением рекуррентных соотношений приводится к правильной рациональной дроби, со знаменателем, равным трехчлену
). Наконец, интеграл IV-го типа применением рекуррентных соотношений приводится к правильной рациональной дроби, со знаменателем, равным трехчлену 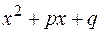 в степени (
в степени (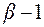 ) и интегралу типа
) и интегралу типа 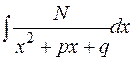 , приводящему к арктангенсу. После этого можно сделать вывод о том, чему будет равна рациональная часть интеграла от правильной рациональной дроби: это будет сумма правильных рациональных дробей со знаменателями:
, приводящему к арктангенсу. После этого можно сделать вывод о том, чему будет равна рациональная часть интеграла от правильной рациональной дроби: это будет сумма правильных рациональных дробей со знаменателями: 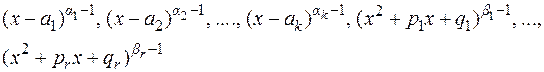 .
.
Указанная сумма будет правильной дробью 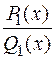 со знаменателем вида:
со знаменателем вида:
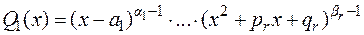 .
.
Сумма тех простейших дробей, интегралы от которых приводят к нерациональным функциям, будет правильной рациональной дробью 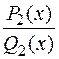 со знаменателем вида:
со знаменателем вида:
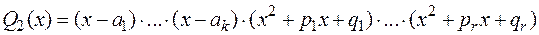 .
.
Таким образом, искомая формула Остроградского имеет следующий вид:
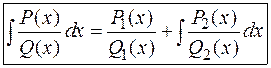
Для отыскания многочленов 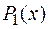 и
и 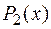 их записывают с неопределенными коэффициентами, которые находят дифференцированием формулы Остроградского.
их записывают с неопределенными коэффициентами, которые находят дифференцированием формулы Остроградского.
Пример:
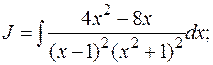
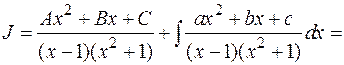
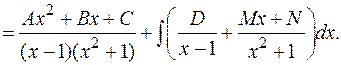
Продифференцируем обе части равенства:
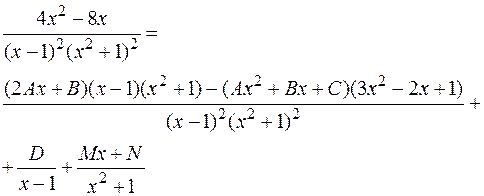
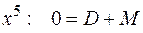
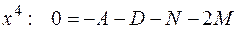
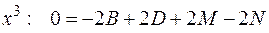
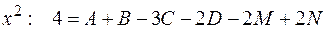
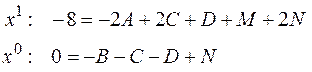
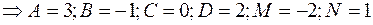
т.е. 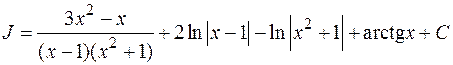
2.4. Различные способы нахождения неопределенных коэффициентов
2.4.1 Метод частных значений.
Этот метод разложения правильной дроби на простейшие удобно применять в том случае, когда корни знаменателя действительны и различны (кратности 1).
Пример:
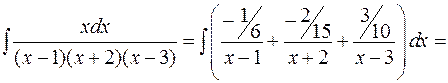
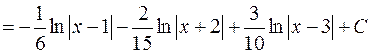
Коэффициенты находятся следующим образом:
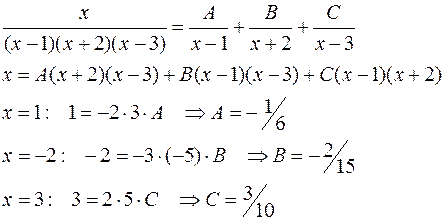
2.4.2. Классический метод неопределенных коэффициентов.Если среди корней знаменателя нет ни одного действительного, то можно воспользоваться сравнением коэффициентов при равных степенях переменной.
Пример:
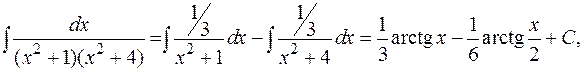
так как 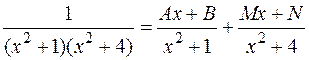
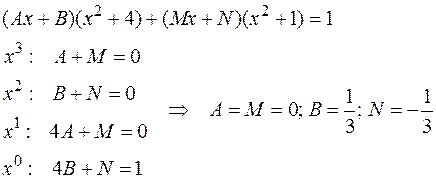
2.4.3. Комбинированный метод.Этот метод удобен, когда среди корней знаменателя есть хотя бы один действительный корень.
Пример:
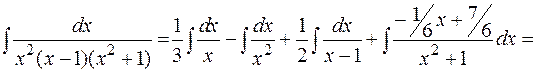
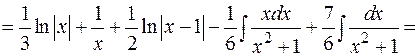
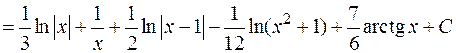 .
.
Подынтегральная функция разложена на простые дроби следующим образом:
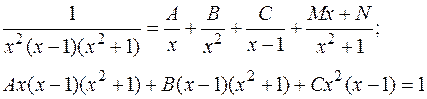
Применяя метод частных значений (п. 2.4.1), найдем B и C:
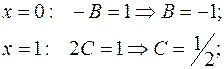
Остальные коэффициенты найдем, применяя классический метод неопределенных коэффициентов (см. п. 2.4.2):
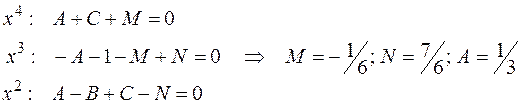 .
.
3. ИНТЕГРИРОВАНИЕ НЕКОТОРЫХ КЛАССОВ ФУНКЦИЙ
3.1. Интегрирование тригонометрических выражений
3.1.1. Универсальная тригонометрическая подстановка.
Пусть 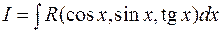 , R – рациональная функция. Введем переменную
, R – рациональная функция. Введем переменную 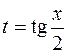 , выразим подынтегральное выражение через t, учитывая формулы тригонометрии:
, выразим подынтегральное выражение через t, учитывая формулы тригонометрии:
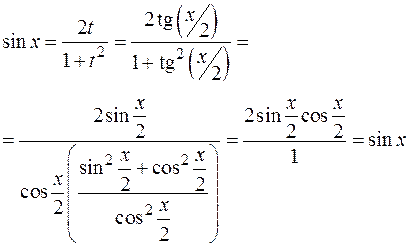
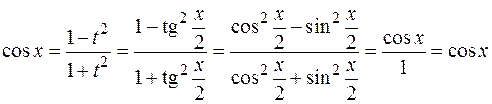
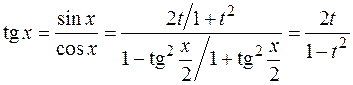
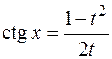
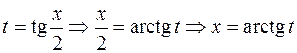
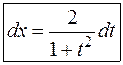
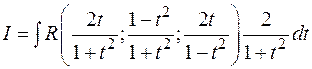
Пример:
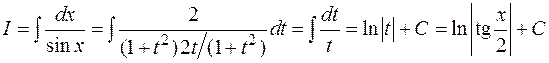
3.1.2. Интегралы от тригонометрических функций специального вида.
Интеграл вида 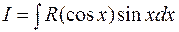 заменой
заменой 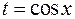 можно свести к интегрированию рациональной функции. Аналогично, для интеграла
можно свести к интегрированию рациональной функции. Аналогично, для интеграла 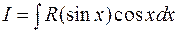 удобно применить замену
удобно применить замену 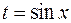 , а для интеграла
, а для интеграла 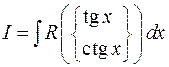 – замену
– замену 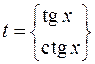 .
.
Пример:
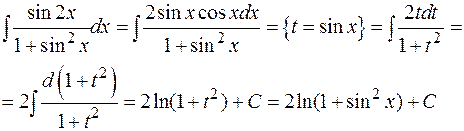
3.1.3. Интегрирование произведений степеней синусов и косинусов одинакового аргумента: 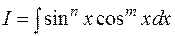
§ Если одно из чисел m или n – целое, нечетное, т.е. 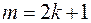 или
или 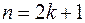 , то следует отделить тригонометрическую функцию в четной степени, а оставшуюся внести под знак дифференциала. Также нужно учитывать, что
, то следует отделить тригонометрическую функцию в четной степени, а оставшуюся внести под знак дифференциала. Также нужно учитывать, что 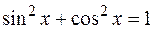
Пример:
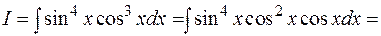
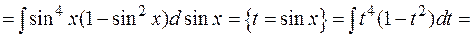
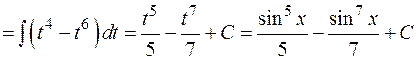
§ Если m и n – целые, четные, т.е. 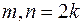 , то следует воспользоваться формулами понижения степени:
, то следует воспользоваться формулами понижения степени:
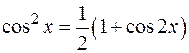
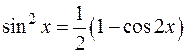
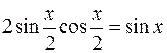
Пример:
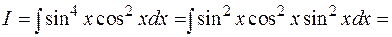
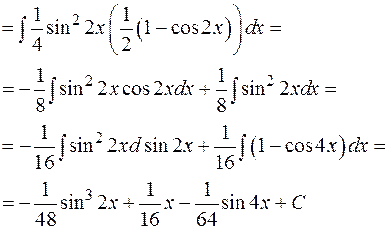
3.1.4. Интегрирование произведений синусов и косинусов кратных аргументов.
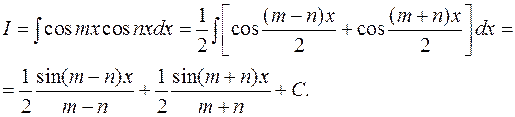
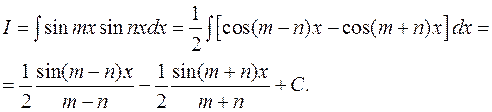
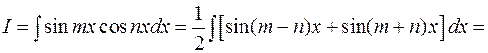
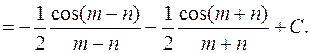
Пример:
Вычислить интеграл: 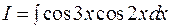
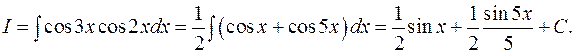
3.1.5. Тригонометрические подстановки в интегралах, содержащих корень квадратный из квадратного трехчлена.
Рассмотрим квадратный трехчлен 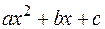 ,
, 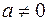 . Выделяя «полный квадрат», получим:
. Выделяя «полный квадрат», получим:
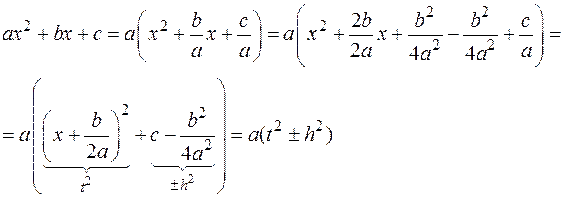
§ Если 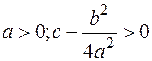 , то
, то 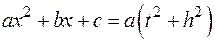
и интеграл 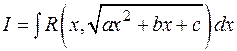 преобразуется к виду:
преобразуется к виду:
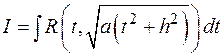
В этом случае удобно сделать замену: 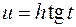 или
или 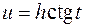 или
или 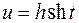 .
.
§ Если 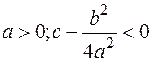 , то
, то 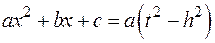
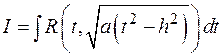
Сделать замену: 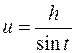 или
или 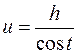 или
или 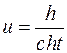 .
.
§ Если 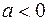 ;
; 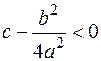 , то
, то 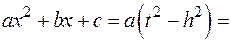
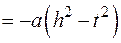
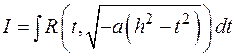
Сделать замену: 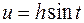 или
или 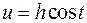 или
или 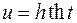 .
.
Примеры:
Вычислить интеграл:
1) 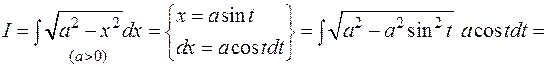
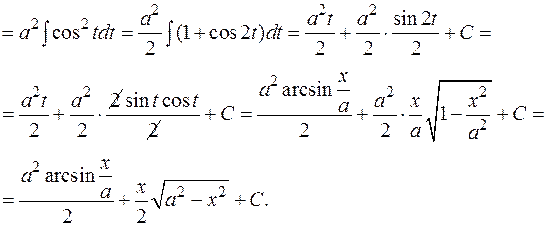
2) 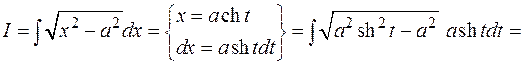
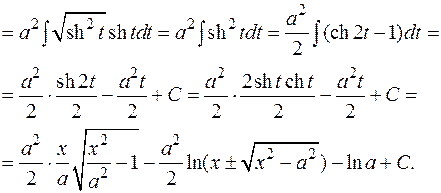
Переменная t найдена следующим образом:
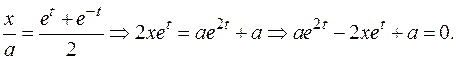 Решаем квадратное уравнение относительно
Решаем квадратное уравнение относительно 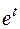 :
:
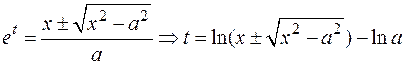
Окончательно 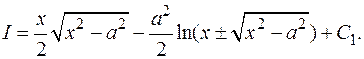
3) 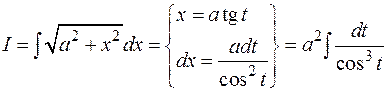
Такой заменой интеграл свёлся к интегралу от рациональной функции косинуса. Удобнее применить другую подстановку:
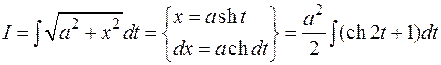
Действуя, как в предыдущем примере, получим:
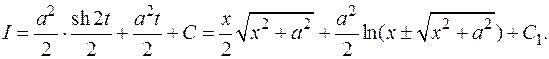
Замечание.
При интегрировании выражений, содержащих гиперболические функции, удобно пользоваться следующими формулами, которые в каком-то смысле являются аналогами тригонометрических:
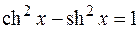 – гиперболическая единица.
– гиперболическая единица.
Сравните с 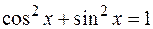 – тригонометрической единицей. А также сравните формулы понижения:
– тригонометрической единицей. А также сравните формулы понижения:
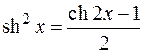 с
с 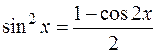 ,
,
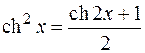 с
с 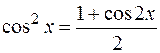 ,
,
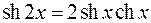 с
с 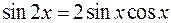 .
.
3.1.6. Интегрирование выражений, содержащих иррациональности.
Для интегралов, содержащих дробно-линейные иррациональности, ниже приведена рекомендуемая схема замен, приводящих подынтегральную функцию к рациональному виду.
Для 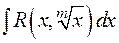 —
— 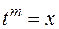 ,
,
для 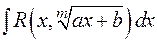 —
— 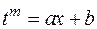 ,
,
для 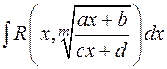 —
— 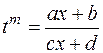 ,
,
для 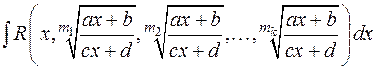 —
— 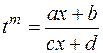 ,
,
где 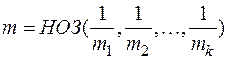 .
.
Примеры:
1)
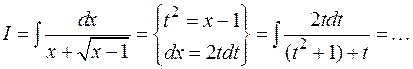
2)
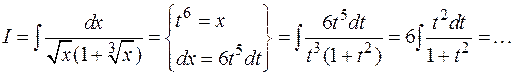
3)
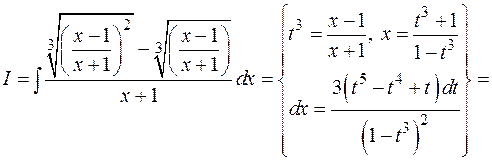
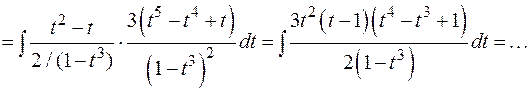
Во всех приведенных примерах осталось проинтегрировать рациональные дроби.
Перейдем к интегралам, связанным с квадратным корнем из квадратного трехчлена. Выше было показано, что выражение 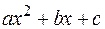 приводится к сумме или разности квадратов, поэтому интегралы вида
приводится к сумме или разности квадратов, поэтому интегралы вида
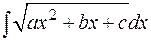 или
или 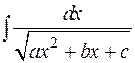
сводятся, соответственно, к
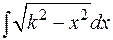
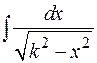
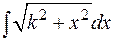 или
или 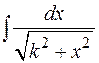 ,
,
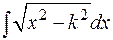
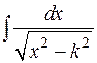
которые либо являются табличными, либо уже рассматривались.
Пример:
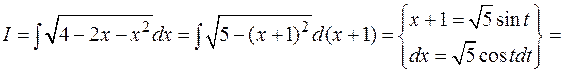
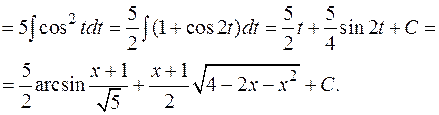
В интегралах вида 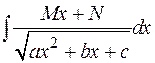 полезно в числителе выделить производную от подкоренного выражения.
полезно в числителе выделить производную от подкоренного выражения.
Пример:
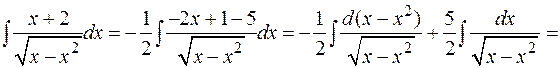
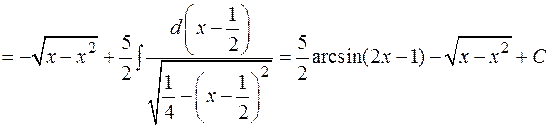 .
.
Интегралы вида 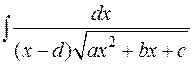 сводятся к рассмотренным случаям заменой
сводятся к рассмотренным случаям заменой 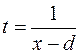 .
.
Пример:
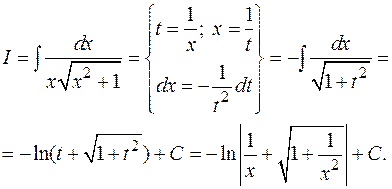
В интегралах вида 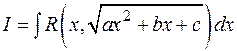 в некоторых частных случаях применяются так называемые подстановки Эйлера.
в некоторых частных случаях применяются так называемые подстановки Эйлера.
Если 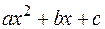
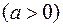 имеет комплексные корни, то замена
имеет комплексные корни, то замена 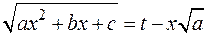 , называемая I-ой подстановкой Эйлера, сводит подынтегральное выражение к рациональному.
, называемая I-ой подстановкой Эйлера, сводит подынтегральное выражение к рациональному.
Действительно,
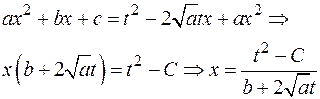
Подставим это выражение:
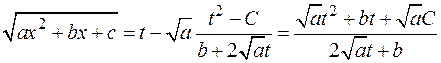
Теперь вычислим дифференциал
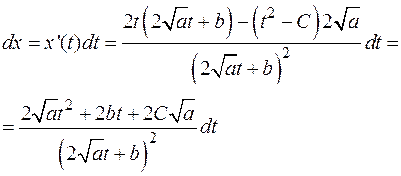
Тогда
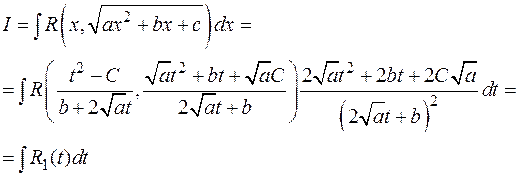
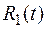 – рациональная функция от t.
– рациональная функция от t.
II-ая подстановка Эйлера 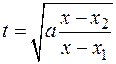 или
или 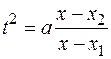 применяется, если
применяется, если 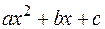 имеет различные вещественные корни
имеет различные вещественные корни 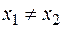 , то есть
, то есть
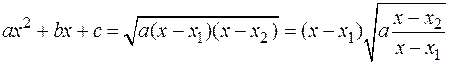 .
.
Пример:
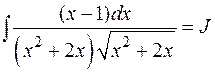 .
.
Так как 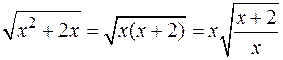 , сделаем подстановку
, сделаем подстановку 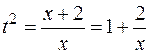 , тогда
, тогда 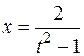 и
и 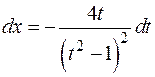 .
.
4.1. Задача определения площади криволинейной трапеции
Рассмотрим задачу о вычислении площади плоской фигуры, ограниченной плоской кривой 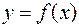 , определенной, непрерывной и неотрицательной на некотором отрезке
, определенной, непрерывной и неотрицательной на некотором отрезке 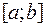 , ограниченной отрезком
, ограниченной отрезком 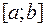 и прямыми
и прямыми 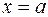 ,
, 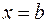 .
.
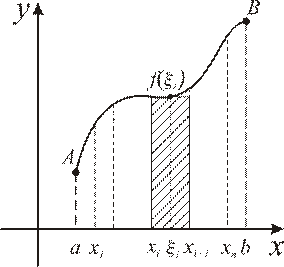
Рис. 4.1
Разобьем 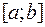 произвольным образом на n отрезков
произвольным образом на n отрезков 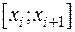 длины
длины 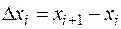 ,
, 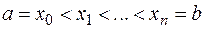 . На любом отрезке произвольно выберем точку
. На любом отрезке произвольно выберем точку 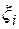 и на отрезке, как на основании, построим прямоугольник высотой
и на отрезке, как на основании, построим прямоугольник высотой 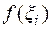 . Площадь одного такого прямоугольника равна
. Площадь одного такого прямоугольника равна 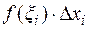 . Суммарная площадь всех построенных прямоугольников приблизительно будет равна искомой площади криволинейной трапеции aABb:
. Суммарная площадь всех построенных прямоугольников приблизительно будет равна искомой площади криволинейной трапеции aABb:
 (4.1)
(4.1)
Обозначим через 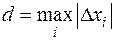 . Будем увеличивать число разбиений, одновременно устремляя
. Будем увеличивать число разбиений, одновременно устремляя 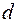 к нулю. Тогда сумма (4.1) будет все точнее выражать площадь криволинейной трапеции. Представляется естественным за искомую площадь принять предел суммы (4.1) при
к нулю. Тогда сумма (4.1) будет все точнее выражать площадь криволинейной трапеции. Представляется естественным за искомую площадь принять предел суммы (4.1) при 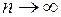 и
и 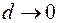 , т.е.:
, т.е.:
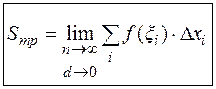 (4.2)
(4.2)
4.2. Определенный интеграл как предел интегральной суммы
Определение 1. Интегральная сумма.
Рассмотрим функцию 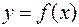 , определенную и непрерывную на
, определенную и непрерывную на 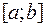 . Разобьем
. Разобьем 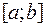 произвольным образом на n частей точками
произвольным образом на n частей точками 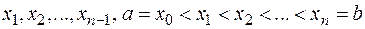 и на каждом полученном отрезке
и на каждом полученном отрезке 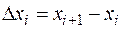 произвольно выберем точку
произвольно выберем точку 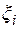 и вычислим значение функции в это точке. Составим сумму,
и вычислим значение функции в это точке. Составим сумму,
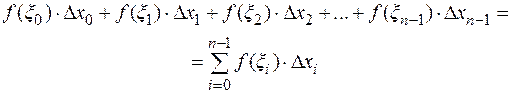 (4.3)
(4.3)
называемую интегральной суммой для функции 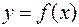 на отрезке
на отрезке 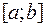 .
.
Определение 2. Разбиение отрезка.
Совокупность точек деления отрезка 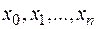 и промежуточных точек
и промежуточных точек 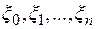 будем называть разбиением отрезка, и обозначать буквой Т.
будем называть разбиением отрезка, и обозначать буквой Т.
Каждому разбиению соответствует определенная интегральная сумма. Интегральная сумма есть функция, определенная на множестве разбиений.
Обозначим через 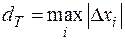 – диаметр разбиения. Устремим
– диаметр разбиения. Устремим 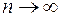 ,
, 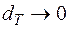 , тогда и все
, тогда и все 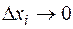 , и возьмем предел интегральной суммы (4.3):
, и возьмем предел интегральной суммы (4.3): 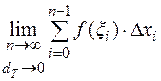
Определение 3. Определенный интеграл.
Определенным интегралом от функции 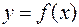 на отрезке
на отрезке 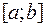 называется предел интегральной суммы (4.3) при
называется предел интегральной суммы (4.3) при 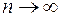 и
и 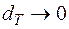 в предположении, что этот предел существует и не зависит от разбиения Т отрезка
в предположении, что этот предел существует и не зависит от разбиения Т отрезка 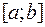 , т.е. от выбора точек
, т.е. от выбора точек 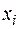 и
и 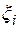 , что записывается так:
, что записывается так:
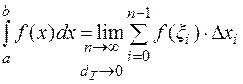 (4.4)
(4.4)
Очевидно, что определенный интеграл – это число (в отличие от неопределенного).
Определение 4. Интегрируемая функция.
Если у функции 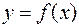 , определенной на отрезке
, определенной на отрезке 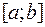 , существует определенный интеграл, то она называется интегрируемой на отрезке
, существует определенный интеграл, то она называется интегрируемой на отрезке 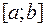 .
.
4.3. Теорема существования определенного интеграла
Напомним, что функция называется кусочно-непрерывной на 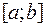 , если этот отрезок можно разбить на конечное число частей, на каждой из которых функция непрерывна. Теорема существования формулируется так:
, если этот отрезок можно разбить на конечное число частей, на каждой из которых функция непрерывна. Теорема существования формулируется так:
Если функция 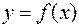 ограничена и кусочно-непрерывна на
ограничена и кусочно-непрерывна на 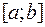 , то она интегрируема на этом отрезке.
, то она интегрируема на этом отрезке.
Следствие.
Интегрируемость непрерывной функции является частным случаем этой теоремы.
Приведем пример неинтегрируемой на отрезке 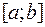 функции.
функции.
Пример:
Рассмотрим функцию Дирихле
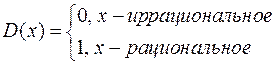
Выбираем произвольное разбиение отрезка 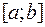 . В каждом
. В каждом  существует хотя бы одна рациональная точка. Если ее брать за
существует хотя бы одна рациональная точка. Если ее брать за 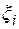 , то интегральная сумма будет равна
, то интегральная сумма будет равна 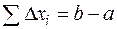 . На тех же
. На тех же  найдутся и иррациональные точки, тогда интегральная сумма, отвечающая данному выбору
найдутся и иррациональные точки, тогда интегральная сумма, отвечающая данному выбору 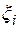 , будет равна нулю. В этом случае предел интегральной суммы не существует.
, будет равна нулю. В этом случае предел интегральной суммы не существует.
4.4. Свойства определенного интеграла
1. Если 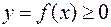 и
и 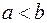 , то
, то 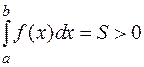 есть площадь криволинейной трапеции.
есть площадь криволинейной трапеции.
2. 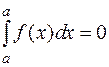 , т.к. все
, т.к. все  .
.
3. 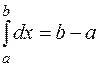 , т.к. интегральная сумма имеет вид
, т.к. интегральная сумма имеет вид 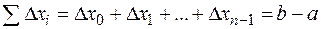 .
.
Интеграл от единицы равен длине отрезка интегрирования.
4. 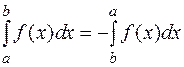 , т.к. все
, т.к. все 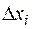 меняют знак, если разбиение отрезка начинать от точки b.
меняют знак, если разбиение отрезка начинать от точки b.
5. Свойство линейности определенного интеграла.
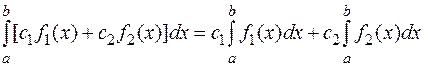 , если функции
, если функции 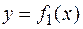 и
и 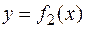 интегрируемы на
интегрируемы на 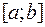 .
.
Доказательство:
Составим интегральную сумму для функции 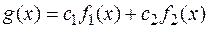 :
:
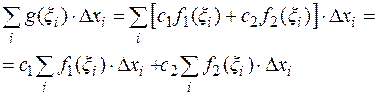 .
.
Переходя к пределу при
 и
и
|
|
 2020-04-12
2020-04-12 2414
2414