Если функция 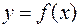 непрерывна на
непрерывна на 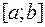 , то функция
, то функция 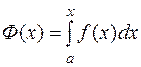 является первообразной для
является первообразной для 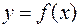 , т.е.
, т.е. 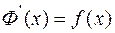 или, другими словами, производная интеграла с переменным верхним пределом по этому пределу равна подынтегральной функции.
или, другими словами, производная интеграла с переменным верхним пределом по этому пределу равна подынтегральной функции.
Доказательство:
Запишем приращение функции 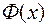 , используя формулу конечных приращений:
, используя формулу конечных приращений:
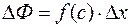 ,
, 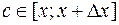 , тогда при
, тогда при 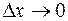
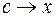 , т.е.
, т.е.
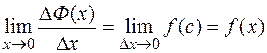 .
.
4.6. Формула Ньютона-Лейбница (основная теорема интегрального исчисления)
Формула устанавливает связь между первообразной функции 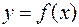 и определенным интегралом от этой функции.
и определенным интегралом от этой функции.
Основная теорема интегрального исчисления.
Если функция 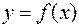 непрерывна на
непрерывна на 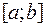 и
и 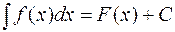 , то
, то
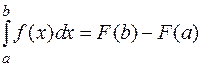 (4.9)
(4.9)
Доказательство:
Согласно предыдущей теореме у непрерывной функции 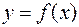 существует первообразная
существует первообразная 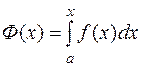 и, согласно условию, первообразная
и, согласно условию, первообразная 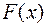 , отличающаяся от
, отличающаяся от 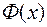 на константу:
на константу:
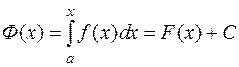 для
для 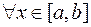
При х = а 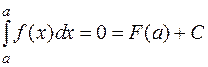 , т.е.
, т.е. 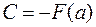 ,
,
При x = b 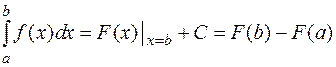 , ч.т.д.
, ч.т.д.
Пример:
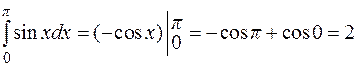
4.7. Замена переменной в определенном интеграле
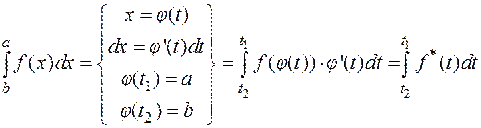 ,
,
где 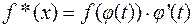 .
.
Пример:
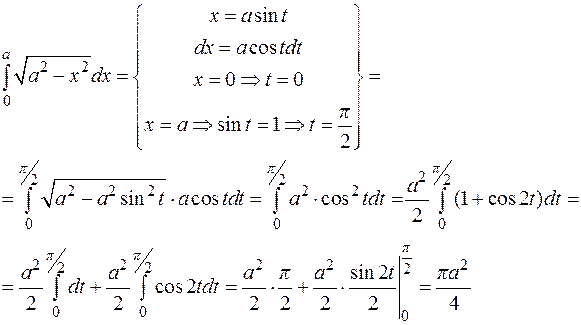
4.8. Формулы интегрирования по частям в определенном интеграле
Теорема.
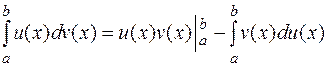
Доказательство:
Т.к. 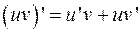 , т.е. функция
, т.е. функция 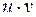 является первообразной для
является первообразной для 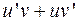 . Таким образом,
. Таким образом,
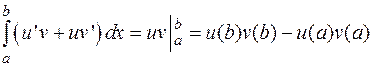
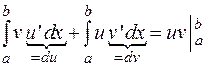
Пример:
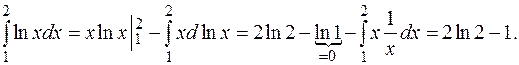
4.9. Геометрические приложения определенного интеграла
4.9.1. Площадь плоской фигуры.
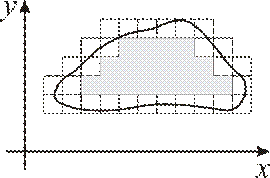
Рис. 4.4
Под площадью плоской фигуры будем понимать произвольное ограниченное множество точек на плоскости.
Напомним, что площадью прямоугольника называется произведение его основания на высоту. Это неотрицательное число, обладающее свойством аддитивности, т.е. если прямоугольник разбить на части прямыми, параллельными его сторонам, на меньшие прямоугольники, то площадь данного прямоугольника будет равна сумме площадей составляющих. Для произвольной плоской фигуры 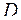 построим нижнее и верхнее приближение к искомой площади, т.е. две области, состоящие из прямоугольников:
построим нижнее и верхнее приближение к искомой площади, т.е. две области, состоящие из прямоугольников: 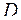 ex и
ex и 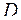 in – охватывающих
in – охватывающих 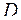 и содержащихся внутри
и содержащихся внутри 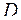 . Тогда искомая площадь S фигуры
. Тогда искомая площадь S фигуры 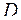 лежит:
лежит: 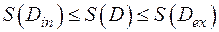 при любом выборе
при любом выборе 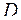 in и
in и 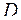 ex.
ex.
Продолжим разбиение прямоугольников прямыми, параллельными их сторонам, так, чтобы длины диагоналей всех прямоугольников стремились к нулю, тогда 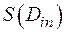 монотонно возрастает, а
монотонно возрастает, а 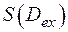 монотонно убывает.
монотонно убывает.
Плоская фигура 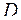 называется квадрируемой, если существует общий предел
называется квадрируемой, если существует общий предел 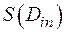 и
и 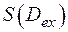 при неограниченном разбиении и при стремлении длин диагоналей прямоугольников к нулю. Этот общий предел и принимают за площадь S (
при неограниченном разбиении и при стремлении длин диагоналей прямоугольников к нулю. Этот общий предел и принимают за площадь S (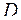 ). Естественно, что этот общий предел существует, когда
). Естественно, что этот общий предел существует, когда 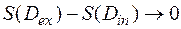 , т.е. когда граница области
, т.е. когда граница области  может быть заключена в кайму сколь угодно малой площади.
может быть заключена в кайму сколь угодно малой площади.
4.9.2. Площадь криволинейной трапеции.
Пусть функция 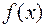 непрерывна и неотрицательна на отрезке
непрерывна и неотрицательна на отрезке 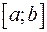 , то есть
, то есть 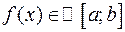 ,
, 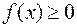 ,
, 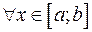 . Тогда площадь фигуры, ограниченной графиком функции
. Тогда площадь фигуры, ограниченной графиком функции 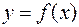 , осью абсцисс и двумя прямыми
, осью абсцисс и двумя прямыми 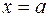 и
и 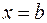 (см. рис. 4.5) определяется по формуле:
(см. рис. 4.5) определяется по формуле:
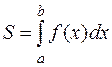
Пример:
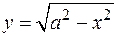 – полуокружность радиуса а с центром в точке О.
– полуокружность радиуса а с центром в точке О.
Другими словами:
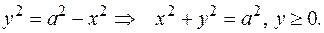
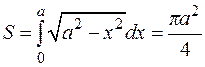
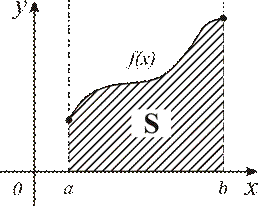
Известно, что площадь круга равна 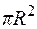 , где R – радиус круга, тогда площадь четверти круга равна
, где R – радиус круга, тогда площадь четверти круга равна 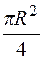 . И мы получили естественный результат при
. И мы получили естественный результат при 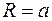 (см. рис. 4.6).
(см. рис. 4.6).
|
|
Если 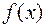 такова, что
такова, что 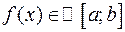 ,
, 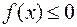 ,
, 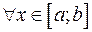 , (см. рис. 4.7), то тогда:
, (см. рис. 4.7), то тогда:
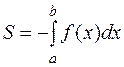

|
Если непрерывная, неотрицательная функция обладает свойством четности, т.е. определена для  и
и 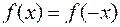 ,
, 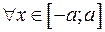 , то её график симметричен относительно оси ординат (см. рис. 4.8) и:
, то её график симметричен относительно оси ординат (см. рис. 4.8) и:
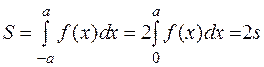
Если же функция 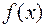 – нечетная, т.е. определена для
– нечетная, т.е. определена для  и
и 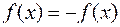 ,
, 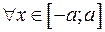 , то её график симметричен относительно начала координат (см. рис. 4.9) и по свойству аддитивности:
, то её график симметричен относительно начала координат (см. рис. 4.9) и по свойству аддитивности: 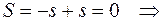
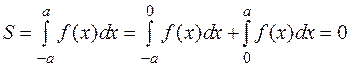 (см. рис. 4.9)
(см. рис. 4.9)
Пример:
Вычислить интеграл.
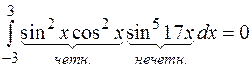 , так как подынтегральная функция нечетная, а интервал интегрирования симметричен.
, так как подынтегральная функция нечетная, а интервал интегрирования симметричен.
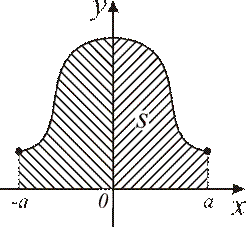
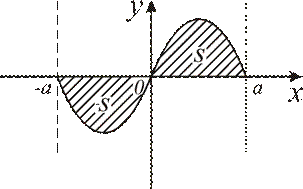
Рис. 4.8. Рис. 4.9.
Если искомая площадь заключена между графиками двух функций 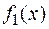 и
и 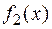 , причем
, причем 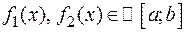 ;
; 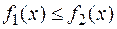 ,
, 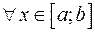 , (см. рис. 4.10), то
, (см. рис. 4.10), то
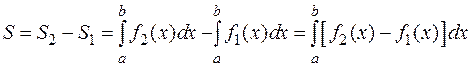 .
.

|
Пример:
Вычислить площадь фигуры, ограниченной прямой 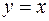 и параболой
и параболой 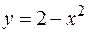 (см. рис. 4.11).
(см. рис. 4.11).
Решив уравнение 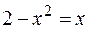 , найдем координаты точек пересечения прямой и параболы: А (-2; -2) и В (1; 1). Следовательно, искомая площадь равна:
, найдем координаты точек пересечения прямой и параболы: А (-2; -2) и В (1; 1). Следовательно, искомая площадь равна:
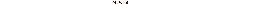
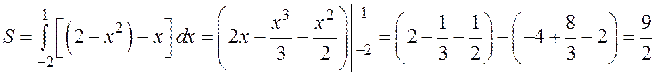 (ед2).
(ед2).

Если криволинейная трапеция ограничена кривой 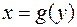 , определенной на отрезке
, определенной на отрезке 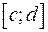 , и прямыми
, и прямыми 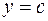 и
и 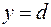 , т.е.
, т.е. 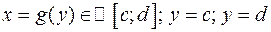 (см. рис. 4.12), то ее площадь вычисляется по формуле:
(см. рис. 4.12), то ее площадь вычисляется по формуле:

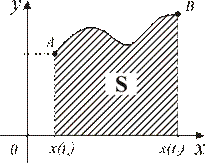
Рис. 4.13
Если кривая l, ограничивающая искомую площадь, задана параметрически, т.е. 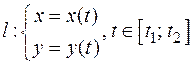 , причем
, причем 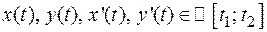 , т.е. функции
, т.е. функции 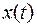 и
и 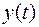 , а также их производные непрерывны на
, а также их производные непрерывны на 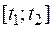 , так что параметру
, так что параметру 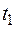 отвечает точка A, а
отвечает точка A, а 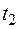 – точка В, т.е.
– точка В, т.е. 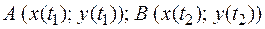 (см. рис. 4.13), то площадь такой трапеции вычисляется по формуле:
(см. рис. 4.13), то площадь такой трапеции вычисляется по формуле:
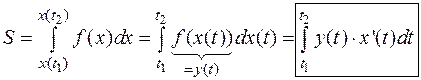
Пример:
Вычислить площадь фигуры, ограниченной одной аркой циклоиды: 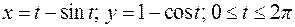 (см. рис. 4.14).
(см. рис. 4.14).
Искомая площадь будет равна:

Рис. 4.14
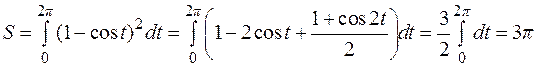 .
.
4.9.3. Площадь криволинейных секторов и сегментов.
Замечание: Известны формулы для вычисления площадей круга и кругового сектора (рис. 4.15):
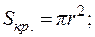
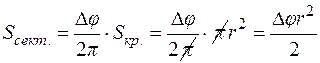

Рис. 4.15
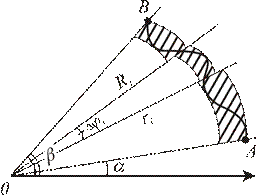
Рис. 4.16
Рассмотрим криволинейный сектор АОВ, как показано на рисунке 4.16., и поставим задачу определения его площади. Пусть искомая площадь, отнесенная к полярной системе координат, ограничена кривой 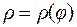 и лучами
и лучами 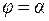 и
и 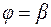 . Функцию
. Функцию 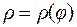 предположим непрерывной по
предположим непрерывной по 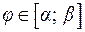 . Сектор АОВ разбиваем на n секторов с углами размаха
. Сектор АОВ разбиваем на n секторов с углами размаха 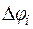 . Площадь каждого из них заменяем площадью кругового сектора радиуса
. Площадь каждого из них заменяем площадью кругового сектора радиуса 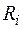 или
или 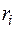 . Тогда площади вписанных и описанных фигур будут равны соответственно:
. Тогда площади вписанных и описанных фигур будут равны соответственно:
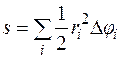 и
и 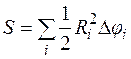 .
.
Если 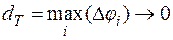 при
при 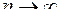 , то эти суммы стремятся к общему пределу, причем
, то эти суммы стремятся к общему пределу, причем 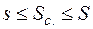 =>
=>
площадь криволинейного сектора равна:
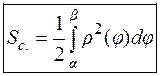
Пример:
Вычислить площадь фигуры, ограниченной одним витком архимедовой спирали и отрезком полярной оси: 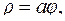 где
где 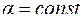 (см. рис. 4.17)
(см. рис. 4.17)

Рис. 4.17
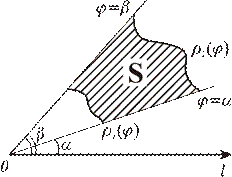
Рис. 4.18
Площадь криволинейного сегмента, ограниченного кривыми 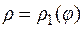 и
и 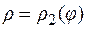 и лучами
и лучами 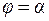 и
и 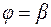 (рис. 4.18), можно вычислить по формуле:
(рис. 4.18), можно вычислить по формуле:
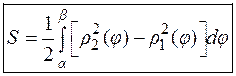
Пример:
Вычислить площадь, заключенную между линиями:
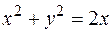 и
и 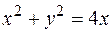 (см. рис 4.19)
(см. рис 4.19)
В полярных координатах указанные линии (окружности) имеют вид:
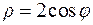 и
и 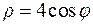
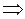
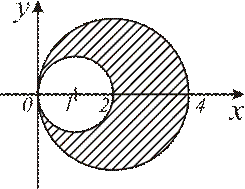
Рис. 4.19
4.9.4. Длина дуги кривой.
Пространственная кривая 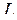 задается векторной функцией
задается векторной функцией 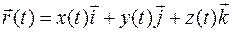 или тремя скалярными уравнениями:
или тремя скалярными уравнениями: 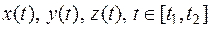 . Если эти три функции непрерывны на
. Если эти три функции непрерывны на 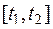 , то кривая
, то кривая 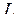 называется непрерывной. Если, кроме того, функции обладают непрерывными производными на
называется непрерывной. Если, кроме того, функции обладают непрерывными производными на 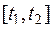 , то кривая
, то кривая 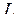 называется гладкой. Рассмотрим гладкую кривую
называется гладкой. Рассмотрим гладкую кривую 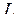 , заданную параметрически:
, заданную параметрически:
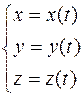 ,
,
где 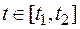 и значению
и значению 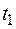 отвечает точка А – начало кривой
отвечает точка А – начало кривой 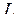 , а t2 – точка B – конец кривой
, а t2 – точка B – конец кривой 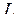 .
.
Разобьем кривую 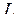 на n частей точками
на n частей точками 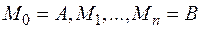 , точки
, точки 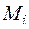 последовательно соединим ломанной, которая будет вписана в кривую
последовательно соединим ломанной, которая будет вписана в кривую 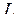 . Длиной кривой
. Длиной кривой 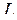 назовем предел периметра вписанной ломанной при неограниченном измельчении ее звеньев, а саму кривую
назовем предел периметра вписанной ломанной при неограниченном измельчении ее звеньев, а саму кривую 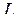 – спрямляемой. Вычислим периметр ломанной
– спрямляемой. Вычислим периметр ломанной 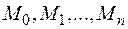 ; если каждой точке деления
; если каждой точке деления 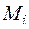 отвечает значение параметра
отвечает значение параметра 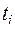 , то длина звена ломанной
, то длина звена ломанной 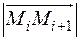 определяется по теореме Пифагора
определяется по теореме Пифагора
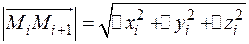 , где
, где
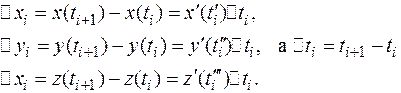
Тогда длина ломанной будет равна
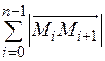
При измельчении ломанной, т.е. при  и
и  получим, что длина кривой
получим, что длина кривой 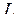 равна
равна
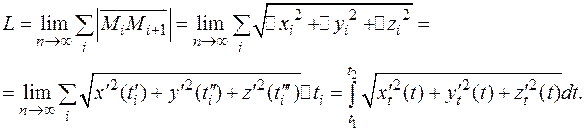 (4.6)
(4.6)
В частном случае плоской кривой в формуле (4.6) будет лишь отсутствовать третья координата.
Пример.
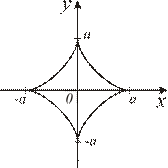
Рис. 4.20
Вычислить длину дуги астроиды (рис. 4.20):
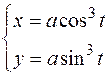
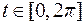
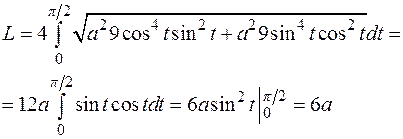 .
.
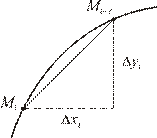
Рис. 4.21
В случае если дуга плоской кривой задана явно: 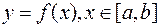 , то длина звена вписанной ломаной (рис. 4.21) определяется:
, то длина звена вписанной ломаной (рис. 4.21) определяется:
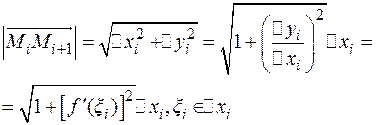
Тогда
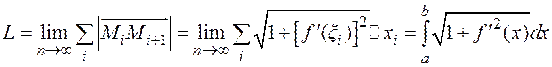 (4.7)
(4.7)
Пример:
Вычислить длину дуги полукубической параболы 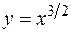 от точки А(0, 0) до точки В(4, 8)
от точки А(0, 0) до точки В(4, 8)
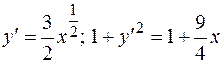
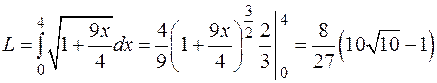
Если дуга плоской кривой задана в полярных координатах 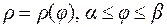 , то, переходя к декартовым координатам, получим:
, то, переходя к декартовым координатам, получим:
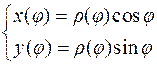 и подкоренное выражение в формуле (4.6) принимает вид:
и подкоренное выражение в формуле (4.6) принимает вид:
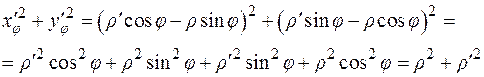
и формула длины дуги приобретает вид:
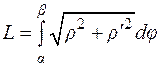 (4.8)
(4.8)
Пример:
Вычислить длину дуги кардиоиды.
Уравнение кардиоиды (см. рис. 4.22) имеет вид:
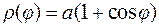 . Тогда
. Тогда 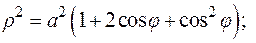
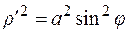 и
и 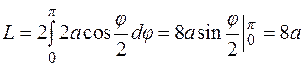 .
.
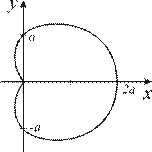
Рис. 4.22
Замечание: Рассмотрим дугу 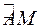 переменной длины (
переменной длины (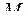 – текущая точка на дуге
– текущая точка на дуге 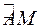 )
)
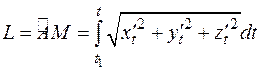 , тогда
, тогда
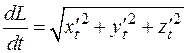 или
или
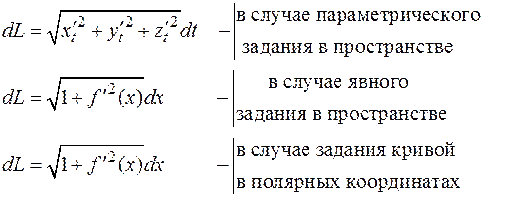 (4.9)
(4.9)
Выражение 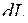 ,определяемое одной из формул (4.9) называется дифференциалом дуги.
,определяемое одной из формул (4.9) называется дифференциалом дуги.
4.9.5. Объем тела по известной площади поперечного сечения.
Пусть пространственное тело заключено между двумя плоскостями  и
и 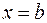 и в каждой точке
и в каждой точке 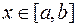 известна площадь
известна площадь 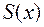 сечения тела плоскостью, перпендикулярной оси
сечения тела плоскостью, перпендикулярной оси 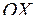 (рис. 4.23).
(рис. 4.23).
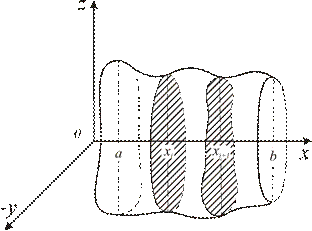
Рис. 4.23
Предположим, что функция 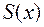 непрерывна по х. Вычислим объем этого тела. Разобьем отрезок
непрерывна по х. Вычислим объем этого тела. Разобьем отрезок 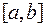 на n частей
на n частей 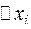 и через точки деления проведем плоскости
и через точки деления проведем плоскости 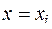 . Получим слои с известными площадями оснований и высотами, равными
. Получим слои с известными площадями оснований и высотами, равными 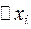 . Объем каждого из слоев
. Объем каждого из слоев 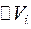 приближенно можно считать равным объему цилиндрического слоя:
приближенно можно считать равным объему цилиндрического слоя:
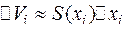
Тогда объем всего тела 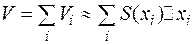 .
.
Эта интегральная сумма при 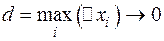 и
и 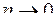 приведет к интегралу
приведет к интегралу
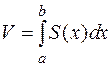 (4.10)
(4.10)
4.9.6. Объем тела вращения.
В частном случае, когда исследуемое тело является телом вращения, площадь каждого поперечного сечения есть круг. И если поверхность тела образована вращением дуги кривой 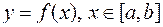 , то
, то 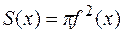 и формула (4.10) примет вид:
и формула (4.10) примет вид:
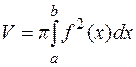 (4.11)
(4.11)
Примеры:
1. Найти объем, полученный от вращения синусоиды 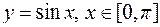 вокруг оси
вокруг оси 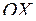 .
.
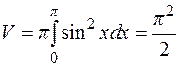 .
.
2. Найти объем эллипсоида 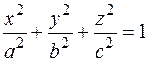 .
.
Часть эллипсоида, находящаяся в одном квадранте, изображена на рис. 4.24.
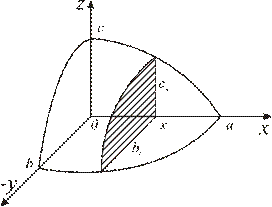
Рис. 4.24
Площадь эллипса равна 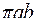 . Вычислим площадь сечения эллипсоида плоскостью
. Вычислим площадь сечения эллипсоида плоскостью 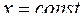 , т.е. площадь эллипса с полуосями
, т.е. площадь эллипса с полуосями 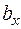 и
и 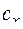 .
.
Полагая 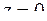 и
и 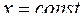 , получим:
, получим: 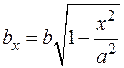 .
.
Полагая 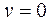 и
и 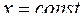 , найдем
, найдем 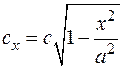 .
.
Площадь сечения 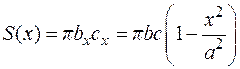 , тогда
, тогда
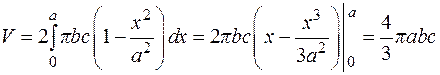 .
.
При 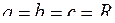 получаем известную формулу объема шара
получаем известную формулу объема шара 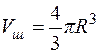 .
.
4.9.7. Площадь поверхности вращения.
Дуга 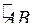 , заданная непрерывной с непрерывной производной функцией
, заданная непрерывной с непрерывной производной функцией 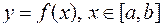 , вращается, например, вокруг оси
, вращается, например, вокруг оси 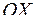 . Требуется определить площадь полученной поверхности вращения.
. Требуется определить площадь полученной поверхности вращения.
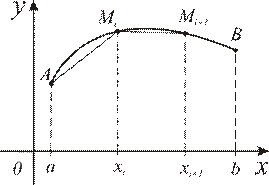
Рис.4.25
Разобьем 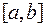 на n частей, получим отрезки
на n частей, получим отрезки 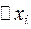 , в точках деления восстановим перпендикуляры до пересечения с дугой. Точки пересечения
, в точках деления восстановим перпендикуляры до пересечения с дугой. Точки пересечения 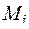 соединим ломаной. Звено ломаной при вращении описывает поверхность усеченного конуса с площадью
соединим ломаной. Звено ломаной при вращении описывает поверхность усеченного конуса с площадью 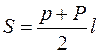 , где
, где 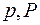 – периметры окружностей,
– периметры окружностей, 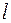 – длина образующей. В данном случае
– длина образующей. В данном случае
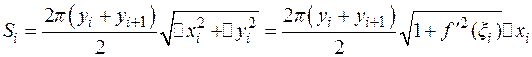 ; выражение
; выражение 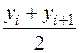 есть значение функции
есть значение функции 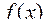 в некоторой точке
в некоторой точке 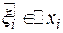 , тогда
, тогда
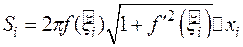
За площадь поверхности вращения примем предел этой интегральной суммы при 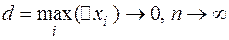 :
:
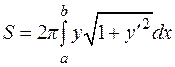 или (4.12)
или (4.12)
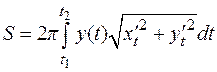 .
.
Пример:
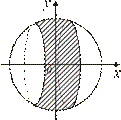
Рис. 4.26
Вычислить площадь шарового пояса, полученного при вращении вокруг оси  дуги окружности
дуги окружности 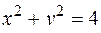 , лежащей между точками с абсциссами
, лежащей между точками с абсциссами  и
и 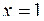 , как показано на рисунке 4.26.
, как показано на рисунке 4.26.
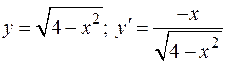 ;
;
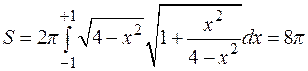 .
.
5. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
Изучение определенного интеграла проводилось в предположении: 1) о конечности отрезка интегрирования 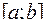 ; 2) об ограниченности интегрируемой функции
; 2) об ограниченности интегрируемой функции 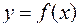 . Отказ от одного из этих допущений приведет нас к понятию несобственных интегралов с бесконечными пределами и несобственных интегралов от неограниченных функций.
. Отказ от одного из этих допущений приведет нас к понятию несобственных интегралов с бесконечными пределами и несобственных интегралов от неограниченных функций.
5.1. Интегралы с бесконечными пределами
5.1.1. Основные понятия.
Пусть функция 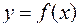 интегрируема на
интегрируема на 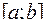 и непрерывна при
и непрерывна при 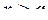 , тогда
, тогда
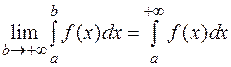 (5.1)
(5.1)
называется несобственным интегралом от функции у = f (x) с бесконечным верхним пределом (в предположении, что предел (5.1) существует). При этом интеграл (5.1) называется сходящимся. Если же предел (5.1) не существует или равен бесконечности, то несобственный интеграл называется расходящимся.
Геометрически сходимость интеграла (5.1) означает существование конечной площади под бесконечной кривой (рис. 5.1).
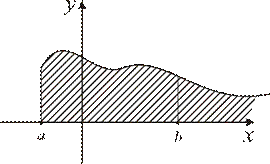
Рис. 5.1
Аналогично вводится понятие несобственного интеграла с бесконечным нижним пределом: 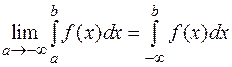 ,
,
или с двумя бесконечными пределами: 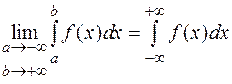 .
.
Здесь важно подчеркнуть, что интеграл определяется при независимом стремлении 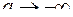 и
и 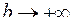 .
.
Из этих определений следует, что если при некотором значении а сходится каждый из интегралов: 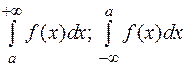 , то сходится и интеграл
, то сходится и интеграл 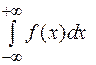 , причем
, причем 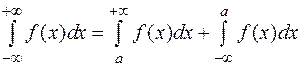 .
.
Примеры:
Исследовать на сходимость интегралы:
1. 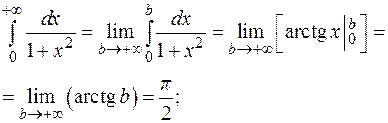
2. 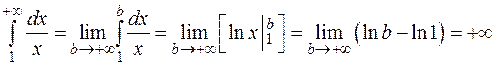
– интеграл расходится, так как предел бесконечен;
3. 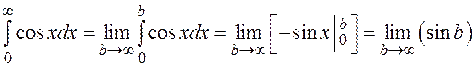 – интеграл расходится, так как такой предел не существует.
– интеграл расходится, так как такой предел не существует.
4. 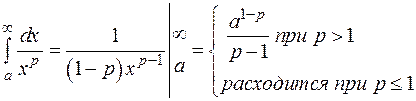
5.1.2. Признаки сравнения.
Теорема (I-й признак сравнения).
Если на полупрямой 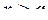 заданы две непрерывные функции
заданы две непрерывные функции 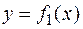 и
и 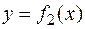 и для любого
и для любого 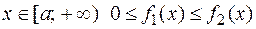 , то:
, то:
1. Если интеграл 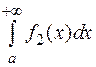 сходящийся, то и интеграл
сходящийся, то и интеграл 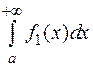 также сходящийся.
также сходящийся.
2. Если интеграл 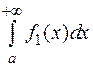 – расходящийся, то и интеграл
– расходящийся, то и интеграл 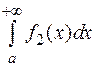 также расходящийся.
также расходящийся.
Доказательство:
Т.к. 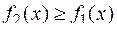 , то для любого
, то для любого 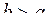 по свойствам определенного интеграла следует:
по свойствам определенного интеграла следует:
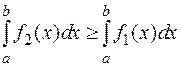 . Но интеграл
. Но интеграл 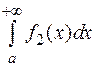 сходящийся, т.е.
сходящийся, т.е. 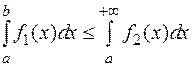 . Кроме того, с ростом b интеграл слева монотонно увеличивается, следовательно, существует
. Кроме того, с ростом b интеграл слева монотонно увеличивается, следовательно, существует 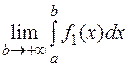 , т.е. интеграл
, т.е. интеграл 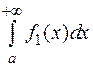 сходится.
сходится.
Второе утверждение является следствием доказанного.
Теорема (II-й признак сравнения).
Если на полупрямой 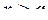 заданы две неотрицательные функции
заданы две неотрицательные функции 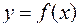 и
и 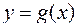 и существует конечный предел
и существует конечный предел 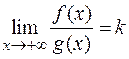 , причем
, причем 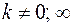 , то интегралы
, то интегралы 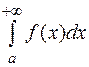 и
и 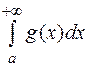 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Пример:
Исследовать на сходимость интегралы:
1. 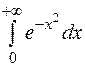 .
.
Сравним подынтегральную функцию с функцией 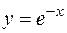 :
: 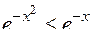 при х ≥ 1; интеграл
при х ≥ 1; интеграл 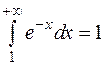 сходится, следовательно, сходится и исследуемый интеграл.
сходится, следовательно, сходится и исследуемый интеграл.
2. 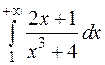 .
.
Сравним подынтегральную функцию с функцией 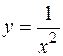 . Интеграл
. Интеграл 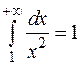 – сходится;
– сходится;
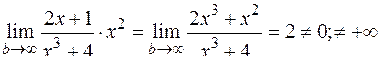 . Следовательно, исходный интеграл тоже сходится.
. Следовательно, исходный интеграл тоже сходится.
5.1.3. Абсолютно и условно сходящиеся интегралы.
Определение 1.
Интеграл 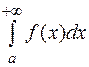 называется абсолютно сходящимся, если сходится интеграл
называется абсолютно сходящимся, если сходится интеграл 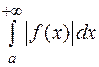 .
.
Определение 2.
Интеграл 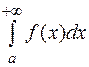 называется условно сходящимся, если сам интеграл сходится, а интеграл
называется условно сходящимся, если сам интеграл сходится, а интеграл 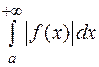 – расходится.
– расходится.
Пример:
1. Интеграл 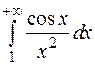 абсолютно сходящийся, т.к. сходится интеграл
абсолютно сходящийся, т.к. сходится интеграл 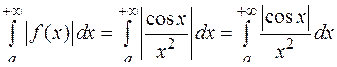 (т.к.
(т.к. 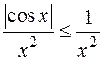 , а интеграл
, а интеграл 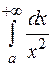 сходится, то отсюда следует сходимость интеграла
сходится, то отсюда следует сходимость интеграла 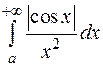 );
);
2. Интеграл 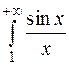 сходится условно, т.к. интеграл
сходится условно, т.к. интеграл 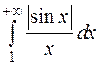 расходится, а сам интеграл, вычисленный по частям, дает:
расходится, а сам интеграл, вычисленный по частям, дает:
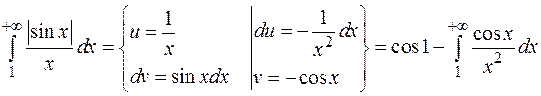 , являющийся сходящимся интегралом.
, являющийся сходящимся интегралом.
5.1.4. Теорема об абсолютной сходимости интегралов.
Если сходится интеграл 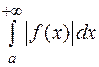 , то и интеграл
, то и интеграл 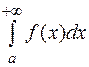 тоже сходится.
тоже сходится.
Действительно, 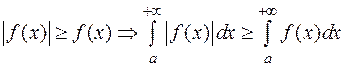 . Таким образом, применим I-й признак сравнения.
. Таким образом, применим I-й признак сравнения.
5.2. Интегралы от неограниченных функций
5.2.1. Основные понятия.
Пусть функция  определена на
определена на  и не ограниченна на нем, но ограничена на любом отрезке
и не ограниченна на нем, но ограничена на любом отрезке 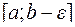 для любого положительного ε (рис. 5.2). Кроме того, функцию
для любого положительного ε (рис. 5.2). Кроме того, функцию 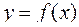 на этом полуинтервале будем предполагать интегрируемой, тогда по определению:
на этом полуинтервале будем предполагать интегрируемой, тогда по определению:
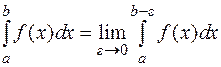 (5.2)
(5.2)
в предположении, что данный предел существует и конечен. В этом случае интеграл называется сходящимся. В противном случае интеграл – расходящийся.
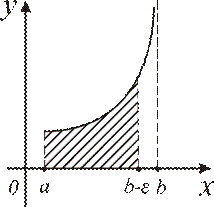
Рис. 5.2
Если же функция определена на 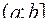 , то аналогично:
, то аналогично:
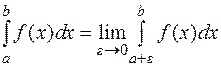 .
.
Пример:
1. 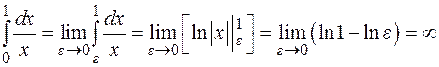 – интеграл расходится;
– интеграл расходится;
2. 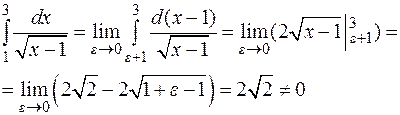 – интеграл сходится;
– интеграл сходится;
3.  Исследовать на сходимость в зависимости от параметра:
Исследовать на сходимость в зависимости от параметра:
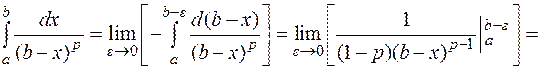
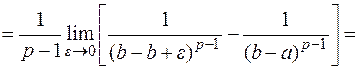
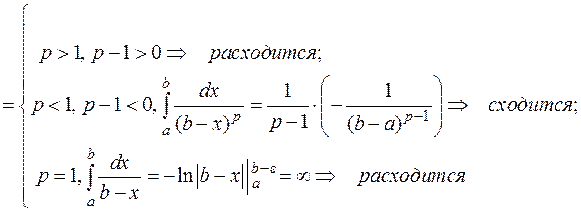
Замечание.
Если функция 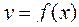 имеет разрыв II-го рода во внутренней точке с отрезка
имеет разрыв II-го рода во внутренней точке с отрезка 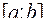 , то интеграл
, то интеграл 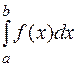 следует по свойству аддитивности разбить на два интеграла:
следует по свойству аддитивности разбить на два интеграла: 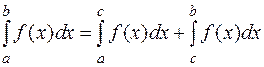 , и каждый из этих интегралов исследовать на сходимость.
, и каждый из этих интегралов исследовать на сходимость.
5.2.2. Признак сравнения.
Теорема.
Если на 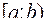 определены и непрерывны две функции, связанные неравенством
определены и непрерывны две функции, связанные неравенством 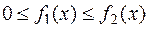 , и интеграл от большей функции сходится, то, следовательно, сходится и интеграл от меньшей функции. Аналогично, если интеграл от меньшей функции расходится, то расходится и интеграл от большей функции.
, и интеграл от большей функции сходится, то, следовательно, сходится и интеграл от меньшей функции. Аналогично, если интеграл от меньшей функции расходится, то расходится и интеграл от большей функции.
Аналогично, как и в п. 5.1.3, вводятся понятия абсолютной и условной сходимости для интеграла (5.2).
5.2.3. Интегралы смешанного типа.
На практике приходится встречать интегралы смешанного типа, у которых и пределы интегрирования бесконечны, и во внутренних точках интервала функция неограниченна.
Пример:
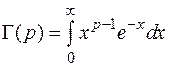 – гамма-функция, имеющая бесконечный верхний предел и разрыв II-го рода при
– гамма-функция, имеющая бесконечный верхний предел и разрыв II-го рода при 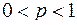 в точке
в точке  . Разобьем интеграл на две части:
. Разобьем интеграл на две части: 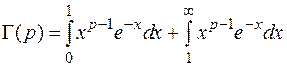 и исследуем каждый из них на сходимость. Результат: интеграл сходится при
и исследуем каждый из них на сходимость. Результат: интеграл сходится при 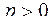 .
.
6. КРАТНЫЕ ИНТЕГРАЛЫ
6.1. Интеграл по области
6.1.1. Мера ограниченной замкнутой области (фигуры).
Самый общий процесс интегрирования имеет дело с некоторой определенной фигурой Ф некоторого пространства, причем «пространство» понимается в самом широком смысле: одномерное, двух-, трех-, n-мерное. Под фигурой соответственно понимается: в одномерном пространстве – отрезок прямой; в двухмерном – линия на плоскости, ограниченная область на плоскости; в трехмерном – пространственная линия, поверхность, объемное тело; в n-мерном – n-мерное тело.
В дальнейшем будет важно следующее: в рассматриваемом пространстве вводится понятие расстояния между любыми двумя точками пространства р1 и р2 как некоторого неотрицательного числа 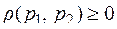 , обладающего свойствами:
, обладающего свойствами:
1. 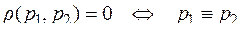 ;
;
2. 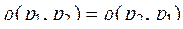 ;
;
3. 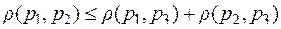 – аксиома «треугольника».
– аксиома «треугольника».
Кроме того, для любой рассматриваемой ограниченной фигуры Ф введем понятие меры, подразумевая под мерой отрезка, плоской или пространственной кривой их длину, под мерой плоской области или поверхности в пространстве будем понимать их площадь, а за меру пространственного тела примем его объем. Меру фигуры Ф будем обозначать так:
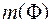 (6.1)
(6.1)
Введем еще одно понятие:
Диаметром фигуры Ф назовем наибольшее расстояние между точками фигуры, т.е.
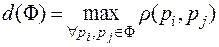 (6.2)
(6.2)
Пусть, кроме того, на фигуре Ф пространства распределена некоторая величина, которой приходится определенное количество на всякую часть фигуры Ф. Это может масса, электрический заряд, теплота, количество осадков и т.п. Т.к. при построении математических моделей физическая природа этой величины нам несущественна, то будем говорить, что в любой точке 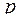 рассматриваемой фигуры Ф определена функция
рассматриваемой фигуры Ф определена функция 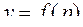 .
.
6.1.2. Интеграл по фигуре.
Рассмотрим задачу о вычислении массы М фигуры Ф с известной плотностью распределения массы 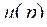 , т.е. с известной плотностью фигуры в любой точке р фигуры Ф.
, т.е. с известной плотностью фигуры в любой точке р фигуры Ф.
Для вычисления массы разобьем Ф на n непересекающихся частей: 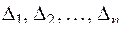 , так что
, так что 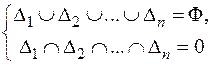
В каждой части 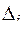 выберем точку
выберем точку 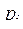 и предположим, что плотность во всех точках фигуры
и предположим, что плотность во всех точках фигуры 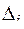 равна плотности в точке
равна плотности в точке 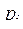 , т.е.
, т.е. 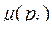 , тогда масса
, тогда масса 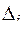 равна:
равна: 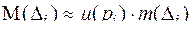 . Следовательно, масса всей фигуры Ф равна:
. Следовательно, масса всей фигуры Ф равна: 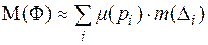 . Чем меньше фигуры
. Чем меньше фигуры 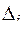 , тем полученная формула точнее.
, тем полученная формула точнее.
Перейдем теперь к введению понятия интегральной суммы и интеграла по фигуре Ф. Пусть на фигуре Ф определена функция y = f (p); разобьем фигуру Ф произвольным образом на части 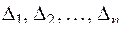 , на каждой из фигур
, на каждой из фигур 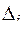 произвольно выберем точку рi и составим интегральную сумму:
произвольно выберем точку рi и составим интегральную сумму:
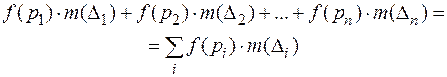 (6.3)
(6.3)
называемую интегральной суммой для функции 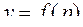 по фигуре Ф. Продолжим разбиение фигуры Ф, предполагая, что
по фигуре Ф. Продолжим разбиение фигуры Ф, предполагая, что 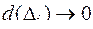 и перейдем к пределу, предположив, что такой предел интегральной суммы существует, не зависит от способа разбиения фигуры Ф и выбора точек
и перейдем к пределу, предположив, что такой предел интегральной суммы существует, не зависит от способа разбиения фигуры Ф и выбора точек 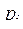 в каждой фигуре
в каждой фигуре 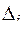 , тогда
, тогда
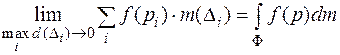 (6.4)
(6.4)
назовем интегралом по фигуре (области) Ф от функции 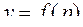 .
.
Теорема о существовании интеграла по фигуре.
Если функция 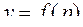 непрерывна на фигуре Ф, то предел (6.4) существует и функция
непрерывна на фигуре Ф, то предел (6.4) существует и функция 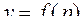 интегрируема.
интегрируема.
6.1.3. Свойства интеграла по фигуре.
1) линейность:
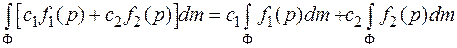
Это свойство следует из определения интеграла как предела интегральной суммы.
2) аддитивность:
если 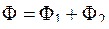 и
и 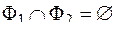 , то
, то 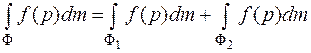
Доказательство основывается на рассуждениях, аналогичных доказательству этого свойства для определенного интеграла.
3) Если функции 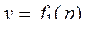 и
и 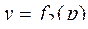 интегрируемы на фигуре Ф и для любой точки р, принадлежащей фигуре Ф, выполняется неравенство
интегрируемы на фигуре Ф и для любой точки р, принадлежащей фигуре Ф, выполняется неравенство 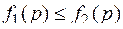 , то
, то
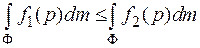 (6.5)
(6.5)
4) Теорема об оценке интеграла по фигуре:
Если 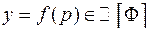 , то
, то
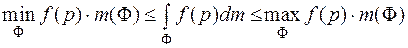 (6.6)
(6.6)
Доказательство опирается на формулу (6.4), линейность, а также на то, что
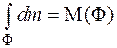 (6.7)
(6.7)
5) Теорема о среднем для интеграла по фигуре:
Если 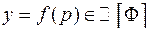 , то, следовательно, существует такая точка
, то, следовательно, существует такая точка 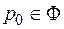 , что
, что
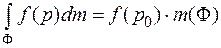 (6.8)
(6.8)
6.2. Двойной интеграл
6.2.1. Определение, свойства и геометрический смысл двойного интеграла.
Рассмотрим случай, когда фигура Ф есть плоская область 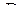 , замкнутая и ограниченная. В этой области задана функция
, замкнутая и ограниченная. В этой области задана функция 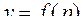 . Мерой плоской области будет ее площадь S (
. Мерой плоской области будет ее площадь S (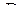 ). Разбиение области
). Разбиение области 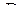 на части
на части 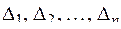 , выбор в любой
, выбор в любой 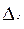 точек
точек 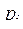 , составление интегральной суммы
, составление интегральной суммы 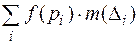 и переход к пределу при
и переход к пределу при 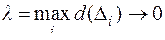 приводит к частному случаю интеграла по фигуре, а именно, к двойному интегралу от функции
приводит к частному случаю интеграла по фигуре, а именно, к двойному интегралу от функции 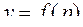 по плоской области
по плоской области 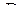 :
:
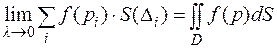 (6.9)
(6.9)
Для двойного интеграла справедливы все свойства, выведенные для интеграла по фигуре. Например: 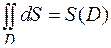 , а теорема о среднем для двойного интеграла имеет вид:
, а теорема о среднем для двойного интеграла имеет вид: 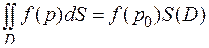 .
.
Выясним геометрический смысл двойного интеграла. Поместим плоскую область 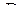 на плоскость хOу. Тогда функция
на плоскость хOу. Тогда функция 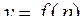 , определенная на плоской области
, определенная на плоской области 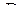 , геометрически представляет собой некоторую поверхность в пространстве:
, геометрически представляет собой некоторую поверхность в пространстве: 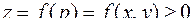 . Разобьем плоскую область
. Разобьем плоскую область 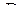 на
на 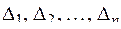 и выберем на каждой площадке
и выберем на каждой площадке 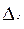 точку рi. Значение функции
точку рi. Значение функции 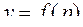 есть аппликата точки, лежащей на поверхности
есть аппликата точки, лежащей на поверхности 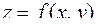 . Каждое слагаемое, стоящее в интегральной сумме (5.4.1)
. Каждое слагаемое, стоящее в интегральной сумме (5.4.1) 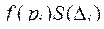 геометрически представляет собой объем прямой призмы высотой
геометрически представляет собой объем прямой призмы высотой 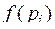 и площадью основания
и площадью основания 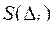 . Интегральная сумма есть сумма объемов соответствующих прямых призм, стоящих на площадках
. Интегральная сумма есть сумма объемов соответствующих прямых призм, стоящих на площадках  . Предел этой суммы, т.е. двойной интеграл геометрически представляет собой объем призмы, в основании которой лежит область
. Предел этой суммы, т.е. двойной интеграл геометрически представляет собой объем призмы, в основании которой лежит область 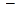 , ограниченной сверху поверхностью
, ограниченной сверху поверхностью 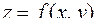 и боковой поверхностью с образующей параллельной оси 0 z. Таким образом, с помощью двойных интегралов можно вычислять объемы.
и боковой поверхностью с образующей параллельной оси 0 z. Таким образом, с помощью двойных интегралов можно вычислять объемы.
6.2.2. Вычисление двойного интеграла в декартовых координатах.
Вычисление двойного интеграла обычно сводится к вычислению двух определенных интегралов. Так как разбиение области 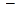 можно проводить произвольным образом, то будем разбивать
можно проводить произвольным образом, то будем разбивать 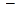 на площадки
на площадки 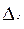 прямыми, параллельными осям 0 х и 0 y, тогда площадь
прямыми, параллельными осям 0 х и 0 y, тогда площадь 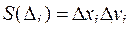 и элемент площади в интеграле
и элемент площади в интеграле
<
 2020-04-12
2020-04-12 2845
2845
