2020-04-12
145
Тема: «Решение обыкновенных дифференциальных уравнений».
Цель: научиться решать обыкновенные дифференциальные уравнения численными методами с заданной точностью различными методами для случаев, когда точное решение затруднено сложностью функции или невозможностью применения точных формул для случая табличного задания функции.
В результате выполнения лабораторной работы студент должен
ЗНАТЬ:
- постановку задачи Коши для дифференциального уравнения первого порядка;
- формулировку теоремы Пикара (без доказательства) о существовании и единственности решения задачи Коши;
- классификацию методов решения задачи Коши (аналитические – метод Пикара; графические; численные – метод Эйлера – Коши и его модификации, метод Рунге - Кутта);
УМЕТЬ:
- решать дифференциальное уравнение 1-го порядка аналитическими, графическими и численными методами (метод Пикара, метод Эйлера – Коши, метод Рунге - Кутта);
- реализовать численные методы решения задачи Коши на ЭВМ с заданной точностью;
|
|
|
- проводить сравнительный анализ точности решения с помощью «двойного» счета;
ИМЕТЬ ПРЕДСТАВЛЕНИЕ:
- об основных понятиях математического анализа (производная, окрестность точки, интеграл и т.д.);
- о графической интерпретации указанных методов.
Постановка задачи
Простейшим обыкновенным дифференциальным уравнением является уравнение 1-го порядка:
y’ = f(x, y) (1)
Основная задача, связанная с этим уравнением, известна как задача Коши:
Найти решение уравнения (1) в виде функции y(x), удовлетворяющей начальному условию:
f(x0)=y0. (2)
Существование и единственность решения уравнения обеспечивается следующей теоремой.
Теорема Пикара. Если функция f(x) определена и непрерывна в некоторой области G, определяемой параметрами: | x-x0 | £ a; | y-y0 | £ b (3)
и удовлетворяющей в этой области условию: | f(x,y1) – f(x,y2) | ≤ M · | y1 – y2 |, то на некотором отрезке | x – x0 | ≤ h, где h > 0 существует, и притом, только одно решение y=y(x) уравнения (1), удовлетворяющее начальному условию y0=y(x0). (Здесь M=const и M=max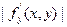 
)
Для решения дифференциальных уравнений методы решения подразделяются на 3 группы:
- аналитические методы, применение которых дает решение дифференциального уравнения в виде аналитического выражения;
- графические методы, дающие приближенное решение в виде графика;
- численные методы, когда искомая функция получается в виде таблицы.
|
|
|
Рассмотрим численное решение задачи Коши.
Метод Пикара
Этот метод позволяет получить приближенное решение дифференциального уравнения (1) в виде функции, представленной аналитически.
Пусть дано дифференциальное уравнение 1-го порядка y’ = f(x, y) с начальным условием f(x0)=y0. Проинтегрируем обе части уравнения от x0 до x:
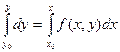или 
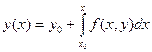(4)
Решение интегрального уравнения (4) будет удовлетворять дифференциальному уравнению (1) и начальному условию (2). Действительно, при x=x0 получим: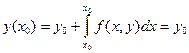 
. Кроме того, интегральное уравнение (4) позволяет применить метод последовательных приближений. Пусть 
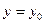. Получим первое приближение: 
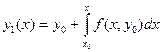. Интеграл в правой части содержит только переменную х; после нахождения этого интеграла будет получено аналитическое выражение приближения 
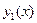. Заменим теперь в уравнении (4) y найденным значением 
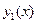и получим второе приближение: 
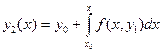и т.д. В общем случае итерационная формула имеет вид:
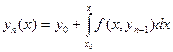(5)
Циклическое применение формулы (5) дает последовательность функций
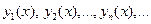. (6)
Ее предел является решением интегрального уравнения (5), а, следовательно, и дифференциального уравнения (1) с начальным условием (2). Это означает, что k – й член последовательности (6) является приближением к точному решению уравнения (1) с определенной степенью точности. Оценка погрешности k – го приближения дается формулой:
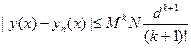(7)
где М = константа Лифшица, вычисляемая по формуле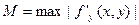 
, N – верхняя грань модуля функции f, определяемая по формуле 
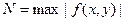, а величина d вычисляется по формуле 
.
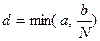Пример. Методом последовательных приближений найти приближенное решение дифференциального уравнения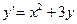 
, удовлетворяющее начальному условию 
.
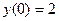Запишем для данного примера формулу вида (5):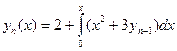 
. Начальным приближением будем считать 
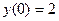. Имеем: 
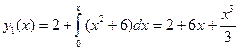. Далее получаем: 
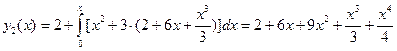. Аналогично получаем: 
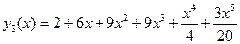и т.д.
Оценим погрешность 3-го приближения. Для определения области, заданной неравенствами (3), примем, например, a =1, b=2. В прямоугольнике G функция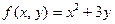 
определена и неприрывна, причем 
, 
, 
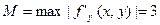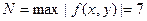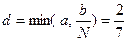. Используя оценочную формулу (7), получаем: 
.
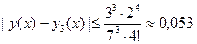Метод Эйлера
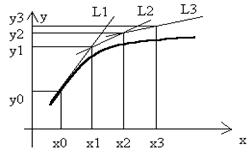В основе метода Эйлера лежит идея графического построения решения дифференциального уравнения, однако это метод дает одновременно и способ нахождения искомой функции в табличной форме.
Пусть дано уравнение (1) с начальным условием (2). Выбрав достаточно малый шаг h, построим, начиная с точки x0, систему равноотстоящих точек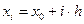 
(i = 0, 1, 2, …). Вместо искомой интегральной кривой на отрезке 
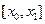рассмотрим отрезок касательной к ней в точке 
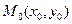(обозначим ее через L1) с уравнением 
.
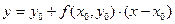При x=x1 из уравнения касательной L1 получаем: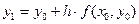 
, откуда видно, что приращение значения функции на первом шаге имеет вид: 
.
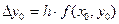Аналогично, проводя касательную L2 к некоторой интегральной кривой семейства в точке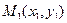 
, получим: 
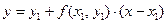, что при x=x2 дает 
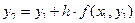, т.е. y2 получается из y1 добавлением приращения 
.
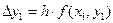Таким образом, получение таблицы значений искомой функции y(x) по методу Эйлера заключается в циклическом применении пары формул:
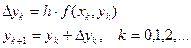(8)
Метод Эйлера обладает малой точностью, к тому же погрешность каждого нового шага систематически возрастает. Наиболее приемлемым для практики методом оценки точности является в данном случае способ дойного счета – с шагом h и с шагом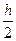 
. Совпадение десятичных знаков в полученных двумя способами результатах дат право считать их верными.
Пример. Решить методом Эйлера дифференциальное уравнение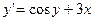 
с начальным условием 
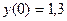на отрезке [0; 1], приняв шаг h = 0,2.
|
|
|
Результаты вычислений с двумя знаками после запятой приведены в таблицах 1 и 2.
Таблица 1. Таблица 2.
| x | y2h | yh |
| 0 | 1,30 | 1,30 |
| 0,1 | 1,33 | |
| 0,2 | 1,35 | 1,38 |
| 0,3 | 1,46 | |
| 0,4 | 1,52 | 1,56 |
| 0,5 | 1,68 | |
| 0,6 | 1,77 | 1,82 |
| 0,7 | 1,98 | |
| 0,8 | 2,09 | 2,15 |
| 0,9 | 2,33 | |
| 1,0 | 2,47 | 2,53 |
| k | xk | yk |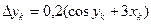 
|
| 0 | 0 | 1,30 | 0,05 |
| 1 | 0,2 | 1,35 | 0,16 |
| 2 | 0,4 | 1,52 | 0,25 |
| 3 | 0,6 | 1,77 | 0,32 |
| 4 | 0,8 | 2,09 | 0,38 |
| 5 | 1,0 | 2,47 |
Сопоставление приближений, полученных с различным шагом, показывает, что при выбранном шаге метод Эйлера дает невысокую точность – в пределах одной – двух значащих цифр.
Существуют различные уточнения метода Эйлера, повышающие его точность. Модификации метода обычно направлены на то, чтобы более точно определить направление перехода из точки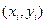 
в точку 
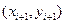. Примером такой модификации является метод Эйлера – Коши, рекомендующий следующий порядок вычислений:
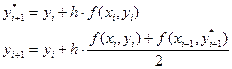(9)
Геометрически это означает, что определяется направление интегральной кривой в исходной точке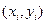 
и во вспомогательной точке 
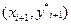, а в качестве окончательного берется среднее этих направлений.
Метод Рунге – Кутта
Метод Эйлера и метод Эйлера – Коши относятся к семейству методов Рунге – Кутта. В вычислительной практике наиболее часто используется метод Рунге – Кутта с q=4, s=4. Приведем без вывода один из вариантов соответствующих расчетных формул:
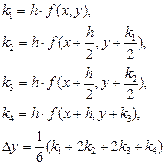(10)
В этом случае погрешность на шаге пропорциональна h5. Отсюда следует, что при достаточно малом h и малых погрешностях вычислений решение уравнения (1), полученное методом Рунге – Кутта, будет близким к точному.
Геометрический смысл использования метода Рунге – Кутта с расчетными формулами (10) состоит в следующем. Из точки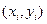 
сдвигаются в направлении, определяемом углом 
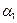, для которого 
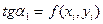. На этом направлении выбирается точка с координатами 
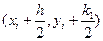. Затем из точки 
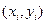сдвигаются в направлении, определяемом углом 
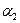, для которого 
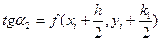, и на этом направлении выбирается точка с координатами 
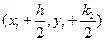. Наконец, из точки 
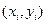сдвигаются в направлении, определяемом углом 
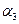, для которого 
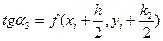, и на этом направлении выбирается точка с координатами 
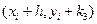. Этим задается еще одно направление, определяемое углом 
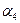, для которого 
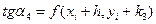. Четыре полученные направления усредняются в соответствии с последней из формул (10). На этом окончательном направлении и выбирается очередная точка 
.
|
|
|
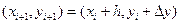Пример. Решить уравнение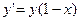 
с начальным условием 
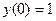методом Эйлера – Коши и методом Рунге – Кутта. Данное уравнение может быть решено аналитически. При заданных условиях оно выглядит так: 
.
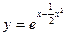Для сравнения сведем в таблицу 4 результаты численного решения уравнения указанными методами и значения точного решения.
Здесь:
1 – результаты, полученные методом Эйлера – Коши;
2 - результаты, полученные методом Рунге - Кутта;
3 – точное решение.
Таблица 4.
| x | 0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | |
| y | 1 2 3 | 1,000 1,000 1,0000 | 1,1050 1,0997 1,0997 | 1,2089 1,1972 1,1972 | 1,3095 1,2905 1,2095 | 1,4044 1,3771 1,3771 | 1,4912 1,4550 1,4550 | 1,5676 1,5220 1,5220 | 1,6316 1,5762 1,5762 | 1,6812 1,6405 1,6405 | 1,7152 1,6405 1,6405 |
Из примера видно, что метод Рунге – Кутта дает результаты, практически совпадающие с точным решением.
Задание
Решить задачу Коши для обыкновенного дифференциального уравнения y’ = f(x, y) на отрезке [a, b] при заданном начальном условии y(a) = c и шаге интегрирования h:
1) методом Эйлера с шагом h и 2h;
2) методом Рунге – Кутта с шагом h и 2h;
Замечание. Если возможно решить дифференциальное уравнение аналитическим методом, то сравнить точность методов, вычислив и точное решение функции в узловых точках с шагом h и 2h.
Таблица 5.
| В-т | Уравнение | a | b | c | h |
| 1 |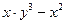 
| 4 | 5 | 0,7 | 0,1 |
| 2 |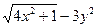 
| 2,6 | 4,6 | 1,8 | 0,2 |
| 3 |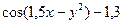 
| -1 | 1 | 0,2 | 0,2 |
| 4 |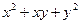 
| 2 | 3 | 1,2 | 0,1 |
| 5 |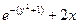 
| 0 | 0,5 | 0,3 | 0,05 |
| 6 |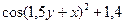 
| 1 | 2 | 0,9 | 0,1 |
| 7 |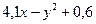 
| 0,6 | 2,6 | 3,4 | 0,2 |
| 8 |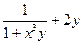 
| 1,5 | 2 | 2,1 | 0,05 |
| 9 |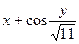 
| 2,1 | 3,1 | 2,5 | 0,1 |
| 10 |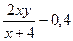 
| 3 | 5 | 1,7 | 0,2 |
| 11 |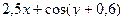 
| 1 | 3 | 1,5 | 0,2 |
| 12 |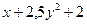 
| 1 | 2 | 0,9 | 0,1 |
| 13 |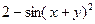 
| 2 | 3 | 2,3 | 0,1 |
| 14 |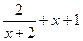 
| 0,1 | 0,5 | 1,25 | 0,05 |
| 15 |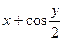 
| -2 | -1 | 3 | 0,1 |
