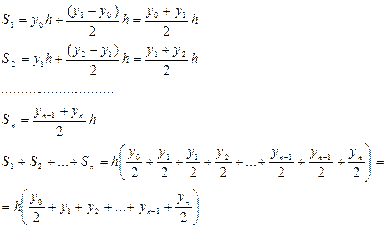Квадратурные формулы Ньютона – Котеса

Применение формулы (10) предполагает построение на отрезке [a, b] системы узлов интерполяции x₀, x₁, …, x_n. Длина x_i+1 – x_i = h – называется шагом интерполирования. Так как  - const, то в этом случае можно применить интерполяционную формулу Лагранжа для равноотстоящих узлов. Переходя к t, получим:

Числа                   (15)

называют коэффициентами Котеса.

Коэффициенты Котеса не зависят от функции f(x), а только от числа n точек разбиения.

Итак,                                                                   (16)

Формула трапеций

При n = 1 из формулы (15) имеем при i = 0;1: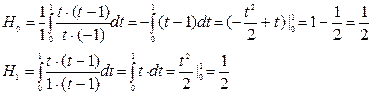

Тогда по формуле (16) на отрезке [x₀,x₁] получаем интеграл:

                                                (17)

Данная формула дает один из простейших способов вычисления определенного интеграла и называется формулой трапеций. Действительно, при n=1 подынтегральная функция заменяется интерполяционным полиномом Лагранжа 1-й степени (т.е. линейной функцией), а геометрически это означает, что площадь криволинейной фигуры подменяется площадью трапеции.

f(x)

                                                   

			Распространяя формулу (17) на все отрезки разбиения, получим общую формулу трапеций для отрезка [a, b]:                   (18)

 

 Действительно,

 

 

Пример. Вычислить интеграл по формуле трапеций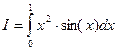

Разделим отрезок на 10 равных частей, т.е.  и построим таблицу значений в узловых точках x₀ = 0, x₁ = 0,1 и т.д. x₁₀ = 1.

x	0	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1
f(x)	0	0,001	0,008	0,027	0,062	0,120	0,203	0,316	0,499	0,634	0,842

Формула Симпсона

Рассмотрим коэффициенты Котеса (15) при n=2, т.е. при i = 0,1,2.

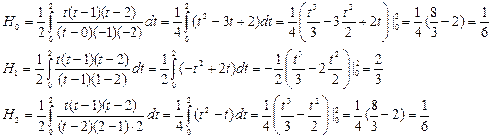
Тогда, с учетом (16) на отрезке [x₀, x₂] получаем интеграл:

Геометрически использование формулы (19) означает замену функции f(x) параболой L₂(x), проходящей через точки x₀, x₁, x₂. Если считать, что n – четное, то обобщая формулу (19), получим:

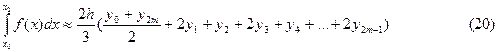
Формула (20) называется формулой Симпсона.

Формула Симпсона обладает повышенной точностью по сравнению с формулой трапеций, но только для полиномов до 3-й степени включительно.

Пример. Вычислить интеграл 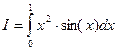по формуле Симпсона при том же числе отрезков разбиения n = 10.

x	0	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1
f(x)	0	0,001	0,008	0,027	0,062	0,120	0,203	0,316	0,499	0,634	0,842

Задание

1. Вычислить значение функции, заданной таблицей, в любой точке x по формуле Лагранжа для равноотстоящих узлов (табличные значения и число узловых точек задаются произвольно, n ≤ 10).

2. Вычислить значение производной функции, заданной таблично, используя интерполяционную формулу Лагранжа для равноотстоящих узлов (таблица 1). Провести проверку найденных значений по производной этой же функции, заданной аналитически.

3.  Вычислить значение производной функции, заданной таблично, используя интерполяционную формулу Ньютона в узловой точке x = x_i (табличные значения и число узловых точек задаются произвольно, n ≤ 10).

4. Вычислить значение интеграла (таблица 2) по формуле:

a) трапеций

b) Симпсона

Отрезок интегрирования разбивается на 10 равных частей. Значение в узловых точках вычислить по аналитическому представлению функции. Проверить точность вычислений по указанным формулам со значением интеграла, вычисленного аналитически (если это возможно).

Таблица 1.

№	таблица	a	b	H
1	1.1	0,65	0,75	0,01
2	1.2	0,30	0,45	0,025
3	1.3	1,45	1,55	0,01
4	1.4	1,20	1,40	0,02
5	1.2	0,10	0,20	0,01
6	1.3	1,10	1,30	0,02
7	1.4	1,05	1,25	0,025
8	1.1	0,70	0,90	0,02
9	1.3	1,25	1,50	0,025
10	1.4	1,00	1,10	0,01
11	1.1	0,60	0,70	0,01
12	1.2	0,15	0,35	0,025
13	1.4	1,15	1,25	0,01
14	1.1	0,65	0,85	0,025
15	1.2	0,20	0,40	0,02
16	1.3	1,15	1,25	0,01

 

 

 

Таблица 1.1.                     Таблица 1.2.                     Таблица 1.3.         Таблица 1.4.

X	sin x		x	cos x		x	sin x		x	cos x
0,60	0,56464		0,05	0,99875		1,10	0,89121		1,00	0,54090
0,65	0,60519		0,10	0,99500		1,15	0,91276		1,05	0,49757
0,70	0,64422		0,15	0,98877		1,20	0,93204		1,10	0,45360
0,75	0,68164		0,20	0,98007		1,25	0,94898		1,15	0,40849
0,80	0,71736		0,25	0,96891		1,30	0,96356		1,20	0,36236
0,85	0,75128		0,30	0,95534		1,35	0,97572		1,25	0,31532
0,90	0,78333		0,35	0,93937		1,40	0,98545		1,30	0,26750
0,95	0,81342		0,40	0,92106		1,45	0,99271		1,35	0,21901
1,00	0,84147		0,45	0,90045		1,50	0,99749		1,40	0,16997
1,05	0,86742		0,50	0,87758		1,55	0,99973		1,45	0,12050
1,10	0,89121		0,55	0,85252		1,60	0,99957		1,50	0,07074

Таблица 2.

№	f(x)	a	b
1	0,37·esinx	0	1
2	0,5x+x·lgx	1	2
3	(x+1,9)sin(x/3)	1	2
4		2	3
5		0	1
6	(2x+0,6)cos(x/2)	1	2
7	2,6x2lnx	1,2	2,2
8	(x2+1)sin(x-0,5)	0,5	1,5
9	x2cos(x/4)	2	3
10		3	4
11	3x+lnx	1	2
12		-1	0
13	3x2+tgx	-0,5	0,5
14		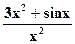0	1
15	3·x·ecosx	0,2	1,2
16		1,5	2,5