Нахождение приближающей функции в виде линейной функции и квадратного трехчлена (линейная и квадратичная регрессии)

Будем искать приближающую функцию в виде:

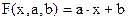                           (7)

Найдем частные производные по параметрам:

Составим теперь систему вида:

Сумма здесь и далее берется по параметру i в пределах от 1 до n. Далее имеем:

Или, деля каждое уравнение на n:

Введем обозначения:

Тогда последняя система будет иметь вид:

Коэффициенты этой системы M_x, M_x2, M_xy, M_y – числа, которые в каждой конкретной задаче приближения могут быть легко вычислены по формулам, а x_i, y_i -значения из таблицы.

Решив систему, получим значения параметров a и b, а следовательно, и конкретный вид линейной функции.

В случае нахождения приближающей функции в виде квадратичной, имеем:

Находим частные производные: . Составим систему вида:

После несложных преобразований получается система трех уравнений с неизвестными a, b, c. Коэффициенты системы, так же как и в случае линейной функции, выражаются только через известные данные из таблицы:

Здесь

Решение системы дает значения параметров a, b, c для приближающей функции.

 

Нахождение приближающей функции в виде других элементарных функций

 

Степенная функция (геометрическая регрессия)

Будем искать приближающую функцию в виде: . Предполагая, что в исходной таблице значения функции положительны, прологарифмируем равенство при условии a>0:

Ln F = ln a + m ln x.

Введем новую переменную u = ln x. Тогда ln F будет функцией от u: Ф(u). Обозначим:

m = A, ln a = B.

Теперь равенство принимает вид: Ф(u, A, B) = A·u + B, т.е. задача свелсь к отысканию приближающей функции в виде линейной.