Показательная функция

Пусть исходная таблица такова, что приближающую функцию целесообразно искать в виде показательной функции: 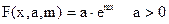. Прологарифмируем равенство:

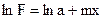
Приняв обозначения m = A, ln a = B, перепишем равенство в виде:

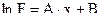
Таким образом, для нахождения приближающей функции в виде показательной, нужно прологарифмировать значения функции в исходной таблице, и, рассматривая их совместно с исходными значениями аргумента, построить для новой таблицы приближающую функцию вида 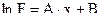. Далее в соответствии с обозначениями m = A, ln a = B, остается получить значения искомых параметров a и b и подставить их в формулу.

Дробно – линейная функция

Будем искать приближающую функцию в виде: 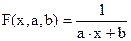. Равенство перепишем в виде: 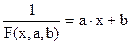. Из последнего равенства следует, что для нахождения значений параметров a и b по заданной таблице, нужно составить новую таблицу, у которой значения аргумента оставить прежними, а значения функции заменить обратными числами, после чего для полученной таблицы получить приближающую функцию вида ax+b. Найденные значения параметров a и b подставить в формулу.

Логарифмическая функция

Пусть приближающая функция имеет вид: 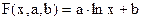. Легко видеть, что для перехода к линейной функции достаточно сделать подстановку ln x = u. Отсюда следует, что для нахождения значений a и b нужно прологарифмировать значения аргумента в исходной таблице, и,рассматривая полученные значения в совокупности с исходными значениями функции, найти для полученной таким образом новой таблицы приближающую функцию в виде линейной.

Гипербола

Если точечный график, построенный по таблице, дает ветвь гиперболы, приближающую функцию можно искать в виде: 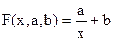. ДЛЯ перехода к линейной функции сделаем подстановку 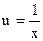. Практически перед нахождением приближающей функции следует значения аргумента в исходной таблице заменить обратными числами и найти для новой таблицы приближающую функцию в виде линейной.