Энергия заряженного проводника и конденсатора

Сообщение заряда проводнику связано с совершением работы по преодолению сил кулоновского отталкивания. Эта работа идет на увеличение электрической энергии проводника. Элементарная работа  по перенесению малого заряда  из бесконечности на уединенный проводник равна , т.к. . Здесь  – потенциал проводника, а  – его емкость. Работа по сообщению проводнику потенциала  равна . С учетом того, что , энергия проводника может быть выражена как

.                                     (5.11)

Аналогичные выражения получаются и для конденсатора

.                                        (5.12)

Для конденсатора последнее выражение представим в виде

,

тогда для произвольной системы проводников , где  – потенциал 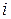-го проводника в поле, созданном остальными проводниками.

Энергия электрического поля

Получим выражение для энергии электрического поля на примере плоского конденсатора. Для плоского конденсатора справедливы выражения , следовательно,

,

где  – объем, в котором сосредоточено электрическое поле конденсатора;

 –                                        (5.13)

объемная плотность энергии электрического поля.

Преобразуем выражение для объемной плотности энергии электрического поля. С учетом того, что , объемная плотность энергии электрического поля

.                               (5.14)

Первое слагаемое данного выражения есть плотность энергии поля, созданного свободными зарядами, второе слагаемое – плотность энергии поляризованного диэлектрика.

Литература

1. Детлаф А. А. Курс физики / А. А., Б. М. Яворский. – М.: Высшая школа, 2000.

2. Волькенштейн В. С. Сборник задач по общему курсу физики / В. С. Волькенштейн. - М.: Наука, 2002.

3. Чертов А. Г. Задачник по физике / А. Г. Чертов, А. А. Воробьев. - М.: Высшая школа, 1988.