Внаслідок елементарних перетворень система рівнянь переходить у рівносильну систему рівнянь (з урахуванням зміни нумерації невідомих)

Метод Гаусса полягає в послідовному виключенні невідомих за допомогою елементарних перетворень системи.

Розглянемо перше рівняння системи. Нехай а ₁₁ 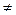0. Поділимо обидві частини першого рівняння на а₁₁. До другого рівняння додамо перше, помножене на (- а ₂₁), одержимо друге рівняння, в якому виключено невідоме х ₁. Аналогічно за допомогою першого рівняння з кожного наступного виключимо невідоме х ₁.

Розглянемо друге рівняння. Якщо в ньому усі коефіцієнти при невідомих і вільний член дорівнюють нулю, то переставляємо це рівняння на останнє місце. Якщо усі коефіцієнти при невідомих дорівнюють нулю, а вільний член не дорівнює нулю, то система розв’язків не має. Нехай у другому рівнянні коефіцієнт при х ₂ не дорівнює нулю 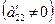. Поділимо обидві частини другого рівняння на 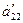, До третього і кожного наступного додамо друге рівняння, помножене на коефіцієнт при х ₂ у кожному з цих рівнянь. В результаті всі рівняння, починаючи з третього не будуть містити невідоме х ₂. Продовжуючи такі дії з кожним із рівнянь у випадку квадратної системи (число рівнянь дорівнює числу невідомих) одержимо систему в такому вигляді:

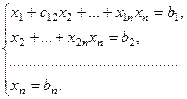
З цієї системи можна знайти всі невідомі х _i, тобто - розв’язок системи.

Розв’язуючи систему методом Гаусса, зручно записувати тільки розширену матрицю системи і виконувати елементарні перетворення, що приведуть матрицю до трапецієподібного вигляду.

Означення 16

Розширеною матрицею системи називають матрицю, в якій до основної матриці системи приєднали стовпець вільних членів, тобто

=

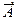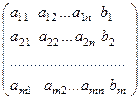
Приклад 10

Розв’язати методом Гаусса систему рівнянь:

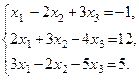
1. Запишемо розширену матрицю, виконаємо елементарні перетворення за алгоритмом Гаусса:

=

.

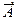
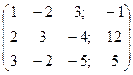
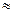
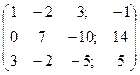
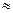
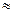
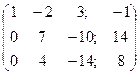
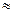
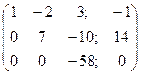
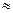
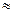
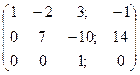2. Таким чином, одержали систему, рівносильну даній:

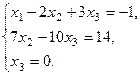
3. З цієї системи знаходимо розв’язок системи: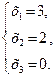

Відповідь.(3, 2, 0)