Розглядається n галузей промисловості, кожна з яких виробляє свою продукцію, частина якої використовується для внутрішніх потреб, а частина для суспільних потреб (поза матеріальним виробництвом). Процес виробництва розглядається протягом деякого часу (наприклад, року).
Позначимо:
хi – валовий об’єм продукції i-ої галузі  ;
;
хij – об’єм продукції i - ої галузі, що використовується в j -ій галузі в процесі виробництва  ;
;
yi – об’єм кінцевого продукту i -ої галузі для невиробничого споживання;
Співвідношення балансу – це рівняння 
Коефіцієнти прямих затрат а ij =  показують затрати продукції i -ої галузі на виробництво одиниці продукції j -ої галузі. Вважають, що коефіцієнти – сталі числа на деякому проміжку часу. Це означає лінійну залежність матеріальних затрат від валового випуску, тобто,
показують затрати продукції i -ої галузі на виробництво одиниці продукції j -ої галузі. Вважають, що коефіцієнти – сталі числа на деякому проміжку часу. Це означає лінійну залежність матеріальних затрат від валового випуску, тобто,  . Співвідношення балансу мають такий вигляд:
. Співвідношення балансу мають такий вигляд:

Це рівняння можна записати в матричному вигляді:
Х= АХ + Y (*), де А =  , Х=
, Х=  , Y =
, Y = 
Основна задача міжгалузевого балансу полягає в тому, щоб знайти вектор валового виробництва Х, який при відомій матриці прямих затрат А забезпечує заданий вектор кінцевого продукту Y.
Рівняння (*) можна розв’язати: Х = (Е–А)-1 Y, матриця S = (E–
– A)-1 називається матрицею повних затрат. Матриця А  називається продуктивною, якщо для будь-якого вектора Y
називається продуктивною, якщо для будь-якого вектора Y  існує розв’язок Х
існує розв’язок Х  рівняння (*). У цьому випадку модель Леонтьєва називається продуктивною.
рівняння (*). У цьому випадку модель Леонтьєва називається продуктивною.
III. Завдання для самостійної роботи.
1. Обчислити визначники.
1).  =
=  (В.
(В.  = 22)
= 22)
2)  =
=  (В.
(В. 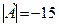 ).
).
3)  =
=  (В.
(В.  =68)
=68)
4)  =
=  (В.
(В.  ).
).
2. Задані матриці
А=  Знайти АС; АВ.
Знайти АС; АВ.
3. З’ясувати, чи існує матриця, обернена матриці А.
А = 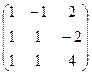 , і якщо існує, знайти її. Виконати перевірку: АА-1 = Е.
, і якщо існує, знайти її. Виконати перевірку: АА-1 = Е.
4. Обчислити АВ – ВА, якщо:
А=  , В=
, В=  .
.
5. Розв’язати задану систему трьома методами:
1) матричним;
2) за формулами Крамера;
3) методом Гаусса-Жордана:
а) 
б) 
в) 
6. Дослідити системи на сумісність та знайти загальний розв’язок. Використати метод Гаусса.
а) 
б) 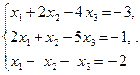
в) 
г) 
д) 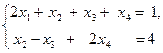
IV. Завдання для контрольної роботи.
Завдання 1
Дано дві матриці А і В. Знайти:
а) добуток матриць А∙В;
б) обернену матрицю  ;
;
в) знайти  ;
;
1. 
2. 
3. 
4.  .
.
5.  .
.
6.  .
.
7.  .
.
8.  .
.
9. 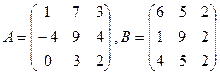 .
.
10.  .
.
11.  .
.
12.  .
.
13.  .
.
14.  .
.
15.  .
.
16. 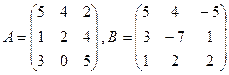 .
.
17.  .
.
18. 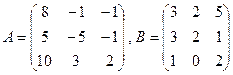 .
.
19.  .
.
20.  .
.
21. 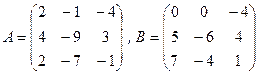 .
.
22.  .
.
23.  .
.
24. 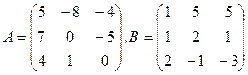 .
.
25.  .
.
26.  .
.
27.  .
.
28.  .
.
29.  .
.
30.  .
.
Завдання 2
Розв’язати систему рівнянь:
а) за формулами Крамера;
б) матричним методом;
в) методом Гаусса-Жордана.
 | |||
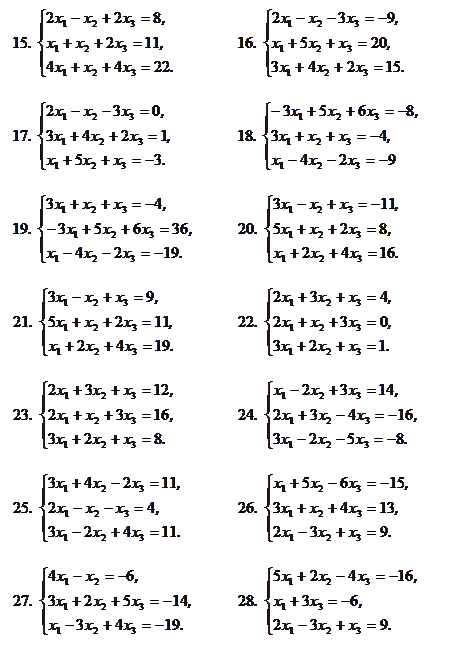 | |||
V. Список використаної і рекомендованої літератури.
- Апатенок Р.Ф.Элементы линейной алгебры. – Мн. «Вышейш. школа», 1977.
- Гетманцев В. Д. Лінійна алгебра і лінійне програмування: навчальний посібник. – К.: Либідь, 2002. – 256 с.
- Данко П.Б., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. - М.Высш.шк.,1980-1984,т.1.
- Дискант В.І. Береза Л. Р. і інші. Збірник задач з лінійної алгебри та аналітичної геометрії. – К.: Вища шк., 2001.- 303 с.
- Кремер Н.Ш. Путко И.М. и др. Высшая математика для экономистов: Учебник для вузов. – М.: Банки и биржи, ЮНИТИ, 1999. – 471 с.
- Тевяшев А. Д., Литвин О.Г. Вища математика у прикладах і задачах. ч. 1. Лінійна алгебра і аналітична геометрія. Диференціальне числення функцій однієї змінної. – Харків: ХТУРЕ.2002 – 552 с.
- Шнейдер В.Е., Слуцкий А.И., Шумов А.С. Краткий курс высшей математики. – М.: Высш.шк.,1978, т.1.
- Барковський В.В., Барковська Н.В. Вища математика для економістів. – Київ: ЦУЛ, 2002. – 400 с. – Серія: математичні науки.
Здано до набору 12.08.03. Підписано до друку 30.08.03.
Формат 145×210. Папір 80г/м2, обкладинка 80г/м2.
Друк лазерний.
Віддруковано на обладнанні

 2020-04-12
2020-04-12 86
86







