Признак сходимости для несобственных интегралов 1-ого рода

Пусть функции f (x) и g (x) интегрируемые по любому отрезку [ a; b ] и при x ≥ a удовлетворяют неравенствам  . 

Тогда: 

(эти утверждения имеют простой смысл: если сходится интеграл от большей функции, то сходится интеграл и от меньшей функции; если расходится интеграл от меньшей функции, то расходится интеграл и от большей функции; в случаях, когда сходится интеграл от меньшей функции или расходится интеграл от большей функции, никаких выводов о сходимости второго интеграла сделать нельзя). 

В качестве “стандартного” интеграла, с которым сравнивается данный, 

Дирихле. Этот интеграл сходится, если p > 1, и расходится, если p ≤ 1:   

 

 

Следствие из признака сходимости:

В качестве функции  берётся подынтегральная функция, так называемого “ стандартного ” интеграла, т. е. 

Если задание формулируется таким образом: “ исследовать несобственный интеграл на сходимость ”, то при решении задачи следует воспользоваться следствием из признака сходимости.

Пример: исследовать интеграл на сходимость.

В качестве “стандартной” рассмотрим функцию   , тогда      

расходится, как и интеграл от “стандартной” функции при степени

 

Пример: исследовать интеграл на сходимость.

 

В качестве “стандартной” рассмотрим функцию    

(соответствующую старшей степени слагаемого в знаменателе)

 

по третьему  замечательному пределу. Следовательно, исследуемый интеграл сходится, степень p = 2 > 1.   

Пример: исследовать интеграл на сходимость.

 

В качестве “стандартной” рассмотрим функцию  , тогда

 

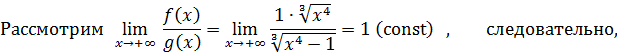
исследуемый интеграл при x→+∞ ведет себя так же, как и стандартный, т. е. сходится. 

 

1.3. Несобственные интегралы от неограниченных на отрезке [ a, b ] функций.

Несобственные интегралы от неограниченных на отрезке [ a,b ] функций называются несобственными интегралами 2 – ого рода. 

Пусть функция f(x) непрерывна на [ a; b) и не ограничена вблизи “ b ”.

Если f(x) непрерывна на (a; b ], но не ограничена вблизи “ a ”, тогда 

Если функция непрерывна на (a,b) но не ограничена вблизи и точек а и b, то несобственный интеграл 2-ого рода определяется равенством:

Если функция f(x) непрерывна на отрезке [ a; b ] всюду, кроме некоторой точки “ с ”, где a < c < b  и не ограничена вблизи “ c ”, то

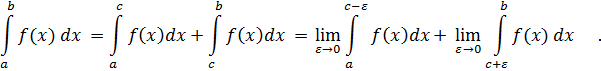
Пример: вычислить несобственный интеграл или установить его расходимость.

Точка x = 0 – точка разрыва подынтегральной функции.  

 

 

Пример: вычислить несобственный интеграл или установить его расходимость.

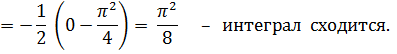
(Точка x = 1 – точка разрыва подынтегральной функции ε > 0; ε → 0).

 

Пример: вычислить интеграл или установить его расходимость.

 

 

Пример: вычислить интеграл или установить его расходимость.

 

 

Точками разрыва подынтегральной функции являются и верхний и нижний пределы интегрирования. Решаем интеграл методом разбиения подынтегральной функции на элементарные дроби 1 – ого рода.

 

 

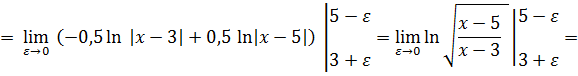
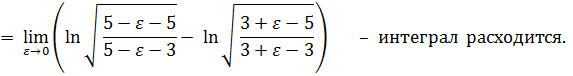
Разность логарифмов равна логарифму частного, т.е. I=1/2 lim ln(ε²/(2-ε)²)=∞.