Признак сравнения для несобственных интегралов 2 – ого рода

Пусть функции f(x) и g (x)  интегрируемы по любому отрезку              [ a+ ε; b ]   (0 < ε < b - a) и при x > a удовлетворяют неравенствам              .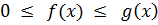  

Тогда: 

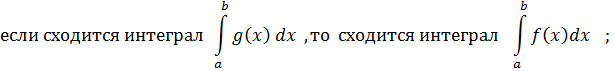
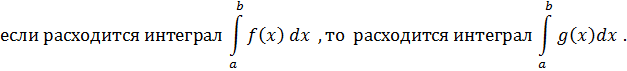
В качестве “стандартного” интеграла, с которым сравнивается данный, и в этом случае обычно берётся интеграл от степенной функции типа

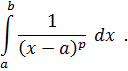
Этот интеграл сходится, если  p < 1, и расходится, если  p ≥ 1:

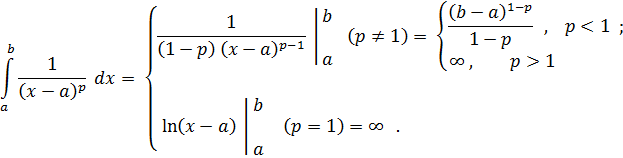
Если функция f(x) неограниченно возрастает при x→ b, то в качестве “стандартного” рассматривается интеграл

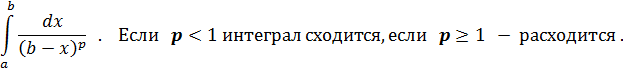
Пример: исследовать на интеграл на сходимость.

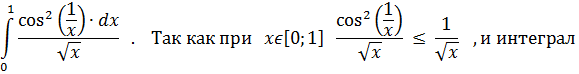
от большей функции сходится, то данный интеграл сходится; p =   <1.

Пример: исследовать интеграл на сходимость.

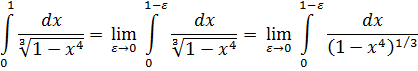
Так как p =   <1, то интеграл сходится.

Пример: исследовать интеграл на сходимость.

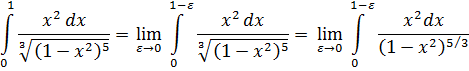
Так как p = 1, то, следовательно, интеграл расходится.