2020-04-07
174
Любую прямоугольную таблицу можно суммировать сначала по строкам, и затем сложить все полученные результаты, а можно сначала по столбцам. Но в итоге всё равно получится сумма всех элементов. Подобное есть и для двойных интегралов. Можно разбить поверхность на сечения вдоль оси 
, а можно в перпендикулярном направлении, вдоль 
. Для прямоугольной области:
= 
.
Но проблема возникает в том случае, когда область не прямоугольная. Там так просто заменить интегралы наоборот уже не получится, ведь границы внутреннего зависят от внешней переменной. В этом случае надо заново рассмотреть (с помощью чертежа) поведение одной переменной в зависимости от другой. Можно провести не вертикальные, а горизонтальные отрезки, и найти их пересечения с областью определения. Теперь нужны не верхняя и нижняя граница, а левая и правая.
Пример. Вычислить 
, по треугольнику с вершинами (0,0), (1,0), (1,1), (как в прошлом примере), сменив порядок интегрирования таким образом, чтобы внешний интеграл был по 
.
Решение. Спроецируем всю фигуру на ось . Проекция есть отрезок 
. Итак, 
. Теперь надо узнать, от чего до чего меняется 
при каждой отдельно взятой высоте . Отметим зелёным цветом горизонтальные линии. Чем выше, тем позже начинается движение точки внутри треугольника. Можно выразить это с помощью обратной функции 
. Завершается на любой высоте при абсциссе 1. Таким образом,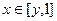 
. Тогда интеграл, записанный в прошлом примере как 
, примет вид 
= 
= 
= 
= 
= 
.
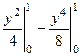Пример. Сменить порядок интегрирования 
.
Сначала построим чертёж. Закрасим область под параболой. Это область определения D функции двух переменных.
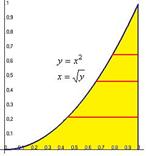
Глобальные границы по от 0 до 1, так как ниже 0 или выше 1 вообще нет точек этой фигуры Теперь надо узнать, от какой до какой абсциссы будет проходить горизонтальный отрезок внутри фигуры. Нужно границу 
записать с помощью обратной функции: 
. Горизонтальная линия чем выше, тем позже начинается, а именно от линии 
, а заканчивается всё время при 
.
Итак, = 
.
