Кроме пары чисел 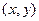 , которыми можно задать точку на плоскости, можно задать также и таким образом: соединим точку с началом координат, длину этого отрезка обозначим
, которыми можно задать точку на плоскости, можно задать также и таким образом: соединим точку с началом координат, длину этого отрезка обозначим  . Угол между осью
. Угол между осью  и этим отрезком обозначим
и этим отрезком обозначим  .
.

Так как  это прилежащий катет, а
это прилежащий катет, а 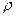 гипотенуза, тогда
гипотенуза, тогда  , аналогично
, аналогично  , откуда следуют такие формулы:
, откуда следуют такие формулы:

Также возможен обратный пересчёт:  , а угол:
, а угол:  (это верно для 4 и 1 четвертей, то есть там, где основная непрерывная ветвь тангенса) и
(это верно для 4 и 1 четвертей, то есть там, где основная непрерывная ветвь тангенса) и  для 2,3 четвертей.
для 2,3 четвертей.
Диапазоны изменения таковы:  ,
,  .
.
При замене переменных, соответственно, надо все переменные  , присутствующие в функции, заменить на
, присутствующие в функции, заменить на  , а все
, а все  на
на  , то есть получим
, то есть получим  . Однако необходимо ещё заменить дифференциал, если помните, в 1-мерном случае это делали так: например, при
. Однако необходимо ещё заменить дифференциал, если помните, в 1-мерном случае это делали так: например, при  было
было  . В двумерном случае, дополнительный множитель также есть. Если бы просто написали
. В двумерном случае, дополнительный множитель также есть. Если бы просто написали  вместо
вместо  , то неверно задали бы искажение сетки координат при замене. Если изобразить дуги и радиусы, то сектора круга сужаются к центру, а когда переносим изображение в плоскость параметров
, то неверно задали бы искажение сетки координат при замене. Если изобразить дуги и радиусы, то сектора круга сужаются к центру, а когда переносим изображение в плоскость параметров  то мы растягиваем эту сетку на некоторый прямоугольник, зелёный сектор по площади гораздо меньше красного, но без правильного пересчёта дифференциалов они получились бы равны. Чертёж - слева в плоскости параметров
то мы растягиваем эту сетку на некоторый прямоугольник, зелёный сектор по площади гораздо меньше красного, но без правильного пересчёта дифференциалов они получились бы равны. Чертёж - слева в плоскости параметров 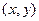 , справа в плоскости
, справа в плоскости  .
.

При том же растворе угла, чем ближе сектор к центру, тем меньше его площадь, и соответственно, меньше его влияние на интеграл. Для правильного учёта этих искажений, надо умножить на определитель матрицы линейного оператора порядка 2, эта матрица в то же время и является производной матрицей отображения 

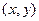 .
.
При замене двух старых на две новые переменные в плоскости, существует уже 4 различных частных производных, и из них можно образовать матрицу 2-го порядка. Строение этой матрицы:  .
.
Она называется матрицей Якоби, а её определитель - определителем Якоби, или «якобианом». В данном случае,
 =
=  , определитель:
, определитель:  =
= 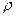 .
.
Итак, доказали, что определитель Якоби полярной системы координат:  . Выражение
. Выражение  заменяется на
заменяется на  .
.
Интеграл по той части фигуры, которая ближе к центру, как раз и будет взят с меньшим весом, а которая дальше от центра - с большим весом, ведь там 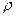 больше. При замене
больше. При замене  , где
, где  , множитель
, множитель  фактически является одномерным якобианом, но только для матрицы порядка 1 определитель вычислять было не нужно, так как он совпадает с самим этим элементом.
фактически является одномерным якобианом, но только для матрицы порядка 1 определитель вычислять было не нужно, так как он совпадает с самим этим элементом.
При переходе к полярным координатам, фрагмент круга фактически отображается в прямоугольную область. А это удобнее для вычисления, так как границы внутреннего и внешнего циклов становятся независимы друг от друга.
Замечание. В декартовых координатах такие интегралы имели бы вид:
 , что при вычислении внутреннего интеграла привело бы к выражениям с корнем типа
, что при вычислении внутреннего интеграла привело бы к выражениям с корнем типа  и потребовало бы в некоторых примерах серию из нескольких подстановок.
и потребовало бы в некоторых примерах серию из нескольких подстановок.
ЛЕКЦИЯ № 3. 12.02.2020
Рассмотрим несколько примеров на тему «полярные координаты».
Пример. Доказать формулу площади круга  с помощью полярных координат.
с помощью полярных координат.
Решение. Так как надо вычислить площадь, то считаем  .
.
 =
=  =
=  =
=  =
=  =
=  .
.
Пример. Вычислить интеграл  где D - четверть круга единичного радиуса в первой четверти плоскости.
где D - четверть круга единичного радиуса в первой четверти плоскости.
В декартовых координатах, этот интеграл имеет такой вид:
 , что при вычислении внутреннего интеграла дало бы
, что при вычислении внутреннего интеграла дало бы  , в итоге привело бы к
, в итоге привело бы к  и потребовало бы ещё серию подстановок. В полярных координатах, решение гораздо более просто и удобно.
и потребовало бы ещё серию подстановок. В полярных координатах, решение гораздо более просто и удобно.
Луч находится в 1 четверти при  . Радиус 1. Тогда:
. Радиус 1. Тогда:
 =
=  =
=  =
=  =
=
=  =
=  =
=
 =
=  =
=  =
=  .
.
Кстати, множители, не зависящие от 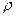 , можно было сразу вынести во внешний интеграл, как видим, они всё равно умножаются на первообразную по
, можно было сразу вынести во внешний интеграл, как видим, они всё равно умножаются на первообразную по 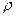 и остаются неизменными, и выносятся во внешний интеграл по
и остаются неизменными, и выносятся во внешний интеграл по  .
.
Пример. Вывести формулу площади сферы  .
.
Решение.
Вспомним формулу S поверхности  ,
,
рассмотрим верхнюю полусферу, она задана функцией:  .
.
При этом область определения данной функции - плоская область D - это круг радиуса  .
.
 ,
,  . Тогда
. Тогда
 =
= 
=  =
=
 =
=  . Теперь переходим к полярным координатам, заодно домножая на определитель Якоби
. Теперь переходим к полярным координатам, заодно домножая на определитель Якоби 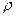 .
.
 =
= 
(домножили и поделили на 2, чтобы образовать полный дифференциал подкоренного выражения  ).
).
 =
=  =
=  =
=
 =
=  =
=  . Напомним, что это площадь верхней полусферы. Соответственно, площадь всей сферы в 2 раза больше, и равна
. Напомним, что это площадь верхней полусферы. Соответственно, площадь всей сферы в 2 раза больше, и равна  .
.
 2020-04-07
2020-04-07 160
160








