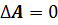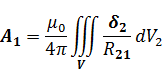Векторный магнитный потенциал
Уровнения векторного потенциала.
В соответствии с основной теоремой векторного анализа, соленоидальное магнитное поле (d 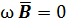 ) обладает векторным магнитным потенциалом А, который вводится условием
) обладает векторным магнитным потенциалом А, который вводится условием 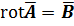 . При этом условие соленоидальности магнитного поля выполняется само собой
. При этом условие соленоидальности магнитного поля выполняется само собой
(d 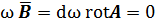 ). Что бы поле A определялось однозначно, необходимо задать его дивергенцию. Сделать это нужно так, что бы не нарушались уравнения электрического поля. Если магнитное поле создано постоянными токами и постоянными магнитами, неподвижными в пространстве, то можно положить:
). Что бы поле A определялось однозначно, необходимо задать его дивергенцию. Сделать это нужно так, что бы не нарушались уравнения электрического поля. Если магнитное поле создано постоянными токами и постоянными магнитами, неподвижными в пространстве, то можно положить:
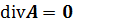
|
(Во всяком случае приемлемость этого простейшего ограничения на 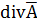 нужно проверить.)
нужно проверить.)
Теперь закон Ампера (полного тока) приводит к выводу, векторный магнитный потенциал подчиняется векторному уравнению Пуассона. Действительно, 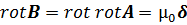 . Согласно известной формуле векторного анализа
. Согласно известной формуле векторного анализа
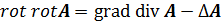 а из условия (12) следует, что
а из условия (12) следует, что
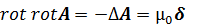 . .
|
Таким образом
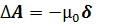 (13) (13)
|
Это уравнение является сокращённой записью трёх скалярных уравнений:
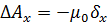
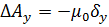
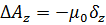
Снаружи проводников, по которым протекают магнитный потенциал удовлетворяет уравнению Лапласа
|
| ||
Фундаментальное решение уравнения (13) представляется виде объёмного векторного потенциала:
|
| |
Это сокращённая запись трёх скалярных объёмных потенциалов
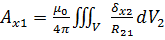
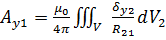
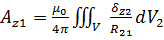
Интегрирование выполняется по объёму проводников с током. Точка нулевого потенциала находится на бесконечности.
Векторный потенциал плоскопараллельного магнитного поля.
Рассмотрим магнитное поле длинного прямолинейного провода с током i, который направлен вдоль оси OZ. Магнитная индукция легко определяется по закону Ампера (полного тока) 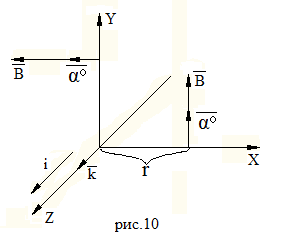
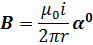
|
в цилиндрической системе координат. Так как 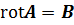 и имеет только азимутальную составляющую то
и имеет только азимутальную составляющую то
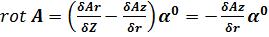 , ,
|
Следовательно, A имеет только аксиальную компоненту 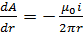 .
.
Таким образом, 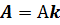 ,
,
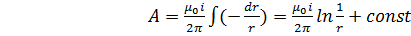 (14)
(14)
Значение логарифмического потенциала A зависит от точки выбора нулевого потенциала [тот же результат получается, если воспользоваться формулой (10):
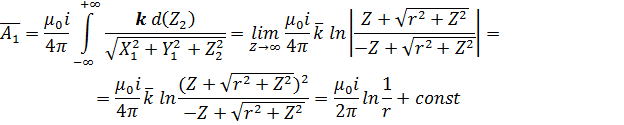
|
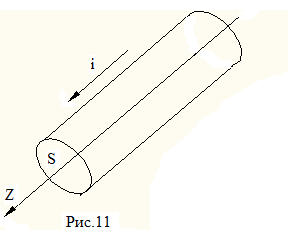
Магнитное поле длинного магнитного провода с поперечным сечением S можно рассчитать,
применив принцип наложения. Разобьём провод на нити, параллельные оси Oz и несущие ток 
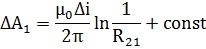
После перехода к пределу интегральная сумма превращается в интеграл по поперечному сечению провода
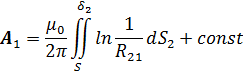
|
Здесь 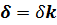
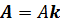
 2020-04-07
2020-04-07 159
159