Моделирование переходного процесса аналитическим методом в цепи R-L средствами ядра Matlab

Таблица 3.1. Параметры для расчёта

Напряжение питания цепи, В	Резистивное сопротивление катушки, Ом	Индуктивность катушки, Гн
27	150	0,14

При выполнении задания рекомендуется использовать аналитический метод решения дифференциальных уравнений (1.1) и (1.2) для тока и напряжения на индуктивном элементе в цепи с катушкой индуктивности, включаемой на постоянное напряжение.

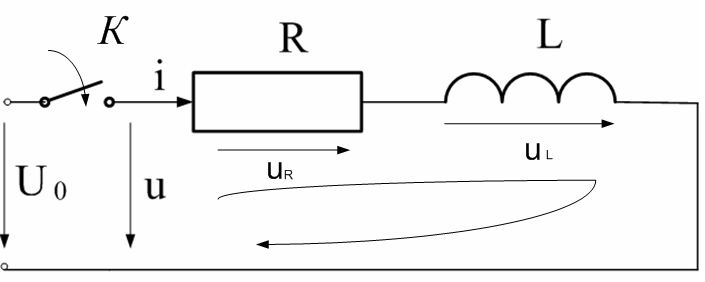
Рис.3.1. Электрическая цепь с последовательным соединением резистора и катушки индуктивности

При моделировании необходимо правильно выбрать величину шага квантования. Чем меньше выбрана величина шага квантования, тем меньше будет ошибка интегрирования.

Выбор величины шага квантования определяется теоремой Котельникова – Шеннона (формула (1.4)). Тогда шаг квантования с применением для расчета эмпирической формулы будет равен:

Рассчитаем и построим график тока в цепи с катушкой индуктивности при включении её на постоянное напряжение. Заносим все данные и формулы в Matlab в окне редактора «М-файлов».

Рис.3.2. Программа расчёта тока в цепи с катушкой индуктивности

Переносим данные в командное окно и нажимаем клавишу Enter. Matlab выдаёт нам график тока в цепи с катушкой индуктивности при включении её на постоянное напряжение.

Рис.3.3. График зависимости тока в цепи с катушкой индуктивности от времени

Рассчитаем и построим график напряжения на индуктивном элементе в цепи с катушкой индуктивности при включении её на постоянное напряжение. Заносим все данные и формулы в Matlab в окне редактора «М-файлов».

Рис.3.4. Программа расчёта напряжения на индуктивном элементе в цепи с катушкой индуктивности

Переносим данные в командное окно и нажимаем клавишу Enter. Matlab выдаёт нам график напряжения на индуктивном элементе в цепи с катушкой индуктивности при включении её на постоянное напряжение.