2020-04-12
145
Таблица 4.1. Параметры для расчёта
| Ёмкость конденсатора, мкФ | Сопротивление резистора, Ом | Напряжение питания цепи, В |
| 0,2 | 104 | 20 |
При выполнении задания рекомендуется использовать аналитический метод решения дифференциальных уравнений (2.1) и (2.2) для тока и напряжения на конденсаторе в цепи, включаемой на постоянное напряжение.
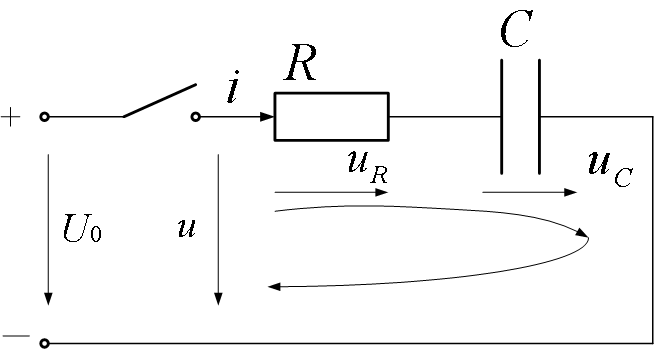
Рис.4.1. Электрическая цепь с последовательным соединением резистора и конденсатора
При моделировании необходимо правильно выбрать величину шага квантования. Чем меньше выбрана величина шага квантования, тем меньше будет ошибка интегрирования.
Выбор величины шага квантования определяется теоремой Котельникова – Шеннона (формула (1.4)). Тогда шаг квантования с применением для расчета эмпирической формулы будет равен:
Рассчитаем и построим график напряжения на конденсаторе в цепи при включении её на постоянное напряжение. Заносим все данные и формулы в Matlab в окне редактора «М-файлов».
|
|
|
Рис.4.2. Программа расчёта напряжения на конденсаторе в цепи
Переносим данные в командное окно и нажимаем клавишу Enter. Matlab выдаёт нам график напряжения на конденсаторе в цепи при включении её на постоянное напряжение.
Рис.4.3. График зависимости напряжения на конденсаторе в цепи от времени
Рассчитаем и построим график тока в цепи с конденсатором при включении её на постоянное напряжение. Заносим все данные и формулы в Matlab в окне редактора «М-файлов».
Рис.4.4. Программа расчёта тока в цепи с конденсатором
Переносим данные в командное окно и нажимаем клавишу Enter. Matlab выдаёт нам график тока в цепи с конденсатором при включении её на постоянное напряжение.
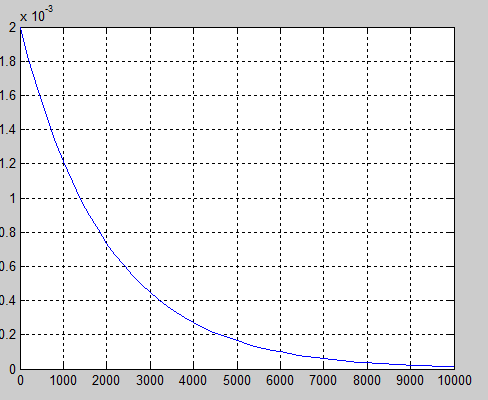
Рис.4.5. График зависимости тока в цепи с конденсатором от времени
Моделирование переходного процесса при подключении цепи R-L к источнику постоянного напряжения методом уравнений состояния средствами Excel
Таблица 5.1. Параметры для расчёта
| Напряжение питания цепи, В | Резистивное сопротивление катушки, Ом | Индуктивность катушки, Гн |
| 12 | 100 | 0,15 |
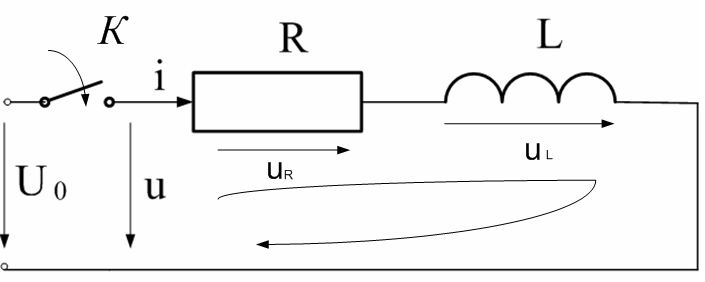
Рис.5.1. Электрическая цепь с последовательным соединением резистора и катушки индуктивности
При выполнении задания рекомендуется использовать метод уравнений состояния переходного процесса при подключении катушки индуктивности к источнику постоянного напряжения:
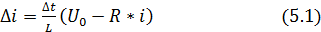
При моделировании необходимо правильно выбрать величину шага квантования. Чем меньше эта величина, тем меньше будет ошибка интегрирования.
|
|
|
Выбор величины шага квантования определяется теоремой Котельникова-Шеннона (1.4), где 
Тогда шаг квантования с применением расчёта эмпирической формулы будет равен:
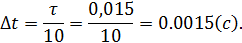
Заносим все данные в Microsoft Excel.
Расчёт начинаем с того, что в соответствующие ячейки памяти ЭТ Excel записываются следующие величины:
Рис.5.2. Данные для расчёта электрической цепи с катушкой индуктивности
Заполняем столбец «t» - записываем все значения, начиная с 0, с шагом равным 
Столбец «deltai» заполняем с помощью формулы «=$J$2/$H$2*($F$2-$G$2*B2)». Столбец «ik» начинаем заполнять с 0, прибавляя к последующей ячейке значение «ik» - «=B2+C2». Столбец «uL» с помощью формулы – «=$H$2*C2/$J$2».
Рис.5.3. Рассчитанные значения
По данным значениям строим графики зависимости напряжения и тока от времени.
Рис.5.4. График зависимости напряжения на индуктивном элементе от времени
Рис.5.5. График зависимости тока в цепи с индуктивным элементом от времени
