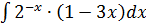 .
.
Решение:
Теоретический минимум
________________________________________________
Для вычисления данного интеграла мы применим метод интегрирования по частям.
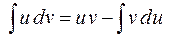 - формула интегрирования по частям.
- формула интегрирования по частям.
Формула применяется, когда подынтегральное выражение можно представить в виде произведения двух множителей 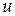 и
и  так, чтобы отыскание функции
так, чтобы отыскание функции 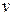 по ее дифференциалу и вычисление интеграла
по ее дифференциалу и вычисление интеграла 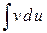 составляли в совокупности задачу более простую, чем вычисление интеграла
составляли в совокупности задачу более простую, чем вычисление интеграла 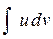 .
.
В подынтегральном выражении за 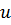 рекомендуют брать многочлены,
рекомендуют брать многочлены, 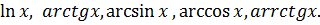
________________________________________________
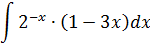
Подынтегральная функция представляет собой произведение функции 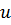 на дифференциал
на дифференциал  . Согласно рекомендациям за
. Согласно рекомендациям за 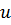 следует взять
следует взять 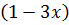 . Тогда
. Тогда 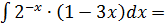
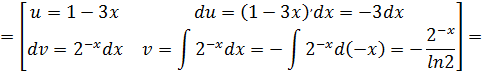
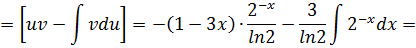
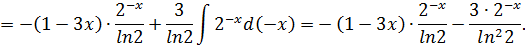
Ответ:
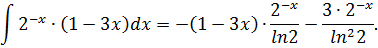
Задание 2.3.
Вычислить неопределенный интеграл
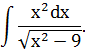
Решение:
Теоретический минимум
________________________________________________
Для вычисления данного интеграла мы применим метод замены переменной:
Таблица 2. Интегралы от иррациональных функций
| Тип интеграла | Замена переменной |
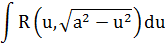
| 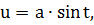
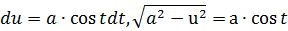
|
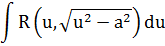
| 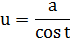
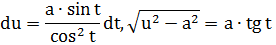
|
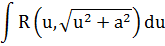
| 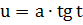
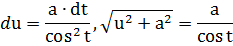
|
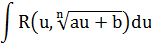
| 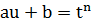
|
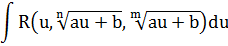
| 
|
________________________________________________
Данный нам интеграл
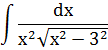
относится ко второму виду. Используем замену  . Тогда
. Тогда
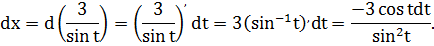
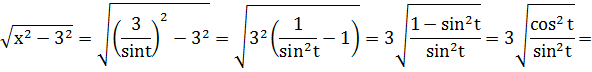
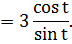
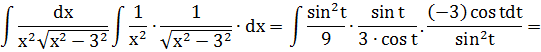
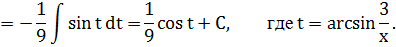
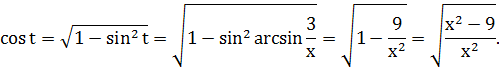
Ответ:
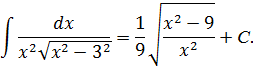
 2020-04-07
2020-04-07 79
79








