2020-04-12
310
С точки зрения закона сохранения энергии принцип работы электродвигателя прост. Электрическая энергия, потребляемая из сети (или от источника тока) переходит в механическую энергию. Каким образом это происходит? В простейшем варианте двигатель представляет собой катушку или рамку с током (якорь двигателя), помещенную в магнитное поле, создаваемое электромагнитом (индуктором двигателя). Подвижная часть двигателя называется ротором, а неподвижная – статором. Роли ротора и статора исполняют якорь и индуктор. На проводник с током в магнитном поле действует сила Ампера. Очевидно, именно она и вращает или перемещает якорь электродвигателя, совершая при этом работу.
|
Определим работу по перемещению или деформации контура с постоянным электрическим током в магнитном поле. Рассмотрим простой частный случай контура АВСD с током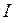 
, одна из сторон которого СD представляет собой подвижную перемычку (рис. 3.16), которая играет роль якоря. Контур находится в однородном постоянном магнитном поле с индукцией 
(направленном на нас перпендикулярно плоскости листа), создаваемом некоторым индуктором. На перемычку CD длиной 
действует сила Ампера 
и она начнет движение. При перемещении перемычки контур деформируется – его площадь становится больше.
Пусть перемычка CD переместилась на расстояние 
. Тогда сила Ампера совершит работу 
. Или, учитывая, что 
- приращение площади контура, получим 
. Величина 
представляет собой приращение магнитного потока 
, пронизывающего контур ABCD. Таким образом, работа силы Ампера, совершенная при деформации контура,
. (3.22)
Формула (3.22) получена нами в частном случае. Отметим, однако, что можно строго доказать справедливость этой формулы и для любого контура с постоянным током при произвольном его перемещении или деформации в неоднородном постоянном поле. Например, формулой (3.22) можно воспользоваться при вычислении работы магнитного поля (или другими словами работы силы Ампера), совершаемой при повороте рамки с постоянным током в однородном магнитном поле:
,
где 
и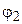 
- углы, которые составляет нормаль к плоскости рамки с направлением вектора магнитной индукции в начальном и конечном положении. Учитывая, что магнитный момент рамки 
, получим:
.
Если рамка поворачивается из устойчивого положения равновесия, то 
и
.
На первый взгляд проблема, обсуждаемая в настоящем разделе, может показаться решенной. Сила Ампера приводит в движение ротор двигателя, ее работа рассчитывается по формуле (3.22). Но в разделе 3.3 мы говорили о том, что сила Ампера, действующая на проводник с током, представляет собой сумму всех сил Лоренца, действующих на каждый свободный электрон в проводнике. А работа силы Лоренца всегда равна нулю (см. п. 3.1). Каким образом тогда может быть отличной от нуля работа силы Ампера?
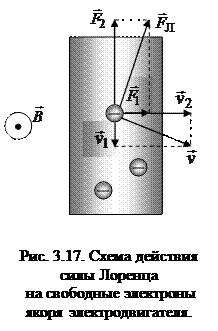
Рассмотрим еще раз движущийся проводник (якорь) с током (перемычка CD на рис. 3.16). По проводнику течет ток 
снизу вверх, следовательно, электроны движутся упорядоченно сверху вниз с некоторой скоростью 
относительно проводника. Поскольку сам проводник движется с некоторой скоростью 
слева направо, результирующая скорость электрона 
направлена под некоторым углом к проводнику (рис. 3.17). Сила Лоренца 
перпендикулярна скорости 
, и ее работа будет действительно равна нулю. Однако силу Лоренца, как и любую другую силу, можно разложить на две составляющие, действующие вдоль провода и перпендикулярно ему: 
. Сила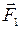 
направлена перпендикулярно проводу по направлению его перемещения, т.е. совершает положительную работу. Такая сила действует на каждый электрон в проводе. Именно сумму всех сил 
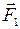мы называли силой Ампера при выводе формулы для работы, совершаемой магнитным полем по перемещению якоря двигателя (формула (3.22)). Составляющая 
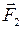тормозит электроны и совершает отрицательную работу. В результате суммарная работа сил 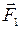и 
, т.е. работа силы Лоренца, как и полагается, равна нулю.
|
Работа силы 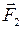привела бы к остановке электронов и прекращению тока, если бы еще одну положительную работу не совершал источник тока. Напряжение источника поддерживает ток в проводе, несмотря на торможение, вызванное силой 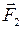и наличие сопротивления провода. В результате, в конечном счете, электродвигатель работает за счет энергии источника тока. За счет работы источника совершается механическая работа (вращается ротор) и нагревается обмотка электродвигателя. Закон сохранения энергии для электродвигателя можно записать следующим образом:
,
где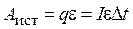 
- работа источника тока с ЭДС 
, 
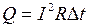- тепло, выделяющееся в обмотке (
– общее сопротивление цепи), 
- механическая работа, равна работе силы Ампера (составляющих силы Лоренца 
). Получим:
.
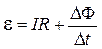Таким образом, сила тока, текущая через якорь электродвигателя, определяется выражением:
.
Этот результат можно трактовать так: при изменении магнитного потока, пронизывающего замкнутый контур с током (якорь), в контуре, помимо действия ЭДС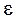 
, возникает дополнительная ЭДС, равная 
(работа этой ЭДС есть, конечно, работа составляющих сил Лоренца 
). Эту дополнительную ЭДС называют ЭДС индукции и обозначают 
. В итоге можно записать
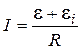, где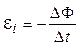 
.
Об ЭДС индукции и причинах её возникновения пойдет речь в последующих разделах.
Индуктивность
Пусть в некотором контуре течет ток . Этот ток создает в окружающем пространстве магнитное поле. Силовые линии магнитного поля пронизывают данный контур, и имеет место магнитный поток. Магнитный поток через контур, созданный током самого контура называется собственным магнитным потоком контура. Величина магнитного поля, создаваемого каждым небольшим элементом контура согласно закону Био-Савара-Лапласа прямо пропорциональна току 
. Следовательно, магнитная индукция 
в каждой точке пространства прямо пропорциональна току, а значит и собственный магнитный поток всегда прямо пропорционален току. Таким образом, можно записать:
, (3.23)
где 
- некоторый коэффициент пропорциональности. Этот коэффициент пропорциональности между собственным магнитным потоком и током называется индуктивностью. В СИ индуктивность измеряется в Генри (Гн).
Индуктивность контура зависит от геометрических характеристик контура и магнитных свойств среды, в которой находится данный контур.
Рассчитаем, например, индуктивность длинного соленоида без сердечника. Магнитное поле внутри длинного соленоида (см. формулу (3.18) и пример 3.7)
,
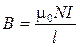причем силовые магнитные линии параллельны оси соленоида. Следовательно, полный собственный магнитный поток соленоида
.
Сравнение с формулой (3.23) дает:
. (3.24)
В заключение отметим, что наличие ферромагнитного сердечника, безусловно, скажется на величинах магнитного поля и магнитного потока, пронизывающего витки соленоида. Это значит, что изменится и индуктивность. Этого вопроса мы еще коснемся в дальнейшем, а пока отметим, что причина зависимости индуктивности от вещества сердечника – намагниченность вещества. В результате вещество создает дополнительное магнитное поле, складывающееся с полем, создаваемым током, текущим по виткам соленоида.
