Фазовым называют транспарант, который определённым образом изменяет фазу падающей на него волны. Рассмотрим два частных случая фазовых транспарантов – линейный и квадратичный.
Дифракция Фраунгофера на линейном фазовом транспаранте.
Физической реализацией линейного фазового транспаранта является оптический клин (рис. 7.38). Пусть на оптический клин с показателем преломления  , малым углом
, малым углом  при вершине и размером 2a падает по нормали к поверхности плоская волна с амплитудой
при вершине и размером 2a падает по нормали к поверхности плоская волна с амплитудой  . Без учёта отражения и преломления излучения в клине поле U
. Без учёта отражения и преломления излучения в клине поле U  на выходе из транспаранта имеет вид:
на выходе из транспаранта имеет вид:
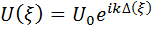 , (7.64)
, (7.64)
где
 (7.65)
(7.65)
– оптическая длина хода участка волнового фронта волны с координатой  .
.
Рис. 7.38 Линейный фазовый транспарант
С учётом (7.64) и (7.65) дифракционный интеграл Фраунгофера имеет вид:
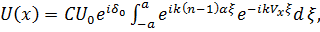 (7.66)
(7.66)
где
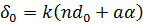
– фаза, зависящая от параметров клина. Обозначим  множитель перед интегралом (7.66), получим
множитель перед интегралом (7.66), получим
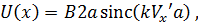
где
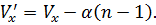
Последние равенства означают, что поле, дифрагированное на линейном фазовом транспаранте с точностью до постоянной совпадает с полем при дифракции на щели шириной 2 а, однако смещено на величину
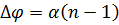
к основанию клина. Этот результат полностью совпадает с известным положением геометрической оптики, согласно которому луч, падающий на клин с малым углом 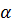 при вершине, отклоняется к основанию на угол
при вершине, отклоняется к основанию на угол 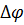 .
.
Дифракция Френеля на квадратичном фазовом транспаранте.
Физической реализацией такого транспаранта является линза. На рисунке 7.39 представлена линза с показателем преломления n и радиусами  и
и  . Определим оптическую длину луча, идущего на высоте
. Определим оптическую длину луча, идущего на высоте  .
.
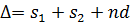 ,
,
где 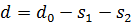 .
.
Рис. 7.39 Линза как квадратичный фазовый транспарант
Здесь  – толщина линзы на оси;
– толщина линзы на оси;  – стрелки прогиба.
– стрелки прогиба.
При условии 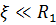 , и
, и  с точностью до квадратичных членов по
с точностью до квадратичных членов по  .
.

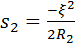 .
.
Следовательно
 ,
,
где 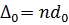 ,
,
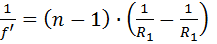 — оптическая сила линзы.
— оптическая сила линзы.
Рассмотрим задачу определения поля, сформированного линзой (рис. 7.40).
Рис. 7.40 Дифракция Френеля на квадратичном транспаранте
Пусть в плоскости  задано распределение поля
задано распределение поля 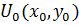 . Тогда из (19) получим, что распределение поля в плоскости
. Тогда из (19) получим, что распределение поля в плоскости 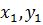 будет равно
будет равно
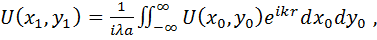 (7.67)
(7.67)
где 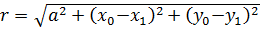 .
.
Рассмотрим задачу в одномерном приближении, тогда (7.67) принимает вид:
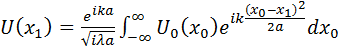 . (7.68)
. (7.68)
Здесь учтено, что в приближении Френеля

Поле после линзы с учётом изменения фазы
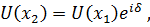 (7.69)
(7.69)
где  .
.
Поле в плоскости 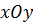 по аналогии с (7.68) имеет вид:
по аналогии с (7.68) имеет вид:
 (7.70)
(7.70)
Подставляя в (7.70) последовательно (7.69) и (7.68) получаем
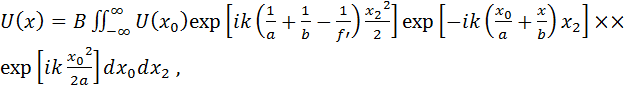 (7.71)
(7.71)
где  — постоянный коэффициент.
— постоянный коэффициент.
Интеграл по  табличный, поэтому после интегрирования по
табличный, поэтому после интегрирования по 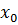 можно получить значения поля
можно получить значения поля 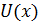 в любой точке.
в любой точке.
Потребуем, чтобы плоскости 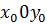 и
и 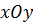 были оптически сопряжёнными, т.е. выполнялось соотношение:
были оптически сопряжёнными, т.е. выполнялось соотношение:  . Тогда (7.71) принимает вид:
. Тогда (7.71) принимает вид:
 (7.72)
(7.72)
При этом учтено, что

Используя фильтрующее свойство δ-функции:
 ,
,
из (7.72) получаем
 .
.
Последнее выражение показывает, что поле в плоскости 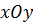 подобно полю в плоскости
подобно полю в плоскости 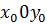 с коэффициентом подобия
с коэффициентом подобия  , равным линейному увеличению линзы. В двумерном случае поля в оптически сопряжённых плоскостях с точностью до константы C связаны соотношением:
, равным линейному увеличению линзы. В двумерном случае поля в оптически сопряжённых плоскостях с точностью до константы C связаны соотношением:
 . (7.73)
. (7.73)
Аналогичным образом связаны между собой интенсивности света в этих плоскостях:
 .
.  (7.74)
(7.74)
Соотношения (7.73) и (7.74) дают возможность определять поля и их интенсивности в оптически сопряжённых плоскостях оптической системы. Например, если линза преобразует лазерный пучок излучения, а плоскости  и
и  являются оптически сопряжёнными, то распределение интенсивностей света в них определяется соотношением (7.74).
являются оптически сопряжёнными, то распределение интенсивностей света в них определяется соотношением (7.74).
Задачи и примеры
Задача1. Рассчитать фазовую бинарную пластинку Френеля радиуса 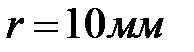 , изготовленную из стекла с показателем преломления
, изготовленную из стекла с показателем преломления  , проецирующую точечный монохроматический
, проецирующую точечный монохроматический 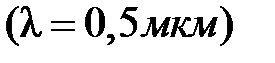 источник света Po, находящийся на расстоянии -
источник света Po, находящийся на расстоянии - 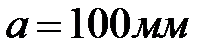 от пластинки в точку P, находящуюся от неё на расстоянии
от пластинки в точку P, находящуюся от неё на расстоянии 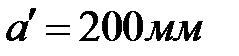 .
.
В ходе расчёта найти:
— общее число зон Френеля;
— радиус отдельной j -ой зоны Френеля;
— глубину травления четных зон бинарной фазовой пластинки;
— наименьшую ширину зоны Френеля.
Решение
Общее число N зон Френеля найдем из условия:  ,
,
где  и
и  – стрелки прогиба радиусов
– стрелки прогиба радиусов  и
и  на радиусе r пластинки. С учётом формулы (7.15), получаем:
на радиусе r пластинки. С учётом формулы (7.15), получаем:
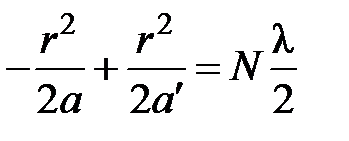 .
.
Отсюда
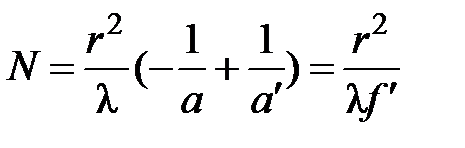 ,
,
где 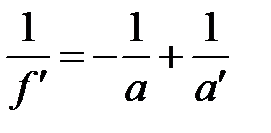 — оптическая сила зонной пластинки.
— оптическая сила зонной пластинки.
Отсюда можно определить радиус отдельной зоны Френеля
 ,
,
где j=1,2,…N.
Глубина травления h должна обеспечивать скачок фазы на π или разность хода  для соседних зон, т.е.
для соседних зон, т.е.  . Отсюда
. Отсюда
 .
.
Площадь каждой зоны  Френеля одинакова, т.е. не зависит от номера зоны. Действительно
Френеля одинакова, т.е. не зависит от номера зоны. Действительно 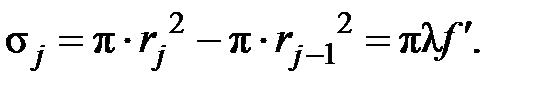
Наименьшую ширину 
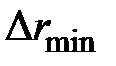 имеет, следовательно, последняя N -ая зона. Она определяется из условия:
имеет, следовательно, последняя N -ая зона. Она определяется из условия: 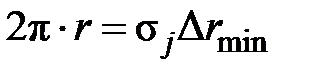 .
.
Отсюда
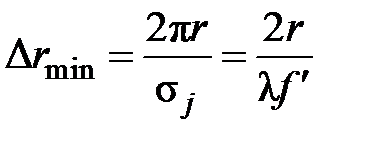 .
.
Задача 2. С помощью дифракционного интеграла Френеля определить интенсивность  излучения на оси отверстия радиуса r=a, освещаемого плоской волной (рис. 7.9). Длина волны -
излучения на оси отверстия радиуса r=a, освещаемого плоской волной (рис. 7.9). Длина волны -  . Показать, что максимумы функции
. Показать, что максимумы функции  совпадают с точками zi, в которых в отверстии укладывается нечётное число зон Френеля.
совпадают с точками zi, в которых в отверстии укладывается нечётное число зон Френеля.
Решение
Дифракционный интеграл в приближении Френеля имеет вид:

В точке Р на оси отверстия x=y=0 и после перехода к полярной системе координат интеграл принимает вид:

Интенсивность в точке Р:
 ,
,
где  .
.
Из последнего выражения следует, что в точках
а) 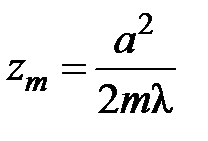 , где m=1, 2, 3….,
, где m=1, 2, 3….,  ,
,
а в точках
б)  , где m=1, 2, 3….,
, где m=1, 2, 3…., 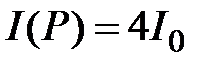 .
.
Условию а) отвечают, очевидно, точки на оси с координатами  , из которых в отверстии наблюдается чётное, а условию б) нечётное число зон Френеля.
, из которых в отверстии наблюдается чётное, а условию б) нечётное число зон Френеля.
Задача 3 Показать, что если отверстие радиуса а из задачи 2 заменить непрозрачным кругом того же радиуса, то интенсивность в центре геометрической тени будет равна I0.
Решение. Поле в точке Р в отсутствие экранов и диафрагм равно 
При наличии экрана по принципу Бабине имеем: 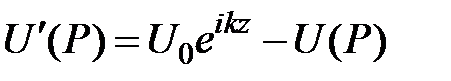 ,
,
где  – поле в точке Р от отверстия. С учётом формулы (1) получаем
– поле в точке Р от отверстия. С учётом формулы (1) получаем

Интенсивность в точке Р: 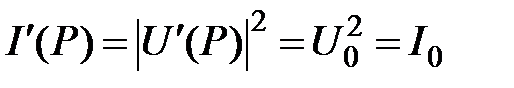 .
.
Задача 4. Определить поле, дифрагированное на транспаранте (рис. 7.41), в области Фраунгофера (дальняя зона дифракции) при освещении его плоской волной с амплитудой U0. Определить интенсивность дифрагированного света. Амплитудное пропускание транспаранта описывается функцией: 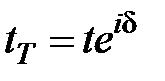 .
.
Рис.7.41 К задаче 4
Решение. Искомое поле в плоскости, отстоящей от транспаранта на расстояние z, определяем по принципу суперпозиции следующим образом:
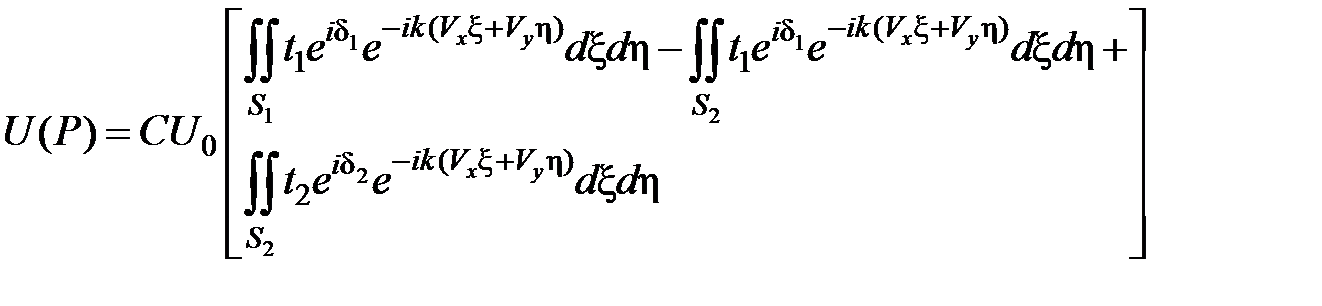 ,
,
где
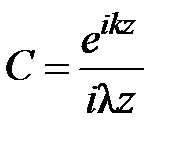 ,
, 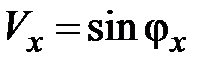 ,
,  .
.
После подстановки исходных данных и преобразований получим:
 ,
,
где  .
.
Интенсивность дифрагированного света
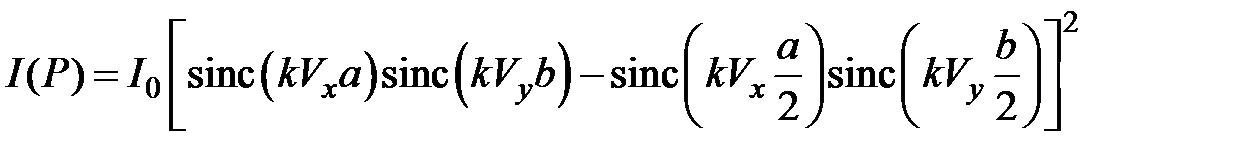 ,
,
где 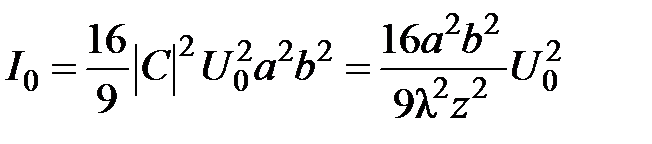 .
.
Отметим, что в центре дифракционного кружка (x=0, y=0) интенсивность света равна нулю.
Задача 5. Показать, что при дифракции света на амплитудной решётке с параметрами 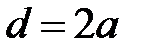 интенсивность всех чётных максимумов равна нулю.
интенсивность всех чётных максимумов равна нулю.
Решение. Интенсивность света при дифракции на решётке равна 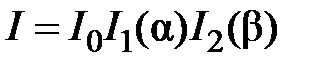 , где
, где  ,
,  .
.
Здесь 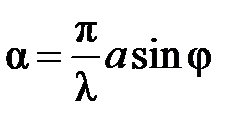 ,
,  .
.
Положение главных максимумов функции 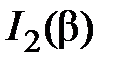 определяется соотношением:
определяется соотношением:
 то есть
то есть  где
где  . Для чётных максимумов
. Для чётных максимумов  имеем:
имеем:  и тогда
и тогда 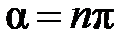 . Поскольку
. Поскольку 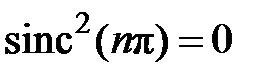 , то
, то  , следовательно интенсивность всех четных максимумов равна нулю.
, следовательно интенсивность всех четных максимумов равна нулю.
Задача 6 Отражательная дифракционная решётка размером L=100 мм освещается по нормали ( = 0). Решётка работает в 3-ем порядке (m=3) при угле блеска
= 0). Решётка работает в 3-ем порядке (m=3) при угле блеска  б = 30°. Спектральный диапазон
б = 30°. Спектральный диапазон  = 500...700 нм. Определить параметры
= 500...700 нм. Определить параметры 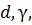 N и характеристики
N и характеристики 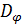 и
и  решётки, при которых для средней длины волны
решётки, при которых для средней длины волны  ср = 600 нм. разрешающая способность R = 3
ср = 600 нм. разрешающая способность R = 3  104
104
Решение: Разрешающая способность решётки  , откуда спектральный предел разрешения
, откуда спектральный предел разрешения  = 0.02 нм. Угловая дисперсия
= 0.02 нм. Угловая дисперсия 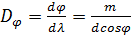 . Кроме того, имеем
. Кроме того, имеем  , отсюда
, отсюда  .
.
Поскольку 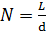 , отсюда
, отсюда  мкм.
мкм.
Угол блеска определяется выражением:
d(sin  б + sin
б + sin  ) =
) = 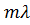 , отсюда при
, отсюда при  = 0
= 0
sin  б =
б =  =
= 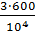 = 0,18;
= 0,18;  б = 10,4°, т.к.
б = 10,4°, т.к.  б =
б = 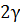 ,
, 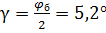
Вопросы для самоконтроля
1. Сформулируйте принцип Гюйгенса-Френеля.
2. Чем отличаются амплитудная и фазовая зонные пластинки Френеля?
3. Что такое дальняя зона дифракции?
4. Что такое оптическое приближение в дифракционном интеграле Кирхгофа?
5. Как определяются области дифракции Френеля и Фраунгофера?
6. Как изменяются поле и его интенсивность в области дифракции Фраунгофера при смещении транспаранта?
7. Напишите основное уравнение дифракционной решётки. Что оно определяет?
8. Чем отличаются спектры синусоидальной и дискретной дифракционных решёток?
9. Что такое амплитудный и фазовый транспаранты?
10. Какова особенность дифракции света на линейном фазовом транспаранте?
11. Квадратичный фазовый транспарант; его реализация. Особенность дифракции на этом транспаранте.
12. Сформулируйте принцип Бабине.
[*] вектор 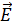 сферической волны, исходящей из точки P0 равен
сферической волны, исходящей из точки P0 равен 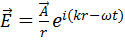 . В скалярной теории дифракции обозначения векторов и член
. В скалярной теории дифракции обозначения векторов и член  опускают.
опускают.
[†] Ниже при рассмотрении теории дифракции Кирхгофа будет получено строгое выражение для углового коэффициента 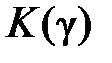 .
.
 2020-04-12
2020-04-12 478
478







