Пусть на транспарант представляющий собой круг радиуса a, по нормали падает плоская волна, амплитуда колебаний которой в плоскости отверстия равна U (ξ,η) (рис. 7.28).
Введем полярные координаты ρ, α и r, β в плоскостях ξ, η и x,y, соответственно. Тогда можно записать формулы:
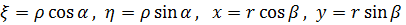 .
.
Рис. 7.28 Полярные координаты в плоскостях отверстия (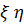 ) и анализа (
) и анализа (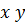 )
)
Подставив эти переменные в дифракционный интеграл Фраунгофера (7.40), получим:
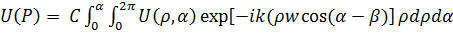 , (7.53)
, (7.53)
где
C= 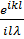 ,
, 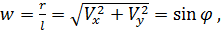 (рис. 7. 29)
(рис. 7. 29)
Рис. 7.29 Дифракция Фраунгофера на круглом отверстии
Если функция U(ρ,α) зависит только от радиальной координаты отверстия, т.е. U(ρ,α)=U(ρ), то воспользовавшись хорошо известным представлением функции Бесселя первого рода нулевого порядка
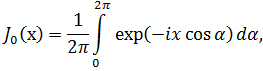
интеграл (7.53) можно представить в следующем виде:
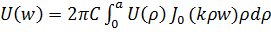 (7.54)
(7.54)
Последнее выражение c точностью до постоянной 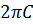 представляет собой одномерное преобразование Фурье-Бесселя или преобразование Ханкеля нулевого порядка от функции
представляет собой одномерное преобразование Фурье-Бесселя или преобразование Ханкеля нулевого порядка от функции 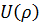 , в котором пространственная частота
, в котором пространственная частота 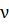 определяется выражением:
определяется выражением:
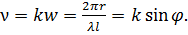 (7.55)
(7.55)
Таким образом, поле в дальней зоне при дифракции на круглом отверстии с точностью до постоянной равно преобразованию Фурье-Бесселя от осесимметричного распределения поля на транспаранте.
Если в пределах транспаранта можно считать, что
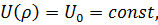
то
U(w)= 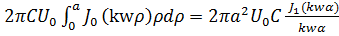 ,
,
где 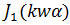 – функция Бесселя первого рода первого порядка. В последнем выражении мы использовали табличный интеграл
– функция Бесселя первого рода первого порядка. В последнем выражении мы использовали табличный интеграл
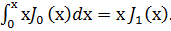
Распределение интенсивности дифрагированного света в дальней зоне
I(w)= 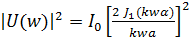 ,
,
где 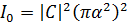 .
.
График функции 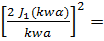 I(w)/
I(w)/ 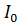 представлен на рисунке 7.30.
представлен на рисунке 7.30.
Рис 7.30 Распределение интенсивности в дальней зоне при дифракции на круглом отверстии
Из графика следует, что распределение интенсивности в дифракционном кружке представляет собой главный максимум, окружённый слабыми дополнительными концентрическими максимумами, интенсивности которых составляют 0,0175 и 0,0042 от интенсивности главного. Это распределение получило название кружка Эри. Радиус ближайшего тёмного кольца определяется условием k 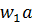 =3,83.
=3,83.
Отсюда можно определить угловой размер центрального максимума.
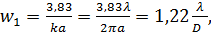 (7.56)
(7.56)
где D=2a – диаметр транспаранта.
Формула (7.56) согласно критерию Релея определяет дифракционную разрешающую способность идеального объектива со световым диаметром D. Если на такой объектив с фокусным расстоянием f’ падает свет от двух удалённых точек одинаковой интенсивности, находящихся на угловом расстоянии 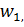 то в фокальной плоскости объектива будут наблюдаться два кружка Эри, центры которых отстают друг от друга на расстояние
то в фокальной плоскости объектива будут наблюдаться два кружка Эри, центры которых отстают друг от друга на расстояние 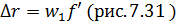 .
.
Рис 7.31 Предельное разрешение точек согласно критерию Релея
При этом в суммарном распределении интенсивности между кружками наблюдается значительный перепад, составляющий примерно было 20% от интенсивности каждого главного максимума.
Этот перепад позволяет надёжно судить о наличии двух источников света. При меньшем угловом расстоянии между источниками перепада в суммарном распределении интенсивности не будет, и разрешение точек становится проблематичным.
7.5.7 Дифракционная решётка
Рассмотрим дифракцию света на амплитудной решётке, представляющей собой систему эквидистантных щелей шириной а, расстояния между которыми равно d (рис. 7.32), N - общее число штрихов решётки. Пусть амплитуда падающей плоской волны 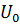 , тогда дифракция Фраунгофера на одной щели определяется выражением (7.49), а именно:
, тогда дифракция Фраунгофера на одной щели определяется выражением (7.49), а именно:
Рис. 7.32 К дифракции света на решётке
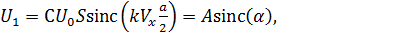 (7.57)
(7.57)
где
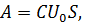
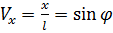 , S –площадь щели;
, S –площадь щели; 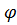 – угол дифракции;
– угол дифракции;
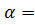
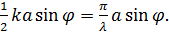
Поскольку дифрагированная в направлении 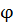 волна от второй щели отстает по фазе от колебаний первой щели на величину
волна от второй щели отстает по фазе от колебаний первой щели на величину
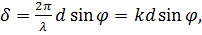 (7.58)
(7.58)
то поле от второй щели можно записать в виде:
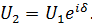
Аналогично для амплитуды поля от j-ой щели имеем
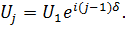
Общее поле в дальней зоне дифракции определяется суммой
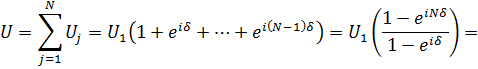
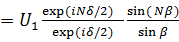 ,
,
где
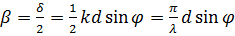 .
.
C учётом (7.57) окончательно получим:
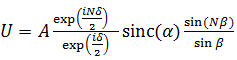 (7.59)
(7.59)
Для интенсивности дифрагированного поля получим:
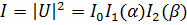 , (7.60)
, (7.60)
где
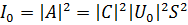
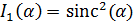 ,
,
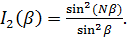
Вид функции 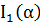 в зависимости от аргумента
в зависимости от аргумента 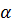 хорошо известен.
хорошо известен.
Рассмотрим более подробно функцию 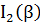 (рис. 7.33).
(рис. 7.33).
При 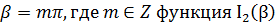 имеет неопределенность типа «
имеет неопределенность типа «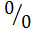 », раскрыв которую, получаем
», раскрыв которую, получаем 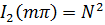 . В этих точках функция
. В этих точках функция 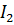 имеет максимальное значение – главные максимумы. Угловое положение главных максимумов легко находится из (7.60):
имеет максимальное значение – главные максимумы. Угловое положение главных максимумов легко находится из (7.60):
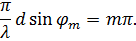
Отсюда имеем уравнение
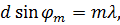 (7.61)
(7.61)
которое называется основным уравнением дифракционной решётки, а m=0, ±1, ±2 … – порядком дифракции. Между главными максимумами функция 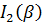 имеет N-1 минимум, в которых она принимает нулевое значение и N-2 побочных максимума. Отметим, что минимумы наблюдаются при условиях
имеет N-1 минимум, в которых она принимает нулевое значение и N-2 побочных максимума. Отметим, что минимумы наблюдаются при условиях
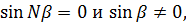
а интенсивность побочных максимумов значительно меньше интенсивности главных. На рисунке 7.33 изображена функция 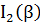 при N =6 и интенсивности побочных максимумов в 20 раз меньше интенсивности главных. На практике N исчисляется тысячами, десятками и даже сотнями тысяч штрихов, поэтому интенсивность побочных максимумов незначительна и можно считать, что вся энергия дифрагированного света сосредоточена в главных максимумах.
при N =6 и интенсивности побочных максимумов в 20 раз меньше интенсивности главных. На практике N исчисляется тысячами, десятками и даже сотнями тысяч штрихов, поэтому интенсивность побочных максимумов незначительна и можно считать, что вся энергия дифрагированного света сосредоточена в главных максимумах.
Причиной такого перераспределения энергии в пространстве является интерференция света от всех штрихов решётки. Действительно из выражения (7.61) и (7.58) следует, что волны, идущие от всех штрихов решётки в направлениях 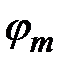 складываются в фазе, что соответствует максимуму интерференции. На том же рисунке (7.33 б) приведён график функции
складываются в фазе, что соответствует максимуму интерференции. На том же рисунке (7.33 б) приведён график функции 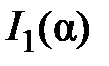 для случая а=
для случая а= 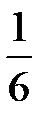 d. Эта функция характеризует дифракцию света на одной щели решётки. На рисунке 7.33 в) представлен результирующий график интенсивности дифрагированного света.
d. Эта функция характеризует дифракцию света на одной щели решётки. На рисунке 7.33 в) представлен результирующий график интенсивности дифрагированного света.
Из представленных графиков видно, что не все главные максимумы имеют одинаковую интенсивность, наибольшую интенсивность имеет главный максимум нулевого порядка, а главный максимум 6-го порядка, наложившись на ноль функции 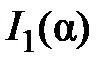 , вообще принимает нулевое значение.
, вообще принимает нулевое значение.
Рис. 7.33 Характер функций 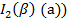 ,
, 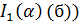 ,
, 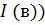
 2020-04-12
2020-04-12 396
396








