2020-04-12
205
Написать краткий конспект и выполнить задания для самостоятельного решения по вариантам(номер варианта смотреть по фото журнала в беседе)
Цель: научиться записывать числовые последовательности различными способами, описывать их свойства; находить пределы последовательностей и функций.
Краткая теория
Функция у=f (n) натурального аргумента n (n=1; 2; 3; 4;...) называется числовой последовательностью.
Существуют следующие способы задания числовой последовательности:
1) Словесный способ. Представляет собой закономерность или правило расположения членов последовательности, описанный словами.
2) Аналитический способ. Последовательность задается формулой n-го члена: уn=f(n). По этой формуле можно найти любой член последовательности.
3) Рекуррентный способ. Задается формула, по которой каждый следующий член находят через предыдущие члены. В случае рекуррентного способа задания функции всегда дополнительно задается один или несколько первых членов последовательности.
|
|
|
Числовую последовательность называют возрастающей, если ее члены возрастают (уn+1>уn) и убывающей, если ее члены убывают (уn+1<уn).
Возрастающая или убывающая числовые последовательности называются монотонными.
Пусть 
– точка прямой, а 
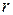– положительное число. Интервал 
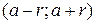называется окрестностью точки , а число 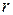− радиусом окрестности.
Рассмотрим числовую последовательность, общий член которой приближается к некоторому числу b при увеличении порядкового номера n. В этом случае говорят, что числовая последовательность имеет предел. Это понятие имеет более строгое определение.
Число b называют пределом последовательности (уn), если в любой заранее выбранной окрестности точки b содержат все члены последовательности, начиная с некоторого номера
.
Теорема 1 Если 
, 
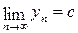, то:
1) Предел суммы/разности двух последовательностей равен сумме/разности пределов от каждой из них, если последние существуют:
;
2) Предел произведения двух последовательностей равен произведению пределов от каждой из них, если пределы сомножителей существуют:
;
3) Предел отношения двух последовательностей равен отношению пределов от каждой из них, если эти пределы существуют и предел знаменателя не равен нулю:
;
4) Постоянный множитель можно вынести за знак предела:
.
Для любого натурального показателя m и любого коэффициента k справедливо соотношение:
.
Для любого натурального показателя m и любого коэффициента k справедливо соотношение:
.
Теорема 1 Если 
, 
, то:
1) Предел суммы/разности двух функций равен сумме/разности пределов от каждой из них, если последние существуют:
|
|
|
;
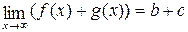2) Предел произведения двух функций равен произведению пределов от каждой из них, если пределы сомножителей существуют:
;
3) Предел отношения двух функций равен отношению пределов от каждой из них, если эти пределы существуют и предел знаменателя не равен нулю:
;
4) Постоянный множитель можно вынести за знак предела:
.
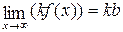Функцию у=f(x) называют непрерывной в точке x=a, если предел функции у=f(x) при стремлении x к a равен значению функции в точке х=а.
.
