Однородность пространства означает, что перенос системы вдоль определенного направления в пространстве не меняет ее состояния. При таком переносе все координаты микрочастиц 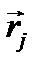 (считаем, что их N, поэтому j = 1, 2, …, N), из которых состоит система, получают одно и тоже приращение
(считаем, что их N, поэтому j = 1, 2, …, N), из которых состоит система, получают одно и тоже приращение 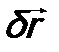 . Рассмотрим, как будет при таком переносе изменяться волновая функция системы
. Рассмотрим, как будет при таком переносе изменяться волновая функция системы 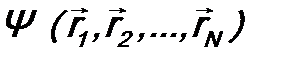 (принимаем, что
(принимаем, что 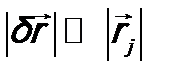 , j = 1, 2, …, N).
, j = 1, 2, …, N). 
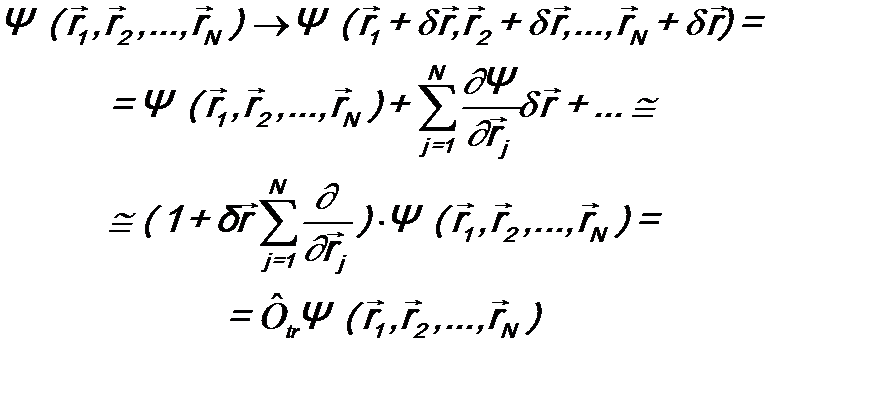 ,
,
где оператор
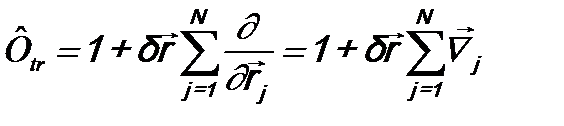 (14.2)
(14.2)
можно назвать оператором параллельного переноса системы частиц (оператор трансляции – это отражено индексом “ tr ”). Так как пространство однородно, то волновая функция 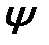 и преобразованная волновая функция
и преобразованная волновая функция 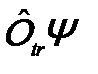 описывают одно и тоже состояние. Поэтому можно написать:
описывают одно и тоже состояние. Поэтому можно написать: 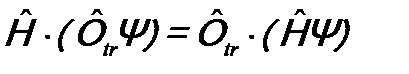 , или
, или 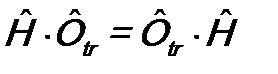 .
.
Подставляя сюда оператор 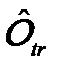 в виде (14.2), получим:
в виде (14.2), получим:
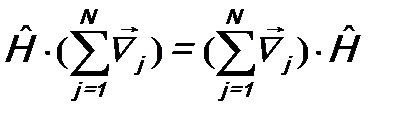 .
.
Как отмечалось выше, если некоторый оператор коммутирует с гамильтонианом, то должен быть соответствующий этому оператору интеграл состояния. Дадим определение:
физическая величина, сохранение которой есть следствие однородности пространства, называется импульсом.
В данном случае это будет импульс системы из N микрочастиц. Его оператор имеет вид:
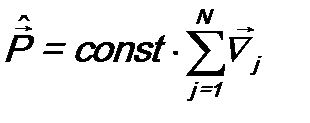 .Если ввести оператор импульса микрочастицы
.Если ввести оператор импульса микрочастицы  , то
, то 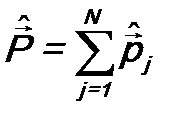 . Следовательно, соответствующая физическая величина – импульс системы частиц, как и оператор, будет аддитивна, т.е. будет суммой импульсов отдельных частиц. Действительно, этим физическим свойством обладает импульс системы частиц.
. Следовательно, соответствующая физическая величина – импульс системы частиц, как и оператор, будет аддитивна, т.е. будет суммой импульсов отдельных частиц. Действительно, этим физическим свойством обладает импульс системы частиц.
Для нахождения величины константы можно воспользоваться предельным переходом от квантовой механики к классической. Формально этот переход осуществляется в виде предела 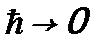 . В этом случае действие оператора на волновую функцию сводится просто к умножению ее на соответствующую физическую величину, т.е.
. В этом случае действие оператора на волновую функцию сводится просто к умножению ее на соответствующую физическую величину, т.е.
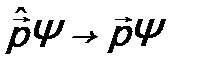 , (14.3)
, (14.3)
а сама волновая функция принимает вид: 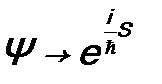 , где S – действие. Используем ее:
, где S – действие. Используем ее:
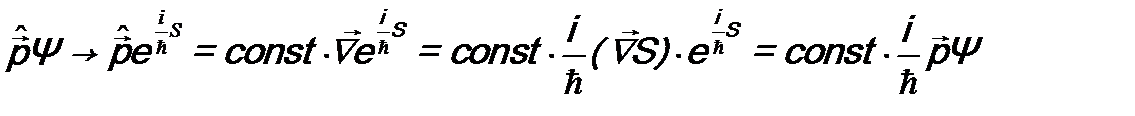 .
.
Учтено, что в классической механике 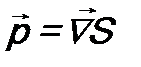 . Сравнение с соотношением (12.3) показывает:
. Сравнение с соотношением (12.3) показывает: 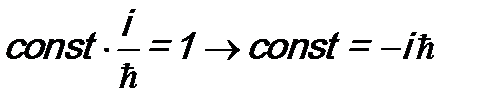 .
.
В результате оператор импульса принимает уже известный вид (см. ф-лу (7.2)): 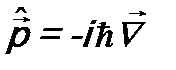 . Соответственно получаем уравнение на собственные функции и собственные значения оператора импульса:
. Соответственно получаем уравнение на собственные функции и собственные значения оператора импульса:
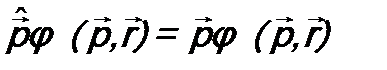 →
→ 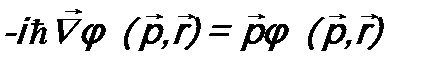 .
.
Его решение: спектр непрерывный, т.е.
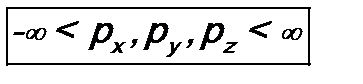 и
и 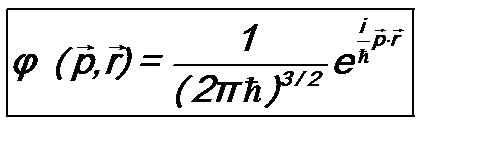 .
.
Лекция 15
СВОЙСТВА ПРОСТРАНСТВА-ВРЕМЕНИ
И ИНТЕГРАЛЫ СОСТОЯНИЯ КВАНТОВОЙ СИСТЕМЫ: МОМЕНТ ИМПУЛЬСА
 2020-04-12
2020-04-12 172
172








