2020-04-12
141
или моментом количества движения.
Из этого определения и коммутационного соотношения (15.2) следует, что оператор момента импульса системы микрочастиц должен быть пропорционален оператору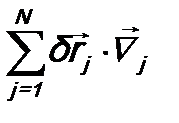 
. Выразим 
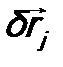через вектор 
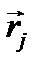и угол поворота δφ. Для этого сам поворот охарактеризуем вектором 
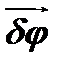, который перпендикулярен плоскости поворота и при этом 
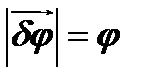. Тогда 
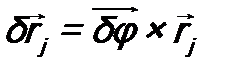((×) – знак векторного произведения). Далее для скалярного произведения получаем:
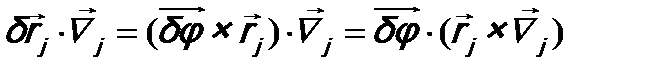. (15.3)
Здесь мы воспользовались свойством смешанного произведения трех векторов, позволяющим делать в нем их циклическую перестановку. Подставляя (15.3) в (15.2), вынося из под знака суммы и убирая вектор 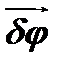, получим:
.
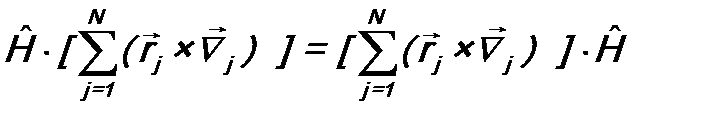В соответствии с данным выше определением оператором момента импульса системы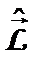 
следует назвать оператор
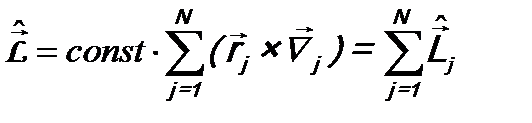, (15.4)
а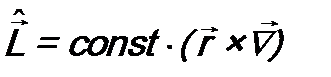 
- оператором момента импульса отдельной частицы. Из (15.4) видно, что оператор момента импульса системы 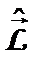аддитивен, а потому и сам момент импульса системы тоже будет обладать этим свойством, как и наблюдается. В операторе момента импульса частицы 
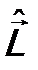можно положить: 
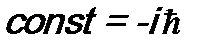. Тогда оператор 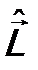примет уже известный нам вид: 
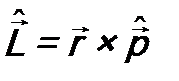, где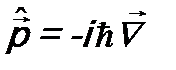 
- оператор импульса.
На практике обычно используются операторы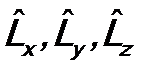 
и оператор квадрата момента импульса 
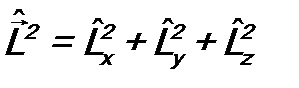. Операторы проекций момента импульса не коммутируют друг с другом:
.
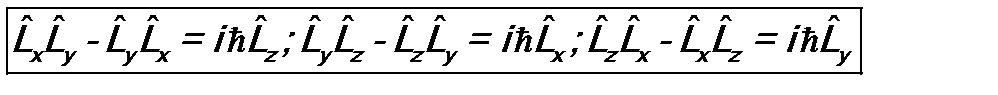Однако каждый из них коммутирует с оператором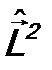 
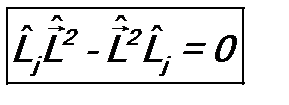, j = x, y, z.
Поскольку физически момент импульс характеризует повороты системы, на практике более удобным является его определение в сферической системе координат, где используются углы θ и φ. В этой системе координат операторы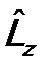 
и 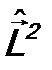имеют вид (см. также ф-лы (7.7)):
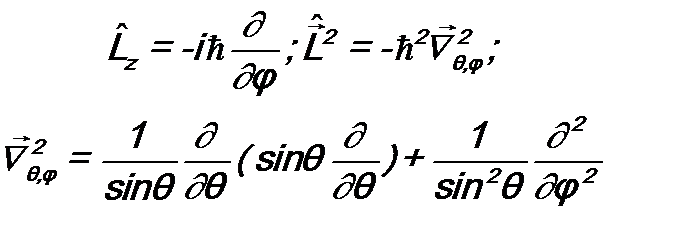. (15.5)
Используя операторы (15.5), можно найти их собственные функции и собственные значения. Получаем: для оператора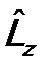
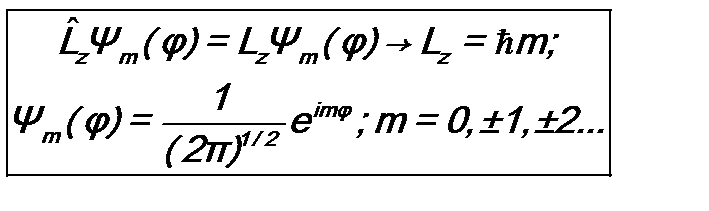; (15.6)
для оператора :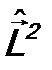
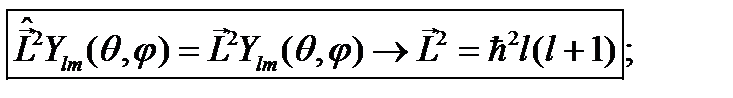(15.7)
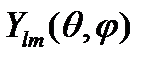- сферическая функция;
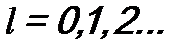- орбитальное квантовое число;
m = 0, ±1, ±2, …, ±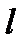 
- магнитное (иначе - азимутальное) квантовое число.
Из формул (15.5) и (15.6) видно, что для обоих операторов спектр дискретный, а для оператора 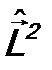он еще и вырожденный. Действительно, собственные значения 
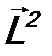зависят только от квантового числа 
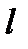, тогда как собственные функции 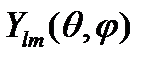еще и от квантового числа m, и кратность вырождения будет 
.
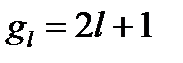Сферические функции 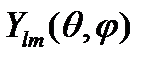хорошо известны в математической физике, они широко используются при решении задач квантовой механики. Их явный вид довольно сложен, и мы его приводить не будем. Однако, ввиду важности этих функций перечислим их главные свойства, которые позволяют их применять на практике.
1. Функции 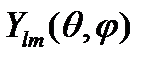- комплексные:
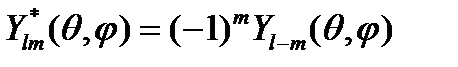. (15.8)
2. Они ортонормированы:
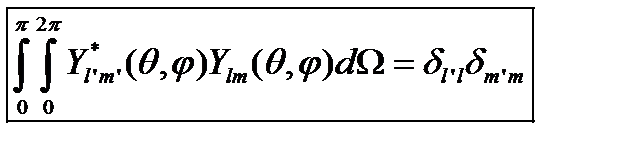. (15.9)
Здесь dΩ = sinθdθdφ – элемент телесного угла, δjk – символ Кронекера (см. (6.2)).
3. Обладают свойством полноты, т.е. произвольную функцию Ψ (θ, φ), удовлетворяющую стандартным условиям, можно по представить в виде разложения
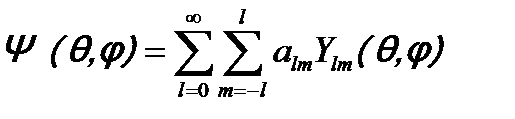, (15.10)
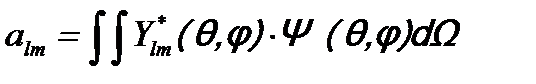. (15.11)
4. Мнимость сферической функции и ее зависимость от угла φ определяется только собственной функцией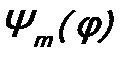 
оператора 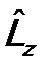, которую она содержит в виде сомножителя:
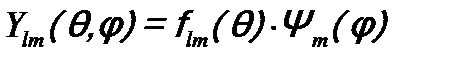, (15.12)
где функция от угла θ – действительная, т.е.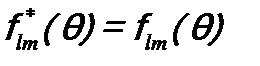 
. Как следствие соотношения (15.12), сферическая функция является собственной еще и для оператора :
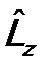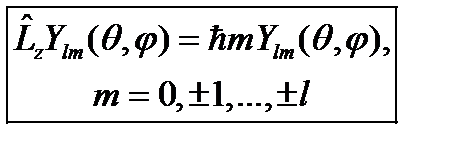. (15.13)
5. Приведем вид сферических функций низших порядков по индексу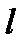 
, часто использующихся в приложениях:
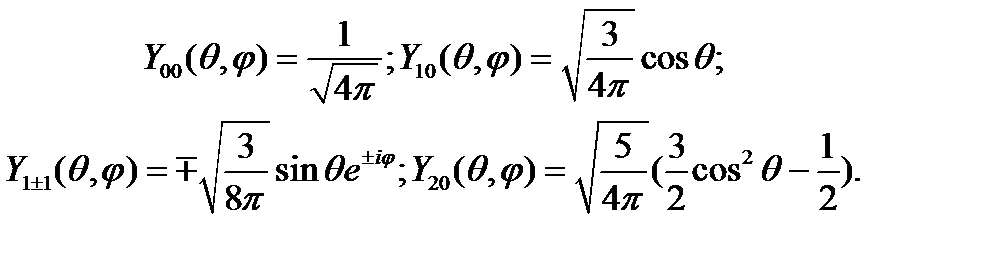
Лекция 16
СВОЙСТВА ПРОСТРАНСТВА-ВРЕМЕНИ
И ИНТЕГРАЛЫ СОСТОЯНИЯ: ЧЕТНОСТЬ
Предположим, что в пространстве имеется центр симметрии. Это означает, что состояние системы, состоящей из N частиц, не изменится при замене знака у координат всех частиц, т.е. при замене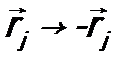 
(j = 0, 1, …, N). Операция такого рода называется инверсией, и можно ввести оператор инверсии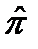 
: 
.
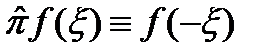Поскольку при наличии центра симметрии в пространстве состояние системы не изменяется, гамильтониан системы должен коммутировать с оператором инверсии:
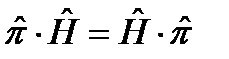. (16.1)
Из (16.1) следует, что должен быть некоторый интеграл состояния системы. В данном случае его называют четностью состояния. Выясним, что это означает.
Предположим, что решение уравнения Шредингера для стационарных состояний нам известно, в частности, известна волновая функция Ψ(ξ). Поскольку операторы 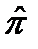и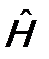 
коммутируют, у них должна быть общая система собственных функций (см. окончание лекции 5). Следовательно, волновая функция Ψ(ξ) будет собственной функцией и оператора инверсии :
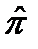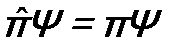, (16.2)
где 
- собственное значение. Подействуем на это уравнение оператором 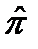еще раз и учтем, что двукратное действие этого оператора является тождественным преобразованием, т.е. 
.
.
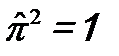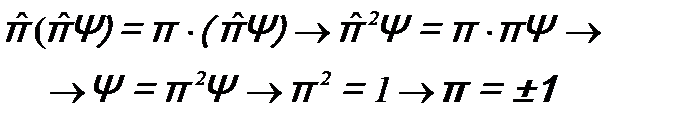В итоге: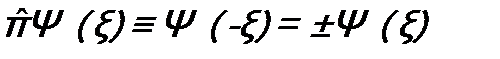 
.
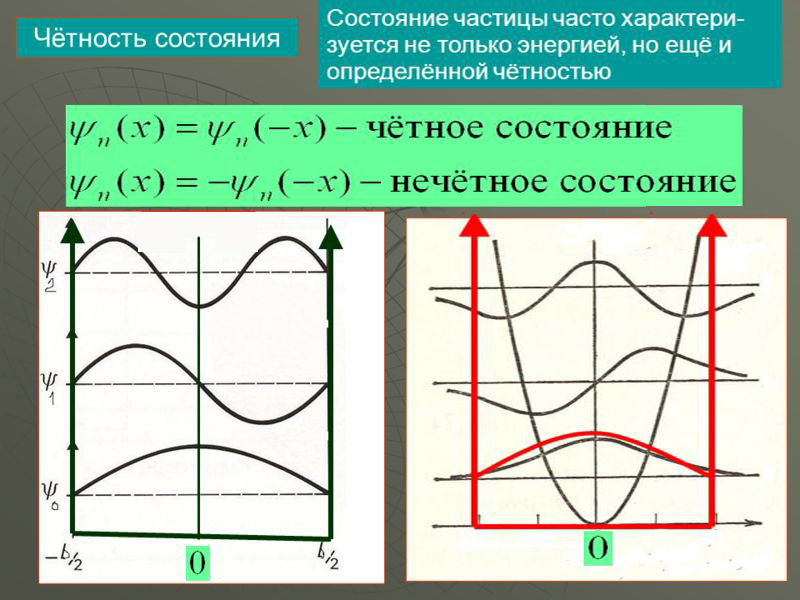
Это означает: когда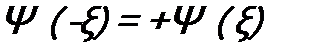 
, волновая функция четная, а когда 
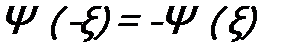- нечетная. Говорят, что волновая функция обладает определенной четностью и это ее свойство и будет интегралом состояния – четностью.
Пример 1. Квантовая система – одномерный гармонический осциллятор с массой m и частотой колебаний ω.
В этом случае гамильтониан имеет вид:
.
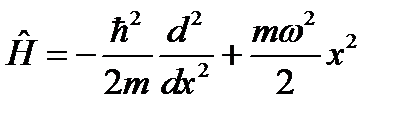Видно, что в точке 0 имеется центр симметрии, так как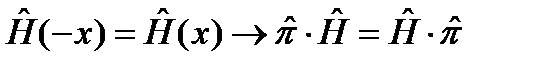 
. Следовательно, состояния такого осциллятора должны обладать определенной четностью. И действительно, можно показать, что решение уравнения Шредингера 
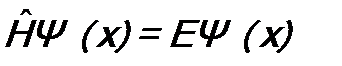дает волновые функции Ψn(x), зависящие от квантового числа n = 0, 1, 2, …, и оно будет определять четность состояний:
Ψn(-x) = (-1)n Ψn(x).
В итоге, состояния квантового осциллятора с четными значениями n = 0, 2, … будут четными, а с нечетными значениями n = 1, 3, … - нечетными.
Пример 2. Квантовая система – частица, движущаяся в поле центральных сил.
В этом случае потенциальная энергия частицы зависит только от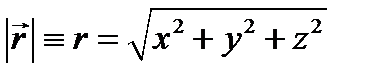 
. Гамильтониан в этом случае при замене 
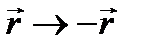изменяться не будет, и четность должна быть интегралом состояния. Можно показать, что в данной задаче в переменных (r, θ, φ) волновая функция имеет вид: 
,
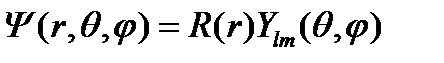где вид функции R(r) зависит от вида потенциальной энергии и находится из уравнения Шрёдингера, а 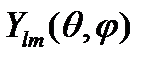- это уже известная нам сферическая функция с известными свойствами. При операции инверсии 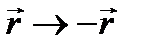в сферической системе координат 
:
.
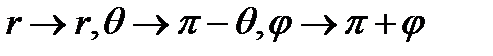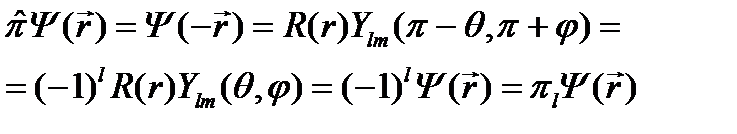Здесь собственное значение оператора четности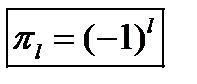 
и определяет четность состояний системы: для четных значений орбитального квантового числа 
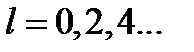состояния обладают положительной четностью, а для нечетных значений 
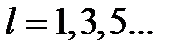- отрицательной.
