Изотропия пространства. Момент импульса

Изотропия (иначе – изотропность) пространства означает, что все направления в нем эквивалентны.

Слева – пространство изотропно, справа – анизотропно.

Если пространство обладает свойством изотропии, то поворот системы в нем на произвольный угол не меняет ее состояния. Состояние микросистемы определяется ее гамильтонианом 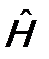, поэтому, как следствие, оператор поворота (обозначим его 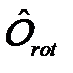) должен с ним коммутировать:

                     .                      (15.1)

Получим вид оператора 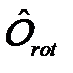. Пусть система состоит из N микрочастиц и каждая из них находится в точке с координатой 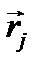(j = 1, 2, …, N). При повороте системы на некоторый угол δφ все координаты получат различные приращения 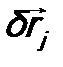(j = 1, 2, …, N), величина которых будет определяться углом δφ (при параллельном переносе величина приращения не зависела от j). В соответствии с этим, волновая функция системы будет преобразовываться следующим образом (как и раньше, принимаем, что 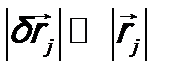, j = 1, 2, …, N):

,

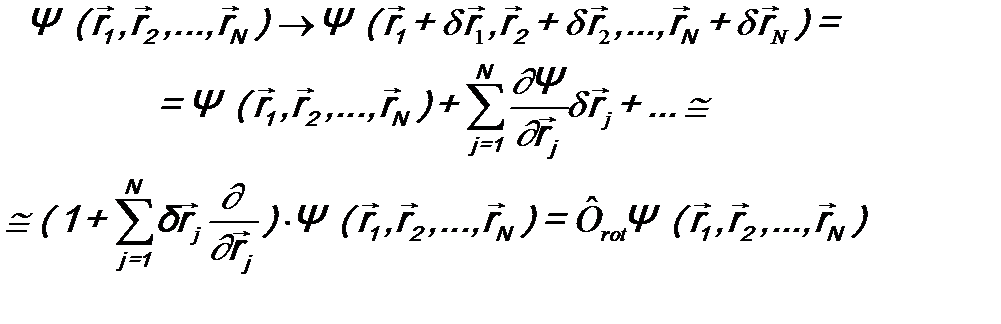где оператор 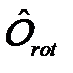 имеет вид:

.

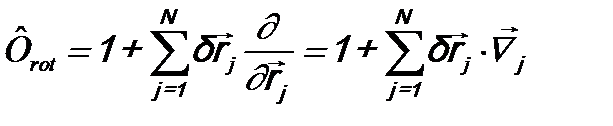Подставляя этот оператор в (15.1), получаем:

             .          (15.2)

Как известно, если некоторый оператор коммутирует с гамильтонианом, то должен быть соответствующий этому оператору интеграл состояния. Дадим определение: