2020-04-12
172
Предположим теперь, что имеется система частиц в силовом поле, имеющем центр симметрии, и частицы взаимодействуют друг с другом. В этом случае гамильтониан будет также включать слагаемое
, где 
- потенциальная энергия взаимодействия i -ой и j -ой частиц, 
- расстояние между ними (см. вид гамильтониана системы (9.9)). Возникает вопрос: останется ли гамильтониан симметричным и будет ли сохраняться четность? Для разных типов взаимодействия (электромагнитного, сильного и слабого) ответ был получен в 1956 г. физиками-теоретиками Т.Ли и Ч.Янгом совместно с физиком-экспериментатором Ц.Ву. Они проверили, что есть много экспериментальных свидетельств относительно электромагнитного и сильного взаимодействия: они четность сохраняют. Однако для слабого взаимодействия, из-за которого почти все наблюдаемые элементарные частицы и многие атомные ядра нестабильны и распадаются, таких доказательств не было. Совместно с Ц.Ву ими был поставлен эксперимент с бета-распадом ориентированных ядер изотопа кобальта-60 и показано, что слабое взаимодействие четность не сохраняет. Проявлялось это в асимметрии вылета бета-распадных электронов по направлению ориентации ядер и против нее.
Если бы четность сохранялась, вылет бета- электронов был бы симметричным.
За это открытие вышеперечисленные физики в 1957 году получили Нобелевскую премию по физике.
Что является удивительным в этом открытии? Операция инверсии с заменой 
- это замена декартовых переменных x, y, z на - x, -y, -z, что эквивалентно замене правой системы декартовых координат на левую (или наоборот). Физики привыкли, что физические законы – это объективная реальность, и они не зависят от того, в какой системе координат (правой или левой) их описывать. Результат должен был быть одинаков! Несохранение четности же означает, что описание явления в правой или левой системах координат даст различные результаты. Для явлений с участием слабого взаимодействия это было подтверждено экспериментально. Физика с такими явлениями столкнулась впервые. Заметим, что в классической физике такого интеграла состояния, как четность, не существует, это квантовое понятие.
Лекция 17
МАТРИЧНЫЙ ФОРМАЛИЗМ КВАНТОВОЙ МЕХАНИКИ – ТЕОРИЯ ПРЕДСТАВЛЕНИЙ
Основы матричного формализма в квантовой механике были заложены В.Гейзенбергом еще до того, как стало известным уравнение Шредингера. По своей сути, это ее альтернативный вариант, иногда более удобный при решении некоторых задач. В традиционном формализме волновая функция 
и собственные функции операторов определяются в координатном пространстве. В нем же действуют и физические операторы 
. В этом случае говорят о координатном представлении. Однако возможны и другие представления функций и операторов.
Пусть для некоторого линейного и эрмитового оператора 
известны собственные функции и собственные значения (для определенности пусть спектр будет дискретным):
(17.1)
Набор собственных функций { 
} – это основа для перехода к G -представлению. Оно называется так по оператору, чьи собственные функции используются.
Пусть волновая функция в координатном представлении известна: 
(время t не включаем). Пользуясь полнотой системы собственных функций оператора , разложим по ним волновую функцию:
. (17.2)
Соответственно для коэффициентов разложения имеем (см. (6.4)):
. (17.3)
Формулы (17.2) и (17.3) – это основа для перехода из координатного в G -представление и наоборот. Зная волновую функцию 
, по ф-ле (17.3) можно получить соответствующий ей набор коэффициентов { a1, a2, …, an, …}. И, наоборот, получив каким-то образом набор коэффициентов { a1, a2, …, an, …}, по ф-ле (17.2) можно найти волновую функцию . Иными словами, имеет место взаимно однозначное соответствие: 
{ a1, a2, …, an, …}. Оно позволяет назвать набор коэффициентов { a1, a2, …, an, …} тоже волновой функцией, но только не в координатном, а в G -представлении. Получается, что в G -представлении это не функция, а определенный набор чисел или матрица из этих чисел с одним столбцом:
. (17.4)
Пусть теперь оператор имеет непрерывный спектр и известны его собственные функции, т.е. решение уравнения
. (17.5)
Тогда вместо соотношений (17.2) и (17.3) будет
; (17.6)
. (17.7)
Как и в случае дискретного спектра имеет место взаимно однозначное соответствие волновой функции и функции a(G). Поэтому функцию a(G) можно назвать волновой функцией в
G -представлении.
Ограничимся дальше только случаем дискретного спектра у оператора . Рассмотрим, какой вид принимает заданный оператор 
. Пусть его действие определено соотношением:
, (17.8)
где от функций 
только требуется, чтобы они удовлетворяли стандартным условиям. Переведем их в G -представление.
; (17.9)
. (17.10)
В соответствии с данными выше определениями совокупности коэффициентов { a1, a2, …, an, …} и { b1, b2, …, bn, …} – это соответственно функции 
и 
в G -представлении. Подставляя разложения (17.9) и (17.10) в соотношение (17.8), получим его эквивалент в G -представлении.
.
Умножим обе части этого соотношения на 
, проинтегрируем по координате и воспользуемся свойством ортонормировки собственных
функций 
:
. (17.11)
Здесь, как и n, m = 1, 2, 3, … и введено обозначение
. (17.12)
Таким образом, соотношение (17.11) – это не одно, а система алгебраических уравнений, и она есть эквивалент соотношения (17.8) в G -представлении. Тогда входящую в эту систему уравнений матрицу из матричных элементов Fmn можно назвать оператором 
в G -представлении. Итак, получаем, что оператор в G -представлении имеет вид матрицы:
. (17.13)
Заметим, что систему уравнений (17.11) можно сразу записать в матричном виде:
.
Здесь (·) – символ матричного умножения, матрицы A и B – это функции и в G -представлении, имеющие вид
,
а матрица F была определена выше.
Посмотрим, как должен выглядеть оператор в своем собственном представлении, т.е. когда оператор - это и есть оператор : 
. Тогда функции - это собственные функции оператора :
(17.14)
Для матричных элементов Fmn в соответствии (17.12) получим:
.
Здесь использованы условие ортонормировки собственных функций и для подчеркнутого выражения соотношение (17.14). Таким образом, в своем собственном представлении оператор представляется диагональной матрицей и по диагонали стоят его собственные значения:
. (17.15)
Приведем еще часто используемый в матричном виде оператор 
, который называется оператором, сопряженным оператору , и часто используется на практике. В приведенном определении тильда означает транспонирование матрицы, т.е. замену строк на столбцы и наоборот, звездочка – операцию комплексного сопряжения.
.
Можно показать, что для эрмитово сопряженных операторов 
, т.е.
,
или 
(m, n = 1, 2, 3, …).
Пользуясь волновой функцией в G -представлении, можно рассчитать непосредственно в этом представлении среднее значение физической величины 
:
.
Таким образом, для вычисления среднего значения физической величины нет необходимости возвращаться из G -представления в координатное, можно сразу воспользоваться формулой
. (17.16)
Можно непосредственно в G -представлении найти собственные значения и собственные функции заданного оператора , т.е. эквивалент уравнения
. (17.17)
В G -представлении аналогичное уравнение будет иметь вид:
. (17.18)
Здесь матричные элементы Fmn определены ф-лой (17.12), cn - коэффициенты разложения искомой функции по базисным функциям, т.е. по собственным функциям оператора : 
. Их совокупность { c1, c2, …} для каждого собственного значения F будет определять искомую собственную функцию оператора в G -представлении.
Система уравнений (17.18) однородная. Как известно, для нахождения ее нетривиального решения (тривиальное – это все cn = 0) следует приравнять нулю определитель матрицы 
:
,
или в явном виде
.
Если определитель раскрыть, получится алгебраическое уравнение по степеням искомой величины F, решение которого даст его корни
F1, F2, …, Fk, … Подставляя k -ый корень Fk
в систему уравнений (17.18) и решая ее, найдем соответствующий набор коэффициентов 
, т.е. собственную функцию 
оператора в G -представлении. И так для каждого Fk (k = 1, 2, …), получив тем самым все соответствующие собственные функции в G -представлении.
Точно также непосредственно в G -представлении можно решить уравнение Шрёдингера для стационарных состояний, получить спектр энергий и соответствующие волновые функции. Вид уравнения Шрёдингера 
в G -представлении будет аналогичен алгебраической системе
уравнений (17.18):
(17.19).
Здесь набор коэффициентов { a1, a2, …} – волновая функция стационарного состояния в G -представлении и
(17.20)
- гамильтониан в G -представлении. Дальнейшие действия для нахождения энергетического спектра E1, E2,…, Ek,…и соответствующих волновых функций { 
} (k = 1, 2,…) из системы уравнений (17.19) такие же, как и при решении
системы уравнений (17.18).
Наконец, можно получить в G -представлении аналог временного уравнения Шрёдингера
; (17.21)
.
Перейдем в G -представлении, разложив волновую функцию 
по базисным функциям
(n = 1, 2, …):
. (17.22)
Подставляя (17.22) в (17.21) получим:
.
Умножим это равенство 
(m = 1, 2, …) и проинтегрируем по 
.
;
, m = 1, 2, … (17.23)
При получении (17.23) использовано условие ортонормировки для базисных функций и введено обозначение:
.
Это есть система дифференциальных уравнений первого порядка по времени. Ее решение позволяет найти совокупность величин a1(t), a2(t), …, an(t), …, т.е. волновую функцию в G -представлении. Однако для определенности решения необходимо к системе дифференциальных уравнений (17.23) задать начальные условия an(t=0) (n = 1, 2, …).
Суммируем все сказанное в виде таблицы.
|
| |
| Координатное представление | G -представление |
|
| { a1, a2, …, an, …} |
|  ;
|
|
|
|
|
|
|
|  ;
|
|
|  , m = 1, 2,…;
|
Лекция 18
СПИН ЭЛЕКТРОНА, СПИНОВЫЙ ФОРМАЛИЗМ
Электрон в атоме, двигаясь в кулоновском поле ядра, обладает орбитальным моментом. В этом поле в числе интегралов состояния электрона будут 
и 
: 
, где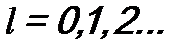 
- орбитальное квантовое число, и 
, всего 
значений. m – магнитное квантовое число. Это подтверждено экспериментально в опытах Штерна-Герлаха. В магнитном поле пучок атомов, находящихся в состоянии с 
, расщеплялся на пучок в соответствии с количеством значений магнитного квантового числа m. Однако было обнаружено, что и при 
, когда пучок не должен был расщепляться, так как m = 0, он все равно расщеплялся надвое.
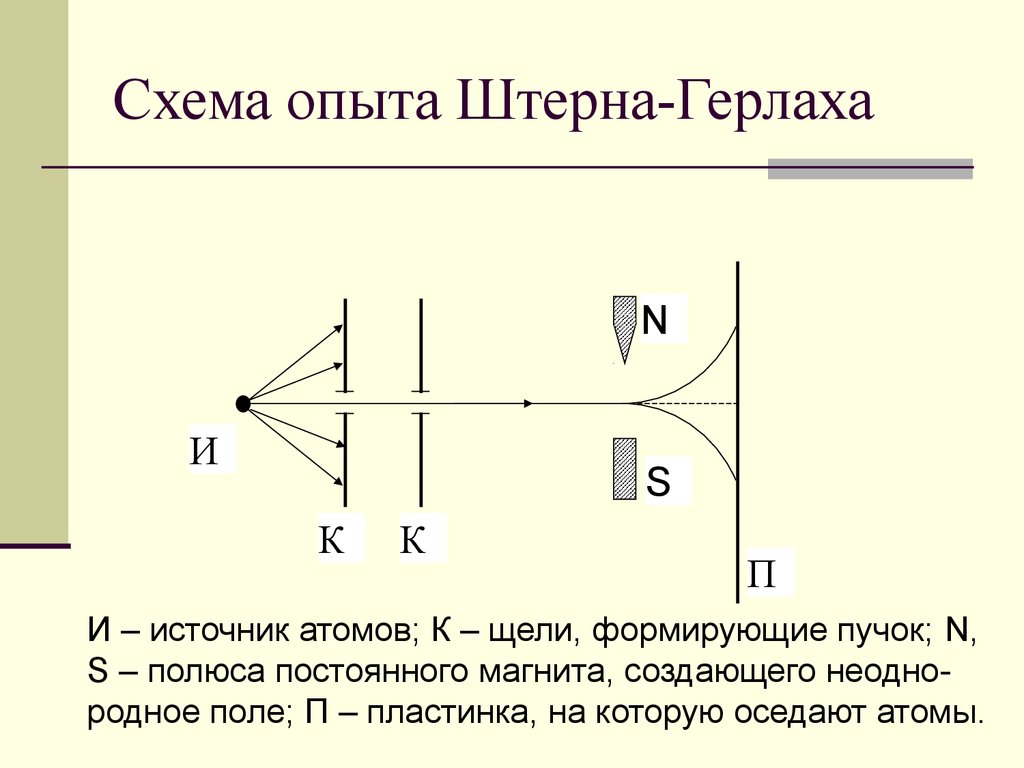
Для объяснения результата этого эксперимента было сделано предположение: электрон обладает собственным механическим моментом – спином 
. Его проекция sz на любое направление оси Оz может принимать только два значения: 
. Если по аналогии с ввести спиновое магнитное квантовое число ms, то тогда 
и 
. Также по аналогии с орбитальным квантовым числом 
можно ввести спиновое квантовое число s: 
(сравни с ). Однако, в отличие от квантового числа 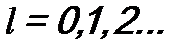, s принимает только одно значение: s = 1/2. Таким образом, есть аналогия 
, но со спецификой спина как собственного момента импульса: спиновое квантовое число принимает только одно значение s = 1/2, а спиновое магнитное квантовое число только два значения - 
. Спин нельзя понимать как вращение электрона вокруг собственной оси. Если бы это было так, то скорость вращения на его поверхности в 200 раз превышала бы скорость света. Спин электрона - это квантовое понятие, у него нет классического аналога. У электрона есть масса и электрический заряд, а теперь в квантовой механике еще и спин, и это тоже физическая характеристика.
В квантовой механике, если есть некая физическая величина, должен быть и соответствующий ей оператор. Следовательно, должен быть оператор спина 
. Его вид был введен в 1925 г. Дж.Уленбеком и С.Гаудсмитом, они же разработали и спиновый формализм.
Спин электрона – это тоже механический момент импульса. Поэтому постулируется, что для компонент оператора спина 
коммутационные соотношения такие же, как и для компонент оператора 
, т.е.
(18.1)
Еще, в соответствии с принципами квантовой механики, оператор спина должен быть эрмитовым:
. (18.2)
И все же спиновый формализм существенно отличается от формализма, связанного
с оператором . У проекции момента импульса 
различных значений , да и само орбитальное квантовое число 
может принимать любые целые значения от 0 до ∞. Проекция же спина , т.е. этих проекций всего две. Опираясь на этот факт, было предложено представлять спиновые операторы в виде матриц 2×2 и в дальнейшем использовать матричный формализм. Как известно, в своем собственном представлении матрица-оператор должна иметь диагональный вид, причем по диагонали должны стоять собственные значения (см. (17.15)). Поэтому каждая из матриц-операторов спина в своем собственном представлении должна иметь вид:
. (18.3)
Представим оператор спина в виде: 
. Здесь каждая из проекций 
имеют вид безразмерной матрицы 2×2, а в своем собственном представлении, в соответствии с (18.3), вид 
. Если возвести эту матрицу в квадрат, то получится:
, т.е. единичная матрица, или тождественное преобразование. Но единичная матрица остается такой в любом представлении. И это позволяет написать уже независимо от выбора представления, что
. (18.4)
Эрмитовость оператора спина позволяет для матричных операторов записать соотношения (см. (18.2)):
. (18.5)
Наконец, из коммутационных соотношений (18.1) с учетом определения получим:
(18.6)
Мы пока не знаем конкретного вида матричных операторов , но можно использовать соотношения (18.4)-(18.6) в качестве уравнений для нахождения матричных элементов этих операторов. Зададим представление – пусть это будет 
-представление. Тогда этот оператор в своем собственном представлении имеет вид диагональной матрицы: 
. Матрицы 
с не коммутируют, поэтому уже не будут диагональными:
,
и матричные элементы aij и bij надо найти. Подстановка матриц в соотношения (18.4)-(18.6) дает уравнения для нахождения чисел aij и bij, и этих уравнений достаточно для решения задачи. В итоге получаем:
. (18.7)
В этом виде эти матрицы называются матрицами Паули. Они дают вид операторов спина в соответствии с определением 
и записаны в -представлении. Хотя матрицы Паули – это операторы, «шляпку» над ними ставить не принято. Для матриц Паули можно получить полезные в приложениях два соотношения, которые являются следствием соотношений (18.6).
1). Матрицы Паули антикоммутируют:
.
2). 
.
Зная вид операторов спина в матричном представлении, можно найти и их собственные функции. Опять используем аналогию с моментом импульса. Как известно (см. (14.7) и (14.13)), его собственные функции удовлетворяют уравнениям:
; 
,
, 
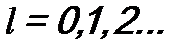. (18.8)
Пусть 
- собственная функция операторов 
и 
(аналог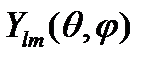 
). По аналогии с (18.8) она должна удовлетворять уравнениям:
, s = 1/2; (18.9)
, ms = ± 1/2. (18.10)
Первое уравнение не информативно. Действительно,
.
Здесь учтено свойство (18.4) операторов . Поскольку 
- это единичная матрица, действие оператора 
сводится к тождественному преобразованию, и уравнение (18.9) удовлетворяется любой функцией. Поэтому спиновую собственную функцию следует находить только из уравнения (18.10). Непосредственной подстановкой в уравнение (18.10) можно проверить, что эту функцию для значений ms= ± 1/2 можно взять в матричном виде:
. (18.11)
В этих определениях опущен индекс s = 1/2, так как он, в отличие от индекса 
у функции 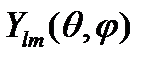, не меняется, принимая только одно значение. Такого рода двухкомпонентные функции называются спинорами.
Проверим, что, например, спиновая функция 
действительно удовлетворяет уравнению (18.10).
.
Из сравнения подчеркнутых членов с тем, что должно было получиться в соответствии с уравнением (18.10), следует, что функция в виде (18.11) и есть искомое решение. Отметим также, что, как и должно быть у собственных функций оператора, спиновые функции 
удовлетворяют условию ортонормировки:
. (18.12)
Проверим, например, нормировку спиновой функции 
и ортогональность спиновых функций и .
;
.
Рассмотрим теперь, как изменяется вид волновой функции, если в уравнении Шрёдингера учитывается наличие спина у микрочастицы. Для частицы со спиновым квантовым числом (часто говорят – со спином) s=1/2 и проекцией спина в волновую функцию следует включить еще и спиновую переменную sz, т.е. 
. Изучение свойств атомов показывает, что, в общем случае, имеет место корреляция орбитального движения электрона и направления спина. Она возникает из-за так называемого спин-орбитального взаимодействия, оператор которого имеет вид: 
и функция U задает силовое поле, в котором движется электрон. Поэтому волновые функции 
для 
и 
будут различаться. По сути, волновая функция тоже становится матрицей:
.
Однако в атомах спин-орбитальное взаимодействие по сравнению с полем ядра, также действующим на атомные электроны, гораздо слабее. Это позволяет в гамильтониане атома спин-орбитальным взаимодействием пренебречь, и он уже не будет зависеть от спиновых переменных электронов. Тогда становится возможным разделить переменные 
и sz в волновой функции и представить ее в виде: 
.
Здесь 
- решение уравнения Шрёдингера без учета спина у электрона, а зависимость от спиновых переменных войдет в решение через известную спиновую функцию .
Лекция 19
ЧАСТИЦА В ЭЛЕКТРОМАГНИТНОМ ПОЛЕ. УРАВНЕНИЕ ПАУЛИ
Пусть частица массы m еще имеет электрический заряд q и магнитный момент 
. Пусть также вместе с силовым полем 
на нее действует и электромагнитное поле. Как известно, его можно охарактеризовать или заданием напряженностей электрического и магнитного полей 
и 
, или скалярного и векторного потенциалов φ и 
.Эти два способа эквивалентны, так как имеют место соотношения:
(c – скорость света). В теории предпочитают использовать скалярный и векторный потенциалы, так как есть определенная свобода при их выборе. Обобщим уравнение Шрёдингера на случай, когда на частицу действует и электромагнитное поле.
Известно, как в такой ситуации в классической физике преобразуется функция Гамильтона: надо импульс частицы заменить на обобщенный и одновременно изменить силовое поле. Конкретно
(при необходимости всегда можно заменить на 
). В соответствии с постулатом 3 (см. лекцию 6) в гамильтониане 
следует сделать аналогичные замены:
. (19.1)
В (19.1) учтено, что в квантовой механике вместо магнитного момента может быть соответствующий оператор. Поскольку в общем случае и скалярный, и векторный потенциалы могут зависеть от времени, необходимо использовать временное уравнение Шрёдингера. В итоге, делая в нем замены (19.1), получим искомое уравнение:
. (19.2)
Можно записать гамильтониан в раскрытом виде. Для этого следует вычислить первый член с учетом того, что в общем случае оператор импульса 
и векторный потенциал 
не коммутируют. Вид их коммутатора известен (обычно задача его вычисления решается на практических занятиях):
. (19.3)
Часто для векторного потенциала используют калибровку 
и тогда 
, т.е. операторы коммутируют. Однако в общем случае необходимо использовать общее соотношение (19.3). С его учетом получаем:
. (19.4)
Подставляя (19.4) в (19.2), получим в раскрытом виде временное уравнение Шрёдингера для частицы в электромагнитном поле:
. (19.5)
Если положить φ=0 и 
, то 
,
где 
- гамильтониан для частицы, когда электромагнитное поле отсутствует.
Рассмотрим частный случай, когда частица – это электрон. Тогда m = me, q = -e и вид оператора магнитного момента для него тоже известен:
. (19.6)
Тогда временное уравнение Шрёдингера (19.2) принимает вид:
. (19.7)
Это есть уравнение Паули. Иными словами, уравнение Паули – это временное уравнение Шрёдингера для частицы в электромагнитном поле, только это конкретная частица – электрон.
Лекция 20
ДВИЖЕНИЕ ЧАСТИЦЫ В ЦЕНТРАЛЬНОМ ПОЛЕ – ОБЩИЕ СВОЙСТВА
Рассмотрим движение микрочастицы в поле, силовое воздействие которого на нее зависит от расстояния до центра силы, но не зависит от направления. Иными словами, потенциальная энергия частицы 
, или в сферических координатах r, θ, φ 
. Такое поле называется центральным.
С соответствующим гамильтонианом будут коммутировать операторы момента импульса ,
, так как они действуют только на угловые переменные, и инверсии, т.е.
. (20.1)
Как следствие, интегралами движения у такой частицы будут энергия E (гамильтониан сам с собой тоже коммутирует), квадрат момента импульса (орбитальное квантовое число 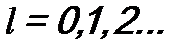), компонента момента импульса 
(магнитное квантовое число 
) и четность 
(см. пример 2 в лекции 15). Волновая функция будет находиться из уравнения Шрёдингера. Как известно (см. свойство 1 в лекции 6), если операторы коммутируют, то у них должна быть общая система собственных функций.
Вследствие (20.1) волновая функция частицы в центральном поле должна одновременно удовлетворять уравнениям:
; (20.2)
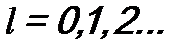, ; (20.3)
; (20.4)
. (20.5)
Потенциальная энергия частицы в центральном поле не зависит от угловых переменных, поэтому удобно искать решение уравнений (20.2)-(20.5) в сферической системе координат, т.е. 
. Как известно (см. (15.7) и (15.13)), решением уравнений (20.3) и (20.4) является сферическая функция 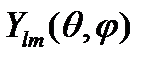. Она же удовлетворяет и уравнению (20.5), как это было показано в примере 2 в лекции 15. Следовательно, при решении уравнения Шрёдингера (20.2) волновую функцию можно искать в виде:
. (20.6)
Такой вид волновой функции позволит одновременно удовлетворить уравнениям (20.3)-(20.5), а также отделить угловые переменные в уравнении (20.2). Для этого надо уравнение Шрёдингера (20.2) записать в сферических переменных, используя соответствующий вид гамильтониана (см. (7.13)):
. Подставим сюда волновую функцию в виде (20.6) и учтем действие на нее оператора (20.3). Сократив после этого сферическую функцию, получим радиальное уравнение:
.
Это уравнение можно упростить, используя стандартную замену искомой радиальной функции:
. (20.7)
Легко проверить, что
. (20.8)
Подставляя (20.7) в радиальное уравнение и учитывая (20.8), окончательно получим:
. (20.9)
Как видно, это одномерное уравнение по переменной r. С заменой R →Ψ и r → x оно совпадало бы с одномерным уравнением Шрёдингера для стационарных состояний
,
только теперь к потенциальной энергии добавлен центробежный член 
.
Для дальнейшего решения уравнения (20.9) необходимо конкретизировать вид потенциальной энергии 
. Сделаем два предположения.
1. 
, если r → ∞.
Действительно, известные в физике силы при действии на частицу стремятся к нулю с ростом расстояния от силового центра. Но, как известно, сила 
. Поэтому, если при r → ∞ потенциальная энергия 
, то сила будет исчезать. Величину же константы всегда можно положить равной нулю, и этот ноль в дальнейшем можно считать началом отсчета энергии частицы.
2. 
, если r → 0; α < 2.
A – это константа, которая может быть и положительной, и отрицательной.
Исследование уравнения (20.9) показывает, что оно может иметь сингулярность в точке r = 0, но при этом должно быть α < 2. Если будет α ≥ 2 и при этом A < 0 (это притяжение частицы к центру силы), то частица обязательно упадет на центр. Такую ситуацию указанное требование к параметру α исключает. Итак,
(20.10)
Исследуем асимптотическое поведение решения уравнения (20.9).
1. Пусть r → ∞. Тогда и центробежный член → 0. Уравнение (20.9) принимает вид:
, или
. (20.11)
Это уравнение однородное и его решение можно искать в виде 
. Подставляя его в (20.9), получаем характеристическое уравнение для нахождения параметра λ:
.
Соответственно общее решение 
имеет вид:
, (20.12)
где C 1 и C 2 - произвольные константы. Далее можно рассмотреть два случая: E>0 и E<0.
а). Пусть E>0. Тогда и k 2 >0, т.е. k – действительная величина. Следовательно, для этого случая решение уравнения (20.11) можно взять непосредственно в виде (20.12). Полная же радиальная функция будет иметь вид:
, (20.13)
и это решение общее. Оно удовлетворяет стандартным условиям при любом выборе констант C 1 и C 2.
Можно найти вероятность dW обнаружения частицы в слое между сферами с радиусами
r и r+dr:
.
Здесь плотность вероятности
,
и она остается конечной для частицы на любом ее расстоянии r от силового центра. Иными словами, если энергия частицы E>0, она может уйти как угодно далеко от силового центра. Движение такого рода называется апериодическим, или инфинитным.
б). Пусть E<0. Тогда и k 2 <0, т.е. k – мнимая величина. Положим 
, где 
- действительная величина. Тогда для данного случая общее решение (20.13) принимает вид:
. (20.14)
При r → ∞ последнее слагаемое стремится к бесконечности и функция 
не удовлетворяет требованию конечности. Следовательно, вместо общего решения (20.14) надо взять частное, положив константу 
= 0. В результате
, (20.15)
и это решение частное. Используя решение (20.15), можно опять определить вероятность dW найти частицу в слое между сферами радиусов
r и r+dr:
,
где в данном случае плотность вероятности
, если r → ∞. Иными словами, в отличие от предыдущего случая, частица не может уйти далеко от силового центра, а будет двигаться около него. Потому при E<0 движение частицы называется периодическим, или финитным.
2. Пусть r → 0. Тогда с учетом поведения потенциальной энергии в виде (20.10) уравнение (20.9) принимает вид:
, (20.16)
и все члены в нем существенны. Так как в рассматриваемом пределе интерес представляют малые величины радиальной переменной, решение можно искать в виде
ряда по степеням r:
. (20.17)
Обращаем внимание, что в разложении (20.17) ряд начинается не с нулевой степени r, а с rγ. Величину γ требуется найти из условия, чтобы в уравнении (20.16) не было расходящихся членов при r → 0. Они могут возникнуть в (20.16) из-за наличия справа в знаменателях двух последних членов переменной r. Если подставить функцию 
в виде (20.17) и найти условие, при выполнении которого старший член (с наименьшей степенью) получившегося ряда обратится в ноль (остальные члены ряда имеют большие степени и при r → 0 сами станут нулевыми), то можно определить величину γ.
В итоге 
или 
и этот результат
не зависит от знака энергии E. Соответственно общее решение уравнения (20.16) имеет вид:
.
При r → 0 второе слагаемое расходится, и решение не будет удовлетворять требованию конечности. Следовательно, вместо общего решения надо взять частное, положив 
.
Таким образом, получаем
и, соответственно,
. (20.18)
Обращаем внимание еще раз, что это решение частное, и оно справедливо как для E>0, так и для E<0.
Подведем итог. Предположим, что нам было бы известно точное решение 
исходного уравнения (20.9). Тогда оно должно было бы обладать следующей асимптотикой:
.
Допустим, что мы двигаемся по координате r от нуля до бесконечности. При E>0 частное решение в виде (20.18) должно переходить в общее решение (20.13). Поскольку решение (20.13) общее, такой переход при любом значении энергии E (а это единственный параметр в исходном уравнении, который нам пока не известен) всегда осуществим. Иными словами, всегда в общем решении найдутся какие-то конкретные значения констант С1 и С2, и это решение останется конечным. Это означает, что при E>0 энергия у частицы может быть любая, т.е. ее спектр энергий будет непрерывным.
Другая ситуация будет при E<0, когда частное решение (20.18) должно переходить опять-таки в частное решение (20.15). В этом случае требуется уже определенный выбор констант в решениях, а это будет возможно не при любых, а только при конкретных значениях энергии E у частицы. Это означает, что при E<0 ее спектр энергий будет дискретным: E = E1, E2, …, En, …
Пример: кулоновское поле точечного ядра в атоме водорода. В этом случае потенциальная энергия электрона имеет вид: 
. У переменной r в знаменателе показатель степени α =1, т.е. α < 2, и условие (20.10) выполнено. Кривая на рисунке показывает ход зависимости потенциальной энергии от r. На нем также показан спектр энергий электрона. При
E < U(∞)=0 он дискретный – это связанные состояния электрона в атоме водорода. При
E > U(∞)=0 спектр непрерывный и физически это соответствует отрыву электрону от ядра, т.е. случаю ионизации атома водорода.
Суммируем полученные результаты.
1. В центральном поле у частицы интегралами состояния будут энергия E, квадрат момента импульса (орбитальное квантовое число 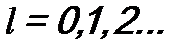), проекция момента импульса (магнитное квантовое число ) и четность .
2. Угловые переменные в уравнении Шрёдингера отделяются, если волновая функция ищется в виде:
,
где 
- известная сферическая функция.
3. Уравнение для нахождения радиальной функции 
имеет вид одномерного уравнения Шрёдингера при формальной замене в нем координаты x на переменную r
и потенциальной энергии
(добавляется центробежный член).
4. При E>0 энергетический спектр непрерывный и движение частицы апериодическое (инфинитное). При E<0 энергет
