Рассмотрим неоднородную линейную систему 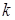 уравнений с
уравнений с 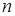 неизвестными
неизвестными
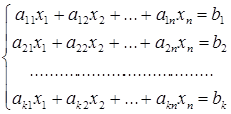 (3)
(3)
и сформулируем условия её совместности. Дописывая к основной матрице 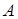 столбец
столбец 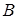 из свободных членов, получим расширенную матрицу
из свободных членов, получим расширенную матрицу
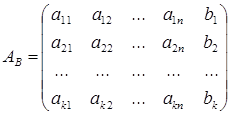 .
.
В теории линейных систем важнейшую роль играет
Теорема (критерий Кронекера-Капелли). Система (3) совместна тогда и только тогда, когда ранг её расширенной матрицы равен рангу основной матрицы:
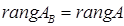 .
.
Доказательство.
Необходимость. Пусть система (3) совместна, т.е. существует набор чисел 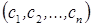 такой, что имеют место равенства
такой, что имеют место равенства
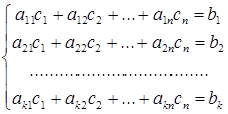 (4)
(4)
На языке столбцов равенства (4) записываются так:
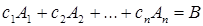 . (5)
. (5)
Рассмотрим линейную оболочку 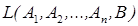 , порождённую столбцами расширенной матрицы. В силу равенства (5) столбец
, порождённую столбцами расширенной матрицы. В силу равенства (5) столбец 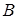 линейно зависит от столбцов
линейно зависит от столбцов 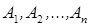 , поэтому (одно из свойств линейной оболочки) это столбец можно исключить из оболочки, не изменяя её:
, поэтому (одно из свойств линейной оболочки) это столбец можно исключить из оболочки, не изменяя её:
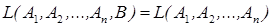 .
.
Но тогда
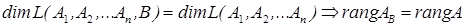 .
.
Достаточность. Пусть 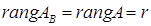 . Рассмотрим
. Рассмотрим 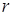 базисных столбцов матрицы
базисных столбцов матрицы 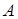 , они являются базисными и для расширенной матрицы
, они являются базисными и для расширенной матрицы 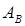 . По теореме о базисном миноре последний столбец матрицы
. По теореме о базисном миноре последний столбец матрицы 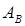 , т.е. столбец
, т.е. столбец 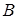 , может быть представлен в виде линейной комбинации её базисных столбцов. Добавляя к такой комбинации все небазисные столбцы матрицы
, может быть представлен в виде линейной комбинации её базисных столбцов. Добавляя к такой комбинации все небазисные столбцы матрицы 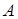 (например, с нулевыми коэффициентами), получаем, что существуют числа
(например, с нулевыми коэффициентами), получаем, что существуют числа 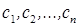 такие, что справедливо равенство (5). А это и означает, что
такие, что справедливо равенство (5). А это и означает, что 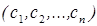 - решение системы (3), т.е. система совместна.¨
- решение системы (3), т.е. система совместна.¨
Пример 2. Рассмотреть с точки зрения критерия Кронекера-Капелли очевидно несовместную систему 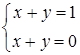 (пример из п. 1).
(пример из п. 1).
Решение. Для этой системы
основная матрица 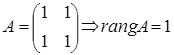 ,
,
расширенная матрица 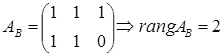 .
.
Здесь 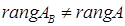 - условие теоремы не выполнено, система несовместна.¨
- условие теоремы не выполнено, система несовместна.¨
Пример 3. Выяснить, когда три прямые
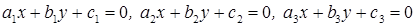
проходят через одну точку.
Решение. Переведём геометрическую задачу на язык линейных систем: при каком условии совместна система трёх линейных уравнений с двумя неизвестными
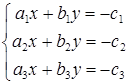 .
.
Критерий Кронекера-Капелли даёт такое условие:
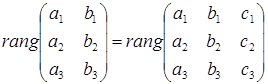 .¨
.¨
Пример 4. Пусть 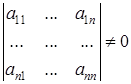 . Рассмотрим систему
. Рассмотрим систему
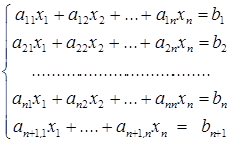 (*)
(*)
Здесь 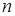 неизвестных и
неизвестных и 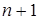 уравнение.
уравнение.
Докажите самостоятельно следующее утверждение: система (*) совместна тогда и только тогда, когда
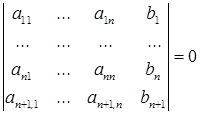 .¨
.¨
Пример 5. Сформулируйте критерий Кронекера-Капелли для квадратных систем и сопоставьте с теоремой Крамера.¨
ЛЕКЦИЯ 8
 2020-04-12
2020-04-12 194
194








