Нетривиальная совместность линейной однородной системы

Новое определение ранга матрицы

Рассмотрим матрицу

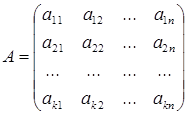.                                         (1)

Столбцы 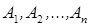 этой матрицы - элементы 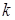-мерного координатного пространства 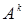. Пусть  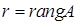и пусть для определённости первые  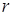столбцов матрицы  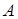являются базисными. Тогда по теореме о базисном миноре столбцы  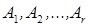линейно независимы и любой столбец матрицы  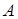представим в виде их линейной комбинации. Все столбцы  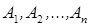порождают линейную оболочку 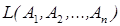. Размерность этой оболочки - максимальное число линейно независимых столбцов - равна 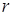. Получаем

.

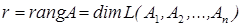Значит, ранг матрицы можно определить как максимальное количество её линейно независимых столбцов.

       Транспонируем матрицу 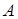, т.е. перейдём к матрице 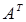, строки которой являются столбцами матрицы 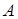. При этом ранг матрицы как наивысший порядок её отличного от нуля минора не изменится: 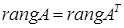. С другой стороны, по новому определению ранг матрицы  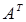равен максимальному количеству её линейно независимых столбцов или, что то же самое, максимальному количеству линейно независимых строк матрицы 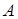. Приходим к несколько неожиданному заключению: максимальное количество линейно независимых столбцов любой матрицы совпадает с максимальным количеством её линейно независимых строк.

Нетривиальная совместность линейной однородной системы

       Рассмотрим однородную систему линейных уравнений с матрицей (1)

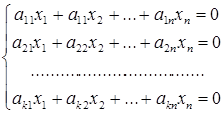                                 (2)

Мы уже отмечали, что такая система всегда совместна, так как обладает тривиальным решением 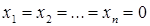. Основная задача, с которой приходится встречаться при изучении линейных однородных систем, состоит в выяснении условия, гарантирующего нетривиальную совместность системы, то есть наличие отличных от нуля решений. Такое условие даёт

Теорема (критерий нетривиальной совместности однородной системы). Однородная система линейных уравнений нетривиально совместна тогда и только тогда, когда ранг матрицы меньше числа неизвестных: .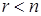

Для доказательства запишем систему (2) на языке столбцов:

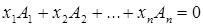
Вспомним (см. пр. 2 п.14), что существование ненулевого решения системы (2) равносильно линейной зависимости системы векторов 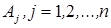. Но линейная зависимость столбцов матрицы имеет место тогда и только тогда, когда не все они являются базисными, т.е. когда .¨

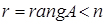       Заметим: если в системе (2) 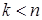 (число уравнений меньше числа неизвестных), то 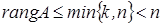, поэтому нетривиальные решения у такой системы всегда существуют.

       Следствие. Для того, чтобы квадратная однородная система линейных уравнений была нетривиально совместной, необходимо и достаточно, чтобы .

       В самом деле, при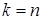

.¨

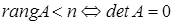       Напомним, что квадратная однородная система, у которой 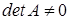, в силу теоремы Крамера имеет единственное решение - тривиальное. Таким образом, для квадратных однородных систем  ответ на вопрос о наличии ненулевых решений зависит от определителя матрицы 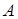: если  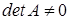(т.е. ), то тривиальное решение является единственным, если  (т.е. 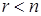), то система нетривиально совместна.

       Пример 1. Пусть в системе (2) 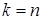 и . Убедиться, что совокупность 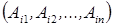 алгебраических дополнений элементов 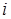-ой строки матрицы  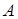есть решение системы.

Решение. Действительно, подставляя в 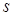-ое уравнение системы (2)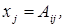 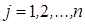, получим сумму

,

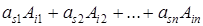которая при 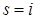 даёт , т.е. равна нулю по условию, а при 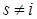 равна нулю как сумма произведений элементов 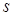-ой строки определителя  на алгебраические дополнения «чужой» 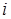-ой строки. Если отличен от нуля хотя бы один из миноров 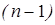-ого порядка (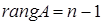), то предложенное решение является нетривиальным.¨