2020-04-12
111
Теорема Кронекера-Капелли устанавливает критерий совместности произвольной линейной системы, но не даёт способа решения этой системы. Приведём алгоритм отыскания всех решений системы (3).
(3)
Пусть система (3) совместна, 
и базисный минор 
расположен в левом верхнем углу матрицы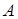 
(этого всегда можно добиться некоторой перестановкой уравнений и изменением нумерации неизвестных в системе). Тогда первые 
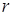строк являются базисными как для основной, так и для расширенной матрицы, а каждая следующая строка, начиная с 
-ой, есть линейная комбинация первых 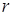строк. Переведём на язык систем: начиная с -ого, каждое уравнение системы (3) является следствием первых 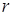уравнений. Поэтому система (3) 
уравнений равносильна системе первых 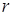уравнений:
(6)
В левой части системы (6) оставлены 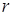основных неизвестных 
; 
свободных неизвестных 
перенесены в правую часть. Если свободным неизвестным придать произвольные значения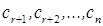 
, то система (6) превращается в систему 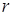уравнений с 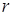неизвестными, причём её определитель 
. Единственное решение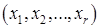 
этой системы определяется формулами Крамера:
|
|
|
(7)
Здесь дописана вторая строка - значения 
свободных неизвестных . Выражение в фигурных скобках получено с учётом линейного свойства определителя. Соотношения (7) свидетельствуют, что существует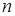 
чисел, которые при подстановке в систему (6) вместо неизвестных 
обращают все уравнения в тождества. Эта совокупность чисел является решением и равносильной системы (3).
Первая строка формул (7) определяет 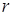основных неизвестных 
через коэффициенты системы 
, правые части 
и произвольные величины 
. Вместе обе строки формул (7) дают общее решение системы (3).
Действительно, во-первых, при любом выборе свободных неизвестных 
по формулам Крамера однозначно определяются основные неизвестные 
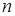, тогда совокупность чисел (
, 
) есть решение системы (3);
во-вторых, любое решение (, 
) системы (3) содержится в формулах (7) при соответствующем выборе свободных неизвестных, а именно, при 
.
Решение (, 
), полученное из общего решения (7) при фиксированных значениях произвольных постоянных, называется частным решением системы (3).
Замечание. Если у совместной системы (3) ранг 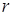матрицы равен числу 
неизвестных, то 
и свободные неизвестные отсутствуют. Соотношения (7) перейдут в знакомые формулы 
, определяющие единственное решение системы. Значит, система (3) является определённой при условии 
и неопределённой, если 
.
Пример 6. Найти все решения линейной системы
(8)
|
|
|
Решение. Прежде всего, выясним, совместна ли эта система. Выпишем расширенную матрицу, отделяя чертой столбец из правых частей. При помощи элементарных преобразований приведём эту матрицу к ступенчатому виду (метод Гаусса). Обращаем внимание на то, что будем работать только со строками матрицы или - на языке систем - только с уравнениями, переходя всякий раз к равносильной системе.
~
~ 
система совместна.
Так как количество неизвестных 
, то имеется 
свободных неизвестных, т.е. система неопределена. Если в качестве базисного взять минор 
, то неизвестные 
- основные, а неизвестные 
- свободные.
Придадим свободным неизвестным произвольные значения 
и в соответствии с оставшимися двумя строками матрицы запишем крамеровскую систему, равносильную заданной системе (8):
. (9)
Единственное решение этой системы проще всего получить, вычитая второе уравнение из первого:
.
Дописывая к найденным основным неизвестным свободные, получим совокупность пяти чисел
, (10)
которая и представляет собой общее решение системы (9) - и равносильной системы (8). Полагая, например, 
, получим частное решение 
, полагая 
, получим другое частное решение 
.¨
