Пространство геометрических векторов,
1о. Направленные отрезки.
Рассмотрим в пространстве две точки А и В. Они определяют отрезок АВ.
Определение 1. Отрезок АВ называется направленным, если его концы А и В упорядочены; если при этом первой является точка А, а второй – точка В, то А – начало отрезка, а В – его конец.
Направленный отрезок обозначается AB (а также 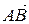 или
или 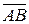 ). На чертеже направленный отрезок снабжен стрелкой на конце(см. рис.1)
). На чертеже направленный отрезок снабжен стрелкой на конце(см. рис.1)
Определение 2. Длиной 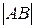 направленного отрезка
направленного отрезка 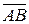 называется длина отрезка АВ.
называется длина отрезка АВ.
 |
Рис.1. Направленный отрезок АВ.
Определение 3. Направленные отрезки 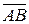 и
и 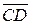 называются сонаправленными (обозначается
называются сонаправленными (обозначается 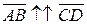 ), если они лежат на параллельных прямых и направлены в одну сторону.
), если они лежат на параллельных прямых и направлены в одну сторону.
Направленные отрезки 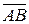 и
и 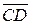 называют противоположно направленными (пишут
называют противоположно направленными (пишут 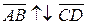 ), если они лежат на параллельных прямых и направлены в разные стороны.
), если они лежат на параллельных прямых и направлены в разные стороны.
Направленные отрезки 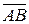 и
и 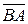 называются противоположными.
называются противоположными.
Каждую точку А пространства можно рассматривать как направленный отрезок с совпадающим началом и концом. Этот отрезок обозначается 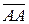 и называется нулевым направленным отрезком. Его длина считается равной нулю, а направление не определено.
и называется нулевым направленным отрезком. Его длина считается равной нулю, а направление не определено.
Определение 4. Два направленных отрезка 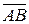 и
и 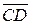 считаются эквивалентными, если они сонаправлены и имеют равные длины. (Обозначают
считаются эквивалентными, если они сонаправлены и имеют равные длины. (Обозначают 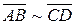 ).
).
Эквивалентность является отношением эквивалентности в множестве всех направленных отрезков, т.к. из определения эквивалентности следует:
1) отрезок 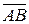 эквивалентен сам себе;
эквивалентен сам себе;
2) если 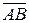 эквивалентен
эквивалентен 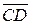 , то
, то 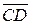 эквивалентен
эквивалентен 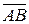 ;
;
3) если 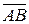 эквивалентен
эквивалентен 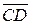 и
и 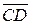 эквивалентен
эквивалентен 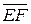 , то
, то 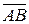 эквивалентен
эквивалентен 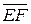 .
.
Так как эквивалентность направленных отрезков является отношением эквивалентности, то множество всех направленных отрезков пространства разбивается на непересекающиеся классы – классы эквивалентности. Классы эквивалентности образуют фактор-множество множества всех направленных отрезков пространства.
Определение 5. Множество всех эквивалентных направленных отрезков называется вектором (или свободным вектором).
Замечание. Напомним, что в средней школе вектор характеризует параллельный перенос.
Направление эквивалентных направленных отрезков называется направлением вектора, а их длина – длиной вектора.
Таким образом, любой направленный отрезок однозначно определяет вектор, а вектор – это класс эквивалентных направленных отрезков.
Поэтому часто пишут вектор 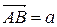 ,
, 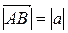 .
.
Определение 6. Вектор a такой, что 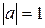 называется единичным вектором или ортом. Множество нулевых отрезков называется нулевым вектором
называется единичным вектором или ортом. Множество нулевых отрезков называется нулевым вектором 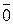 ; Его длина равна нулю, а направление не определено.
; Его длина равна нулю, а направление не определено.
Определение 7. Два ненулевых вектора, направления которых совпадают или противоположны, называются коллинеарными. Обозначают 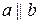 .
.
Нулевой вектор считается коллинеарным любому вектору.
Очевидно, что прямые, на которых лежат представители классов коллинеарных векторов, параллельны.
Определение 8. Три и более векторов называются компланарными, если они параллельны некоторой плоскости.
Для определенности любую тройку векторов, содержащую нулевой вектор, считают компланарной.
Пусть даны два вектора a и b. Из произвольной точки O пространства отложим 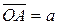 и
и 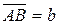 . Тогда
. Тогда 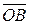 есть направленный отрезок и значит, определяет вектор.
есть направленный отрезок и значит, определяет вектор.
Покажем, что введенная операция сложения векторов корректно определена, т.е. вектор 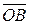 не зависит от выбора точки O. Для этого выберем другую точку
не зависит от выбора точки O. Для этого выберем другую точку 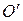 . Пусть
. Пусть 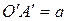 ,
, 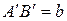 . Тогда
. Тогда 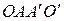 – параллелограмм; аналогично,
– параллелограмм; аналогично, 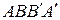 – параллелограмм
– параллелограмм 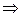
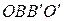 – параллелограмм
– параллелограмм 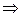
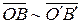 , то есть они определяют один и тот же вектор.
, то есть они определяют один и тот же вектор.
Определение 9. Вектор 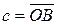 называется суммой векторов
называется суммой векторов 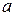 и
и 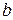 . Пишут:
. Пишут: 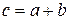 .
.
Способ сложения векторов, изложенный выше, называется правилом треугольника. Можно также использовать правило параллелограмма.
 2015-06-28
2015-06-28 2227
2227