2015-05-05
375
Система векторов e 1, e 2, …, en Î V называется базисом пространства V, если эта система векторов линейно независима и полна в V.
17°. Минимальный полный в V набор векторов является базисом.
◀ Докажем линейную независимость e 1, e 2, …, en.
Если они линейно зависимы, то, по крайней мере, один из векторов может быть записан как линейная комбинация остальных: en = a1 e 1 + a2 e 2 +…+ a n –1 en –1, следовательно, e 1, e 2, …, en – 1, полный набор, что противоречит минимальности исходного набора. ▶
18°. Максимальный линейно независимый в V набор является базисом.
◀ Докажем полноту набора e 1, e 2, …, en. Допустим, набор не полон. Тогда $ x Î V который не выражается как линейная комбинация e 1, e 2, …, en, тогда система x, e 1, e 2, …, en линейно независима, что противоречит максимальности исходного набора. ▶
19°. Всякое линейное пространство (кроме V º {q}) имеет базис.
◀ Доказательство можно провести построением: а) минимального полного набора или б) максимального линейно независимого набора. ▶
20°. Все базисы линейного пространства содержат одно и то же количество векторов.
|
|
|
◀ Пусть в пространстве V имеется два базиса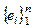 
и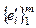 
:
1) 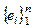– полный, а 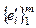– линейно независимый, тогда m ≤ n (т. 16°);
2) 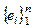– линейно независимый, а 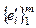– полный, тогда n ≤ m (т. 16°) Получаем m = n. ▶
Количество векторов в базисе называется размерностью пространства V и обозначается dim V.
21°. Чтобы линейно независимая система векторов была базисом необходимо и достаточно, чтобы количество векторов в этой системе равнялось размерности пространства
n = dim V. Доказать самостоятельно.
22°. Чтобы полная система векторов была базисом, необходимо и достаточно, чтобы количество векторов в этой системе равнялось размерности пространства n = dim V.
Доказать самостоятельно.
