I. Решение простейших тригонометрических уравнений.
| Уравнение | Формулы решения | Частные случаи |
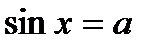
| при 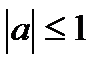 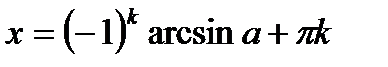 , , 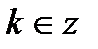 при
при 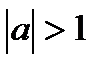 - решений нет - решений нет
| 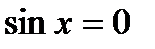 ; ; 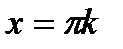 , , 
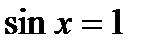 ; ; 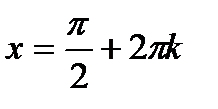 , , 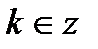
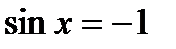 , , 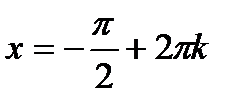 , , 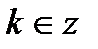
|
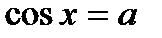
| при  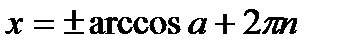 , , 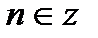 при
при 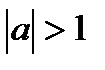 - решений нет - решений нет
| 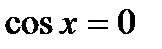 ; ; 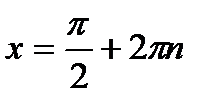 , , 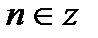
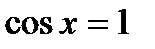 ; ; 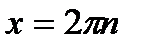 , , 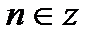
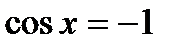 ; ; 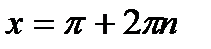 , , 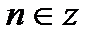
|
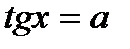
|  - любое число - любое число 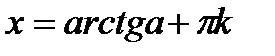 , , 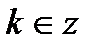
| - |
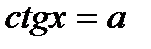
| 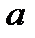 - любое число - любое число 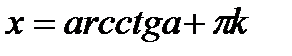 , , 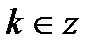
| - |
II. Тригонометрические уравнения.
| Уравнение | Способ решения | Формулы |
1. Уравнение содержит только синусы или косинусы (синусы и косинусы) вида
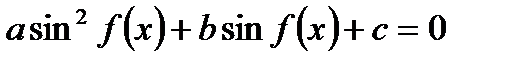
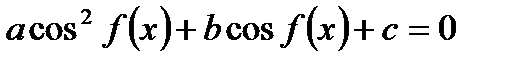 и т.д.
и т.д.
| Уравнение сводится к квадратному (биквадратному) относительно синуса (косинуса) | 
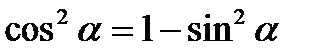
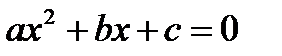
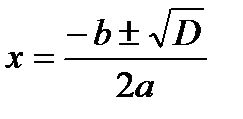
|
2. Однородное уравнение I степени вида
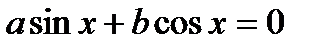
| Деление обеих частей на 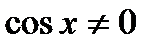 . Получаем: . Получаем: 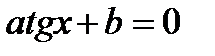
| 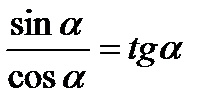
|
3. Однородное уравнение II степени вида
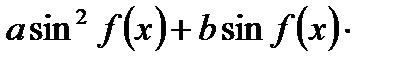
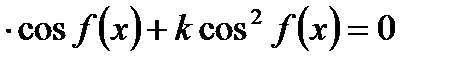
| Деление обеих частей на 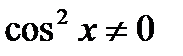 . Получаем: . Получаем: 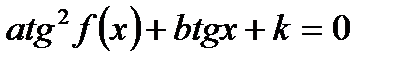
| 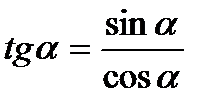
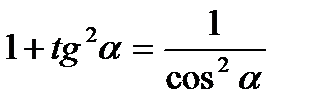
|
4. Уравнение вида
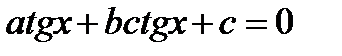
| Уравнение сводится к квадратному относительно тангенса заменой
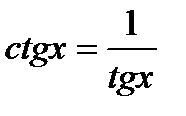
| 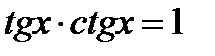
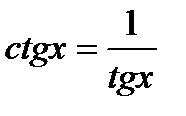
|
III. Основные тригонометрические тождества.
1. 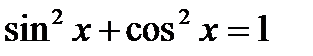 ;
; 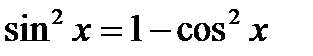 ;
; 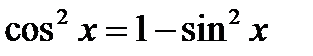
2. 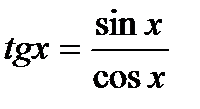
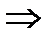
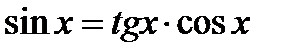
3. 
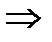
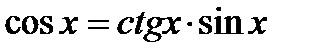
4. 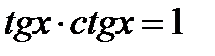
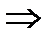
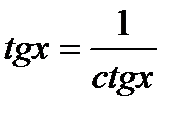 и
и 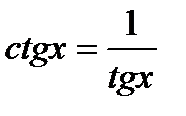
5. 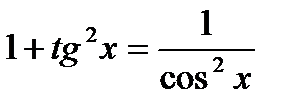
6. 
IV. Формулы сложения.
1. 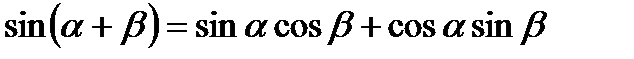
2. 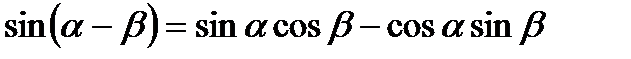
3. 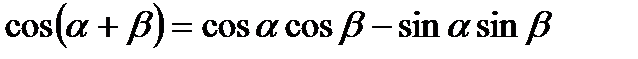
4. 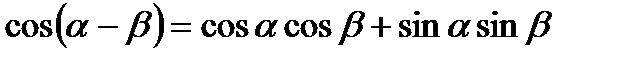
5. 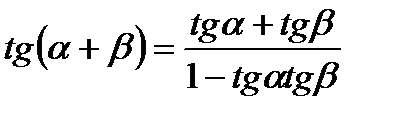
6. 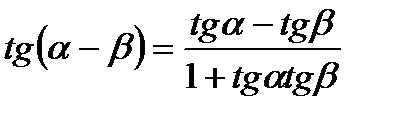
V. Формулы двойного и половинного аргументов.
1. 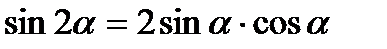
2. 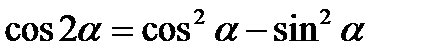 ;
; 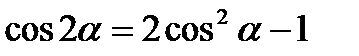 ;
; 
3. 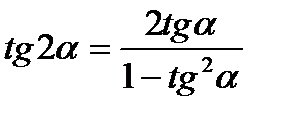
4. 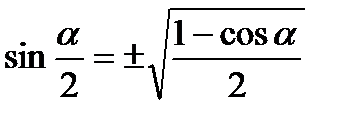
5. 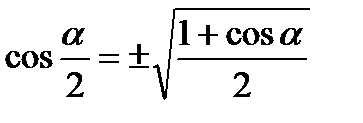
6. 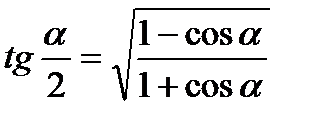
VI. Формулы суммы и разности одноименных тригонометрических функций.
1. 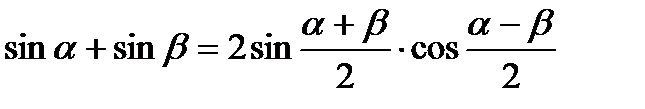
2. 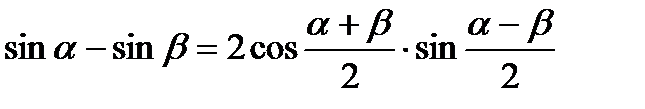
3. 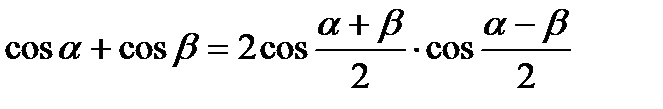
4. 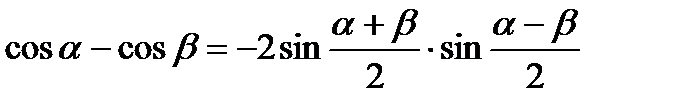
5. 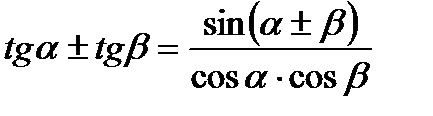
Значения тригонометрических функций
| град | 00 | 300 | 450 | 600 | 900 |
| радиан | 0 | 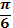
| 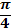
| 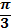
| 
|
sin 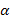
| 0 | 
| 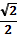
| 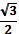
| 1 |
cos 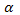
| 1 | 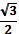
| 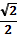
| 
| 0 |
tg 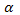
| 0 | 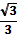
| 1 | 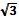
| не существ |
ctg 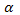
| Не существ | 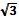
| 1 | 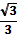
| 0 |
Используя методические рекомендации, решите уравнения:
1. 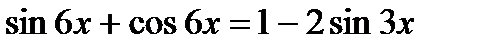 ;
;
2. 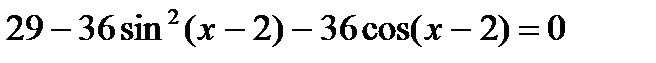 ;
;
3. 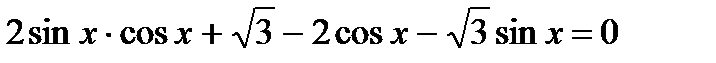 ;
;
4. 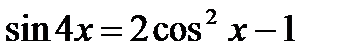 ;
;
5. 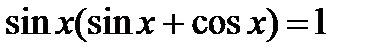 ;
;
6. 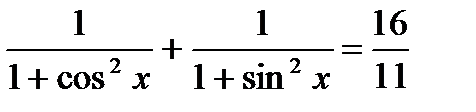 .
.
Подсказки.
1. Воспользуйтесь формулой двойного угла для 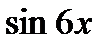 и
и 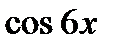 .
.
2. Обозначьте  , решите уравнение, сведя его к квадратному с помощью формулы
, решите уравнение, сведя его к квадратному с помощью формулы 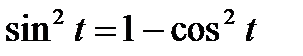 .
.
3. Сгруппируйте 1-ое и 3-е слагаемые, примените разложение на множители.
4. Воспользуйтесь формулой двойного угла для 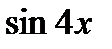 и
и 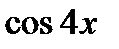 , формулой понижения степени
, формулой понижения степени 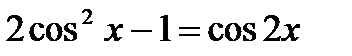 .
.
5. Раскройте скобки, примените основное тригонометрическое тождество.
6. Приведите дроби к общему знаменателю, а затем используйте основное тригонометрическое тождество 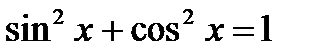 , сведите уравнение к квадратному.
, сведите уравнение к квадратному.
Тема 2. Прямые и плоскости в пространстве
Самостоятельная работа № 2.
Прямые и плоскости в пространстве
Цель: Развитие интереса к предмету.
Форма самостоятельной деятельности: создание презентации по заявленной теме.
Работа должна соответствовать методическим рекомендациям по созданию презентации.
Составление кроссворда на тему: «Взаимное расположение
 2020-04-12
2020-04-12 205
205








