Некоторые прямые задачи, в частности задачи второго типа, удобно решать в перемещениях. При этом основные уравнения следует выразить через перемещения.
Уравнения упругого равновесия в перемещениях получим путем исключения компонент тензора напряжений  (xk) из уравнений равновесия (6.3), используя формулу закона Гука (6.4).
(xk) из уравнений равновесия (6.3), используя формулу закона Гука (6.4).
Продифференцируем равенство (6.4) по координате хj:
 (6.9)
(6.9)
Учитывая, что  и
и
 (6.10)
(6.10)
а также используя дифференциальный оператор Лапласа

равенство (6.9) приводится к виду

На основании соотношения  и тогда
и тогда
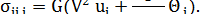 (6.11)
(6.11)
Используя равенство (6.11), дифференциальные уравнения равновесия (6.3) приводятся к виду
 (6.12)
(6.12)
Равенство (6.12) определяет три дифференциальных уравнения:
 (6.13)
(6.13)
которые представляют собой уравнения упругого равновесия в перемещениях, т. е. они выражают условия равновесия каждого элемента тела в зависимости от функций ui (xk)и  (хк), характеризующих деформированное состояние тела, и при этом учитывают соотношения между
(хк), характеризующих деформированное состояние тела, и при этом учитывают соотношения между  и
и  для однородного изотропного тела. Можно сказать, что эти уравнения отражают геометрическую, статическую и физическую стороны задачи теории упругости.
для однородного изотропного тела. Можно сказать, что эти уравнения отражают геометрическую, статическую и физическую стороны задачи теории упругости.
Уравнения (6.13), или равенство (6.12), определяющее их, называются уравнениями Ламе. Они могут быть записаны в виде одного векторного уравнения.
Умножая равенство (6.12) на орт э i и учитывая, что
 , (6.14)
, (6.14)
а также используя равенство (6.10), получим
 (6.15)
(6.15)
Уравнение (6.15) можно записать в другой, иногда более удобной, форме:
 (6.16)
(6.16)
Во многих задачах массовые силы можно считать равными нулю и тогда уравнения Ламе (6.12) принимают вид
 (6.17)
(6.17)
Продифференцировав равенство (6.17) по координате xi, получим

Отсюда, поскольку  =
=  и
и  =
=  , вытекает, что
, вытекает, что
 (6.18)
(6.18)
т. е. объемная деформация Θ (при отсутствии массовых сил или когда они постоянны) удовлетворяет уравнению Лапласа и, следовательно, Θ является гармонической функцией.
Применяя к равенству (6.17) дифференциальный оператор Лапласа и учитывая свойство (6.18), получим
 (6.19)
(6.19)
т. е. компоненты 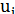 вектора перемещения являются бигармоническими функциями. Это заключение справедливо и при постоянных массовых силах, так как в этом случае при выполнении операций дифференцирования правая часть равенства (6.12) исчезает.
вектора перемещения являются бигармоническими функциями. Это заключение справедливо и при постоянных массовых силах, так как в этом случае при выполнении операций дифференцирования правая часть равенства (6.12) исчезает.
Заметим, что уравнения (6.19) не означают, конечно, что перемещения 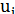 (при отсутствии массовых сил) являются произвольными бигармоническими функциями; эти функции должны удовлетворять также и дифференциальным уравнениям более низкого порядка — уравнениям Ламе (6.12).
(при отсутствии массовых сил) являются произвольными бигармоническими функциями; эти функции должны удовлетворять также и дифференциальным уравнениям более низкого порядка — уравнениям Ламе (6.12).
При решении в перемещениях основной задачи первого типа для искомых функций 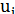 (xk) необходимо иметь условия на границе тела в зависимости от приложенных поверхностных сил.
(xk) необходимо иметь условия на границе тела в зависимости от приложенных поверхностных сил.
На основании формулы (6.4) закона Гука имеем

или, если учесть, что  =
= 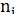 , а
, а

представляет собой производную функции 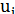 (xk) по нормали к поверхности тела, то
(xk) по нормали к поверхности тела, то
 (6.20)
(6.20)
Тогда граничные условия (6.6) принимают вид
 (6.21)
(6.21)
Уравнения Ламе (6.12) вместе с граничными условиями (6.21), т. е. в случае основной задачи первого типа, или вместе с граничными условиями (6.7) основной задачи второго типа вполне определяют все три компоненты 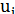 вектора перемещения. Далее, по формуле (6.1) вычисляются компоненты
вектора перемещения. Далее, по формуле (6.1) вычисляются компоненты  тензора деформации, а по формуле (6.4) находятся компоненты
тензора деформации, а по формуле (6.4) находятся компоненты  тензора напряжений.
тензора напряжений.
Совершенно ясно, что решение в перемещениях основной задачи первого типа, т. е. при граничных условиях (6.21), более затруднительно, чем решение основной задачи второго типа при значительно более простых граничных условиях (6.7). Поэтому для задач первого типа обычно предпочтительнее решение в напряжениях.
Очевидно, что уравнения движения при малых перемещениях могут быть записаны в перемещениях в любом из трех видов:
 (6.22)
(6.22)
 (6.23)
(6.23)
 (6.24)
(6.24)
В приведенных уравнениях движения перемещения 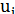 являются, естественно, функциями координат xk точек тела и времени t:
являются, естественно, функциями координат xk точек тела и времени t:  .
.
Решение уравнений движения (6.22) должно удовлетворять начальным условиям — условиям в начале движения, т. е. при t = 0 перемещения 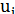 и их производные по времени t (скорости
и их производные по времени t (скорости 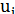 ) должны иметь заданные значения
) должны иметь заданные значения  и
и  :
:
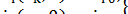 (6.25)
(6.25)
 2020-04-20
2020-04-20 403
403








