Общее решение уравнений в перемещениях

Общее решение уравнений Ламе было получено П. Ф. Папковичем (1887—1946) в 1932 г., а позднее (1934) другим путем получил Нейбер.

При равновесии однородного изотропного тела в случае отсутст­вия массовых сил уравнения Ламе определяются равенством (6.17). Решение этих уравнений будем искать в следующем виде:

                                                                                                (6.26)

где φ_i (i = 1, 2, 3) — гармонические функции, т. е.  = 0; ψ — некоторая скалярная функция, подлежащая определению. В соответствии с (6.26) объемная деформация

                                         (6.27)

Подставляя в уравнения Ламе (6.17) выражения для  и в по фор­мулам (6.26) и (6.27) и учитывая, что  = 0, найдем

или

                                                     (6.28)

Легко видеть, что последнее равенство будет удовлетворяться, ес­ли функцию ψ подчинить уравнению

                                                                          (6.29)

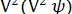Так как = 0 и  = = 0, то из уравнения (6.29) следует, что функция ψ должна быть бигармонической, т. е. должна удовлетворять уравнению =  = 0.

Любая гармоническая функция  является также и бигармони­ческой функцией:

                                                             (6.30)

Можно показать, что если — гармонические функции, то функ­ции

                           (6.31)

будут бигармоническими.

Действительно, рассмотрим, например, первую функцию (6.31). Поскольку

то, учитывая, что , получим

 (6.32)

и, следовательно,

                      (6.33)

Из равенства (6.33) следует, в частности, что производная гармо­нической функции есть также гармоническая функция.

На основании (6.31) частное решение уравнения (6.29) примем в следующем виде:

                                                            (6.34)

где С — постоянная.

Последовательно дифференцируя равенство (6.34), найдем

                        (6.35)

Свертывая последнее равенство по индексам i и j и учитывая, что 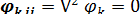, получим

                                                              (6.36)

Из сопоставления равенств (6.29) и (6.36) находим

                                                                               (6.37)

Общее решение уравнения (6.29) должно представляться суммой его частного решения (6.34) и произвольной гармонической функции , т. е.

                                               (6.38)

Тогда общее решение уравнений Ламе (6.17) на основании (6.26) и (6.36) будет выражено через четыре произвольные, независимые друг от друга гармонические функции ,  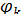(k = 1, 2, 3):

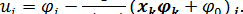                                         (6.39)

 

Однако это равенство правильнее называть не общим решением уравнений Ламе, а функциональным представлением в форме Папко-вича—Нейбера вектора перемещения и в упругом изотропном одно­родном теле.

В представлении Папковича — Нейбера (6.39), не нарушая его общ­ности, как было показано в работах М. Г. Слободянского (1954), Р. Юбенкса и Е. Стернберга (1956), можно сохранить только три гар­монические функции, т. е. принять его в таком виде:

                                                 (6.40)

Но в случае конечной односвязной области последнее представление допустимо при условии, что υ  0,25.

В некоторых случаях сохранение функции  в (6.39) оказывается полезным, поскольку за счет произвольного ее выбора можно до­стигнуть упрощения выкладок при решении конкретной задачи.

Исходя из (6.26) и учитывая (6.35), (6.37), получим формулу для компонент тензора относительного перемещения:

                               (6.41)

Свертывая последнее равенство по индексам i и j и вспоминая, что 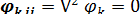, найдем

                                                                        (6.42)

 

Подставив теперь равенства (6.41) и (6.42) в формулу закона Гука (6.4), получим представление компонент тензора напряжений через гармонические функции :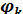

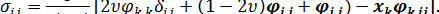            (6.43)