Основные задачи статики упругого тела

Основные уравнения и задачи теории упругости

 

Основные уравнения

Вначале дадим общую сводку основных уравнений для задач рав­новесия упругого тела, которые составляют содержание раздела тео­рии упругости, называемого обычно статикой упругого тела.

Деформированное состояние тела вполне определяется тензором поля деформации  или полем перемещений . Компоненты тензора деформации  связаны с перемещениями  дифференциальными зависимостями Коши:

                                                                            (6.1)

Компоненты тензора деформации должны удовлетворять дифферен­циальным зависимостям Сен-Венана:

                                                       (6.2)

которые являются необходимыми и достаточными условиями интег­рируемости уравнений (6.1).

Напряженное состояние тела определяется тензором поля напря­жений  Шесть независимых компонент симметричного тензора (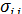) должны удовлетворять трем дифференциальным уравне­ниям равновесия:

                                                                             (6.3)

Компоненты тензора напряжений 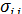 и перемещения  связаны шестью уравнениями закона Гука:

                                            (6.4)

где

.

В некоторых случаях уравнения закона Гука приходится исполь­зовать в виде формулы

                                                          (6.5)

где

Уравнения (6.1)—(6.5) являются основными уравнениями стати­ческих задач теории упругости. Иногда уравнения (6.1) и (6.2) на­зывают геометрическими уравнениями, уравнения (6.3) — статиче­скими уравнениями, а уравнения (6.4) или (6.5) — физическими урав­нениями.

К основным уравнениям, определяющим состояние линейно-упруго­го тела в его внутренних точках объема V, необходимо присоединить условия на его поверхности S. Эти условия называются граничными условиями. Они определяются либо заданными внешними поверхност­ными силами ti, либо заданными перемещениями ^(s) точек поверх­ности тела. В первом случае граничные условия выражаются равен­ством:

                                                                (6.6)

где 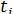 (x_s) — компоненты вектора t поверхностной силы,  — компо­ненты единичного вектора п, направленного по внешней нормали к поверхности S в рассматриваемой ее точке.

Во втором случае граничные условия выражаются равенством

= ^(s),                                                                   (6.7)

где ^(s) = ^(s)(х_s) — заданные на поверхности функции.

Граничные условия могут также иметь смешанный характер, когда на одной части S_t поверхности тела заданы внешние поверхностные си­лы t_i (x_s), а на другой части S_u поверхности тела заданы перемещения

^(s)(x_s):

                                                                                (6.8)

 

Возможны и иного рода граничные условия. Например, на некото­ром участке поверхности тела заданы только некоторые компоненты  вектора перемещения и, кроме того, также не все компоненты 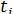 вектора поверхностной силы.

 

Основные задачи статики упругого тела

В зависимости от вида граничных условий различают три типа ос­новных статических задач теории упругости.

Основная задача первого типа состоит в опре­делении компонент тензора поля напряжений 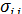 (x_k) внутри области V, занятой, телом, и компонент  (x_k) вектора перемещения точек внутри области V и точек поверхности S тела по заданным массовым силам f_i и поверхностным силам t_i.

Искомые девять функций должны удовлетворять основным уравне­ниям (6.3) и (6.4), а также граничным условиям (6.6).

Основная задача второго типа состоит в определении перемещений u_i (x_k) точек внутри области V и компонент тензора поля напряжений 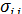 (x_k)  по заданным массовым силам f_i и по заданным перемещениям  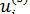(x_s) на поверхности тела.

Искомые функции u_i (x_k) и 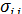 (x_k) должны удовлетворять основным уравнениям (6.3) и (6.4) и граничным условиям (6.7).

Заметим, что граничные условия (6.7) отражают требование о непре­рывности определяемых функций u_i (x_k) на границе S тела, т. е. когда внутренняя точка М (x_k) стремится к некоторой точке поверхности S, функция u_i (x_k) должна стремиться к заданному значению 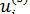 (x_s)  в данной точке поверхности.

Основная задача третьего типа или смешан­ная задача состоит в том, что по заданным поверхностным си­лам t_i (x_s) на одной части поверхности тела S_t и по заданным переме­щениям 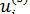 (x_s)  на другой части поверхности тела S_u, а также, вообще говоря, по заданным массовым силам f_i требуется определить компо­ненты тензора напряжений  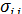(x_k)  и перемещения u_i (x_k), удовлетво­ряющие основным уравнениям (6.3) и (6.4) при выполнении смешан­ных граничных условий (6.8).

Получив решение данной задачи, можно определить, в частности, усилия связей на S_u, которые должны быть приложены в точках по­верхности S_u, чтобы реализовать заданные перемещения 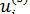 (x_s)  на этой поверхности, а также можно вычислить перемещения u_i то­чек поверхности S_t.