Типи трендових моделей

При моделюванні динамічних процесів причинний механізм формування властивих їм особливостей у явному вигляді не враховується. Будь-який процес розглядається як функція часу. Певна річ, час не є фактором конкретного соціально-економічного процесу, змінна часу t просто акумулює комплекс постійно діючих умов і причин, які визначають цей процес.

У моделях динаміки процес умовно поділяється на чотири складові:

- довгострокову, детерміновану часом еволюцію — тренд f(t));

- періодичні коливання різних частот C_t;

- сезонні коливання S_t;

- випадкові коливання e_t.

Зв'язок між цими складовими представляється адитивно (сумою) або мультиплікативно (добутком):

 

 

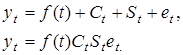
Така умовна конструкція дає змогу, залежно від мети дослідження, вивчати тренд, елімінуючи коливання, або вивчати коливання, елімінуючи тренд. При прогнозуванні здійснюється зведення прогнозів різних елементів в один кінцевий прогноз.

Характерною властивістю будь-якого динамічного ряду є залежність рівнів: значення у_t , певною мірою залежить від попередніх значень: 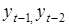 i т. д. Для оцінювання ступеня залежності рівнів ряду використовують коефіцієнти автокореляції r_р з часовим лагом p = 1, 2,..., т.

Коефіцієнт r_р характеризує щільність зв'язку між первинним рядом динаміки і цим же рядом, зсуненим на p моментів. У табл. 2.1 наведено зсунені ряди динаміки з лагами p - 1, 2, 3. Як видно, із збільшенням лага p кількість пар корельованих рівнів зменшується. Так, при p = 1 довжина корельованих рядів менша за первинний ряд на один рівень, при p = 2 — на два рівні і т. д. Через це на практиці при визначенні автокореляційної функції дотримуються правила, за яким кількість лапв .

Таблиця 2.1

Змінна часу t	Рівень ряду у	р=1	р = 2	р = 3
1		—	—	—
2			—	—
З				—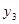
…	…	…	…	…
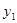
n-2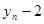
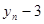
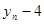
n-1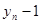
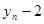
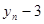
n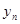

 

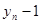
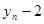
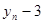
Значення коефіцієнта автокореляції r_р визначається величиною лага p і не виходить за межі ±1:

 

де

 

Послідовність коефіцієнтів r_р називають автокореляційною функцією і зображують графічно у вигляді автокорелограми з абсцисою p та ординатою r_p.

За швидкістю згасання автокореляційної функції можна зробити висновок про характер динаміки. Найчастіше використовується значення r₁. Характеризуючи ступінь залежності двох послідовних членів ряду, коефіцієнт автокореляції є мірою неперервності цього ряду. Якщо , то ряду динаміки властива тенденція розвитку, якщо 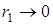 — рівні ряду незалежні. Відносно високі значення коефіцієнта автокореляції при p = k, 2k, 3k, … свідчать про регулярні коливання.

На відміну від детермінованої складової випадкова складова не зв'язана із зміною часу. Аналіз цієї складової є основою перевірки гіпотези про адекватність моделі реальному процесу. За умови, що модель вибрано правильно, випадкова складова являє собою стаціонарний процес з математичним сподіванням M(e) = 0 і дисперсією

 

 

де m — число параметрів функції.

Для оцінювання стаціонарності випадкової складової використовують циклічний коефіцієнт автокореляції першого порядку r₁. Корелюються ряди залишкових величин:  та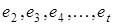

Припускаючи, що , формула розрахунку спрощується:

 

.

 

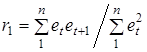Існують таблиці критичних значень циклічного коефіцієнта автокореляції для додатних і від'ємних значень (додаток 5). Якщо фактичне значення r₁ менше за критичне, автокореляція вважається неістотною, а випадкова складова — стаціонарним процесом. У разі, коли фактичне значення r₁ перевищує критичне, можна зробити висновок про неадекватність детермінованої складової реальному процесу.

Важливою складовою динамічних процесів є тенденція середньої, тобто основний напрям розвитку. B аналізі динамічних рядів тенденцію представляють у вигляді плавної траєкторії та описують певною функцією, яку називають трендом Y_t = f(t), де t= 1, 2, …, n — змінна часу. Ha основі такої функції здійснюється вирівнювання динамічного ряду і прогнозування подальшого розвитку процесу.

Процедура вирівнювання динамічних рядів включає два етапи: обґрунтування (вибір) типу функції, яка б адекватно описувала характер динаміки, та оцінювання параметрів функції. Ha практиці переважно використовують функції, параметри яких мають конкретну інтерпретацію залежно від характеру динаміки. Найбільш поширені поліноми (многочлени), різного роду експоненти та логістичні криві. Так, параметри полінома p -ro ступеня Y_t = a + bt + ct² + dt³… характеризують:

а — рівень динамічного ряду при t = 0;

b — абсолютну швидкість зміни рівнів ряду (ординат);

2c — прискорення (прирощення абсолютної швидкості);

d — зміну прирощення тощо.

Поліном 1-го ступеня, тобто лінійний тренд Y_t = a + bt, описує процеси, які рівномірно змінюються в часі і мають стабільні прирости ординат. Поліном 2-го ступеня (парабола) Y_t = a + bt + ct² здатний описати процес, характерною особливістю якого є рівноприскорене зростання або зменшення ординат. Форма параболи визначається параметром c: при c > 0 гілки параболи спрямовані вгору — парабола має мінімум, при c < 0 гілки параболи спрямовані вниз — парабола має максимум. При визначенні екстремуму (max, min) похідну параболи прирівнюють до нуля і розв'язують систему рівнянь відносно t. Наприклад, динаміка захворювань при епідемії грипу (чол.) описується параболою Y_t = 264 + 45t - 1,5t². Похідна параболи 45-2,25t = 0, a t = 20. Максимум захворювань буде зафіксовано через 20 днів від початку відліку часу (t = 0) і становитиме Y_mах = 264 + 45 – 20 - 1,5 × 20²  = 564 чол. У полінома 3-го ступеня Y_t = a + bt + ct² + dt³ знак прирощення ординати може змінюватися один чи два рази.

Якщо характерною властивістю процесу є стабільна відносна швидкість (темпи приросту), такий процес описується експонентою яка може набувати різних еквівалентних форм. Основна (показникова) форма експоненти

Y_t = ab^t

 

де b — середня відносна швидкість зміни ординати: при b > 1 ордината зростає з постійним темпом, при b < 1, навпаки, зменшується. Абсолютний приріст пропорційний досягнутому рівню. Експоненту можна представити у формі:

 

 або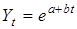

 

де l = ln b, е = 2,718 — основа натурального логарифма, ln e = 1.

Експоненти приводяться до лінійного виду заміною y_t десятковими або натуральними логарифмами:

 

lg Y =lg a + t lg b, |

ln Y = ln a + lt ln e = ln a + lt,

ln Y = ln e^a + ln e^bt = ln a + ln bt = ln a + lt.

 

Оцінювання параметрів трендових рівнянь найчастіше здійснюється методом найменших квадратів (MHK), основною умовою якого є мінімізація суми квадратів відхилень фактичних значень y_t від теоретичних Y_t, визначених за трендовим рівнянням:

 

.

 

Параметри поліноміального тренда визначаються безпосередньо розв'язуванням систем p + 1 нормальних рівнянь. Експонента, як показано вище, приводиться до лінійного виду логарифмуванням; розраховані параметри підлягають потенціюванню.

Виявлену тенденцію можна продовжити за межі динамічного ряду Така процедура називається екстраполяцією тренда. Принципова можливість екстраполяції ґрунтується на припущенні, що умови, які визначали тенденцію у минулому, не зазнають істотних змін у майбутньому. Формально операцію екстраполяції можна представити як визначення функції:

 

,

 

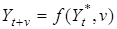де Y_t+v — прогнозне значення на період упередження v;  — база екстраполяції, найчастіше це останній, визначений за трендом рівень ряду.

Екстраполяція тренда дає точковий прогноз. Очевидно, що «влучення в точку» малоймовірне. Адже тренду властива невизначеність, передусім через похибки параметрів. Джерелом цих похибок є обмежена сукупність спостережень y_t, кожне з яких містить випадкову компоненту e_t,. Зсунення періоду спостереження лише на один крок веде до зсунення оцінок параметрів. Випадкова компонента буде присутня і за межами динамічного ряду, а отже, її необхідно врахувати. Для цього визначають довірчий інтервал, який би з певною ймовірністю окреслив межі можливих значень Y_{t + v} Точковий інтервал перетворюється в інтервальний. Ширина інтервалу залежить від варіації рівнів динамічного ряду навколо тренда та ймовірності висновку (1 - а):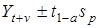

Де S_p — середня квадратична похибка прогнозу, значення якої залежить від дисперсії тренда   та дисперсії відхилень від тренда . Зокрема, для лінійного тренда

.

 

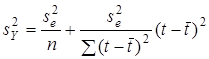Якщо база прогнозування — останній рівень ряду, то 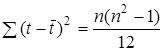, a 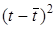 замінюється на 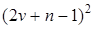. Після нескладних алгебраїчних перетворень похибку прогнозу за лінійним трендом можна представити так:

 

 

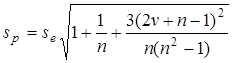
або, позначивши підкореневий вираз символом z, s_p = s_ez.

Тобто похибка прогнозу залежить від залишкової дисперсії , довжини динамічного ряду (передісторії) n та періоду упередження v. Чим довший період передісторії, тим похибка менша, а збільшення періоду упередження, навпаки, веде до зростання похибки прогнозу.