Определение и классификация точек разрыва функции

         Точка 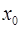 называется точкой разрыва функции , если  в точке 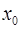 не является непрерывной.

    Точка 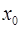 называется точкой разрыва го рода, если в этой точке функция  имеет конечные, но не равные друг другу правый и левый пределы.

    Точка 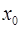 называется точкой разрыва го рода, если в этой точке функция не имеет по крайней мере одного из односторонних пределов или если хотя бы один из односторонних пределов бесконечен.

Кусочно-непрерывные функции.

         Функция  называется кусочно-непрерывной на отрезке если она непре­рыв­на во всех внутренних точках за исключением, быть может, конечного числа то­чек, в которых имеет разрыв го рода и, кроме того, имеет односторонние пределы в точках и .

    Функция называется кусочно-непрерывной на интервале или бесконечной прямой, если она кусочно-непрерывна на любом принадлежащем им отрезке.

Свойства непрерывных функций.

1. Теорема об устойчивости знака непрерывной функции.

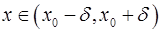· Пусть функция определена в некоторой точке  и . Тогда существует такое, что для всех  функция имеет тот же знак, что .

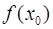2. Теорема о прохождении непрерывной функции через нулевое значение при смене знаков.

· Пусть функция непрерывна на отрезке 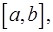 и на концах имеет значения разных знаков. Тогда существует точка , в которой .

3. Теорема о прохождении непрерывной функции через любое проме­жуточ­ное значение.

· Пусть функция непрерывна на отрезке и число  лежит между  и . Тогда существует точка  такая, что .

· Если функция  определена и непрерывна на некотором промежутке , то множество ее значений  тоже представляет некоторый промежуток.

4. Теорема об ограниченности непрерывной функции на отрезке.

· Если функция  определена и непрерывна на отрезке  то она ограничена на этом отрезке.