1). Свойство вписанного четырехугольника: сумма противоположенных углов равна 180°. В окружность можно вписать: квадрат (R равен половине диагонали), прямоугольник (R равен половине диагонали), равнобедренную трапецию и правильный шестиугольник (R равен стороне)
2). Свойство описанного четырехугольника: суммы противоположенных сторон равны.
Около окружности можно описать квадрат (r равен половине стороны), ромб
(r равен половине высоты) и правильный шестиугольник.

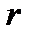
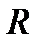

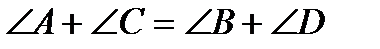 =180º
=180º 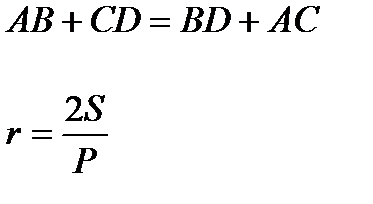
3). Квадрат Правильный шестиугольник

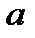
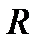
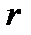
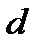
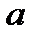

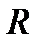
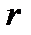
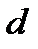
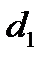
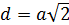
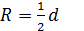
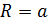
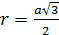
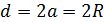
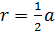
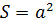
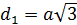
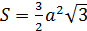
Правильные многоугольники
Сумма углов выпуклого n- угольника равна 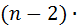 180
180 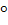 ,
,
где 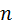 – количество сторон многоугольника.
– количество сторон многоугольника.
Правильный многоугольник – многоугольник, у которого равны все стороны и углы.
Угол правильного n- угольника равен 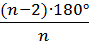 ,
,
где 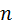 – количество сторон многоугольника.
– количество сторон многоугольника.
5. Опорные задачи.
1). Свойство ромба с углом 60°:
если в ромбе один из углов равен 60°, то у него меньшая диагональ равна стороне.
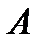
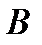
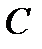
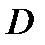
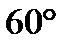
Если 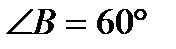 , то АC = AB.
, то АC = AB.
2). Дополнительные свойства диагоналей параллелограмма:
а) сумма квадратов диагоналей в параллелограмме равна сумме квадратов всех его сторон
б) при проведении диагоналей в параллелограмме площади полученных треугольников равны
B C
 C
C 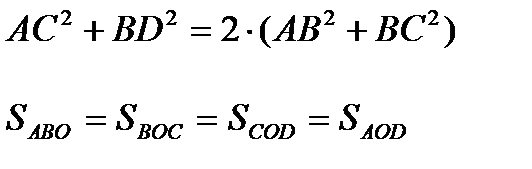
O
A D
3). Свойство углов в четырехугольнике: сумма углов в четырехугольнике равна 360°.
4). Свойства биссектрис в параллелограмме:
а) биссектриса угла в параллелограмме (в прямоугольнике или трапеции) отсекает равнобедренный треугольник.
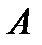
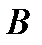
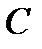
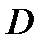
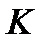

если АК – биссектриса угла А (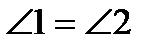 ),
),
то AB = BK
б). в параллелограмме биссектрисы смежных углов перпендикулярны,в трапеции биссектрисы углов, прилежащих к боковым сторонам перпендикулярны
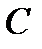
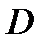
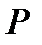
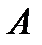
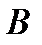
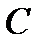
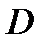
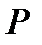


Если AP и DP –биссектрисы углов, то 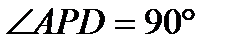
5). Свойства треугольников, образованных при пересечении диагоналей в трапеции:
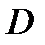
 a) Δ AOD
a) Δ AOD 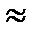 Δ BOC
Δ BOC
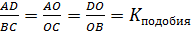
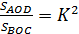
б) 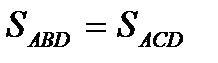 и
и 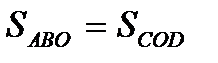
6). Свойство отрезка, соединяющего середины диагоналей трапеции:
середины диагоналей трапеции лежат на средней линии, а отрезок, соединяющий эти точки равен полу разности основании.
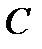
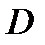
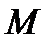

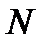
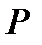
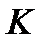

если P и K – середины диагоналей, то 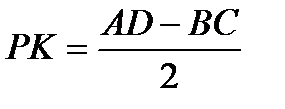
7). Свойство равнобедренной трапеции: 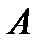
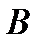
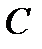
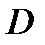
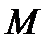



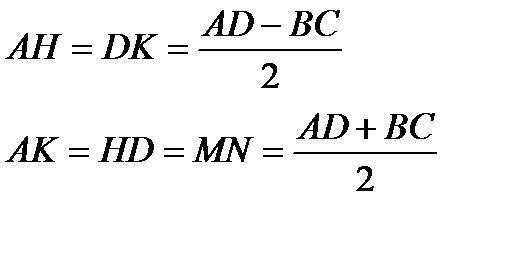
8). Свойство равнобедренной трапеции со взаимно перпендикулярными диагоналями: в равнобедренной трапеции с перпендикулярными диагоналями высота равна средней линии.
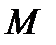
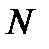

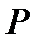
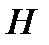


 если AB = CD и BD
если AB = CD и BD 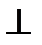 AC,
AC,
то MN = PH
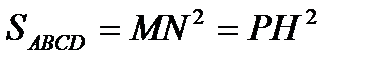
5. Площадь любого многоугольника
Площадь любого многоугольника можно найти без применения формул
Надо вписать фигуру в прямоугольник, посчитать общую площадь прямоугольника по клеточкам, посчитать площадь прямоугольных треугольников, которые дополняют фигуру до прямоугольника и вычесть из площади прямоугольника площади всех треугольников.
| 1 | |||||||||
| 2 | |||||||||
| 3 | |||||||||
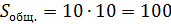
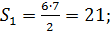
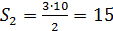
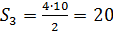
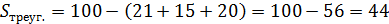
Тема 1.5. Окружность
1. Центральные и вписанные углы.
1). Свойства центральных и вписанных углов:
центральный угол равен дуге, на которую он опирается вписанный угол равен половине дуги, на которую он опирается


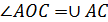
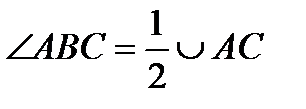
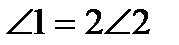
2). Свойство углов, опирающихся на одну дугу: углы, опирающиеся на одну дугу равны.
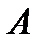
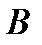
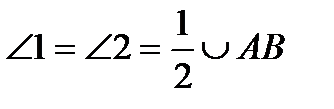
3). свойство вписанного угла, опирающегося на диаметр:
угол, опирающийся на диаметр – прямой.
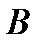
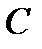

 если АВ – диаметр, то
если АВ – диаметр, то 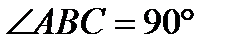
если 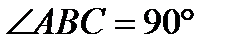 , то АВ – диаметр.
, то АВ – диаметр.
2. Длина окружности и площадь круга и его частей
круг сектор кольцо
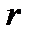
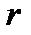
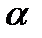
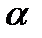
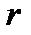
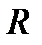
c =2 π r (длина окружности) l = 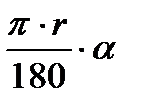 (длина дуги)
(длина дуги) 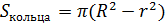
S =π 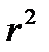 (площадь круга) S =
(площадь круга) S = 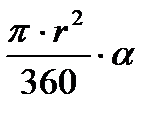 (площадь сектора)
(площадь сектора)
3. Касательная к окружности.
1). Свойство касательной к окружности: касательная к окружности перпендикулярна к радиусу, проведенному в точку касания
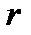
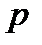
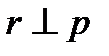

2). Свойство касательных, проведенных к окружности из одной точки:
отрезки касательных, проведенные из одной точки, равны и
составляют равные углы с отрезком, соединяющим эту точку с
центром окружности
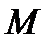
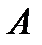
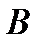

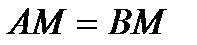
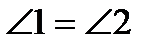

3). Свойство касательной и хорды, проведенных из одной точки:
угол между касательной и хордой равен половине дуги,
заключенной между ними. 
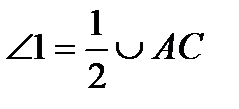
5. Опорные задачи.
1 ). Свойства пересекающихся хорд: произведение отрезков хорд равны.

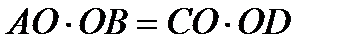
2 ). Свойство диаметра и хорды: диаметр окружности,
перпендикулярный к хорде, делит эту хорду пополам,

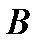
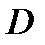
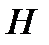

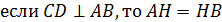
3). Свойство перпендикуляра, проведенного к диаметру:
перпендикуляр, проведенный из любой точки окружности к
диаметру, есть среднее пропорциональное между отрезками,
на которые перпендикуляр делит диаметр.
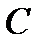


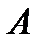
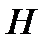
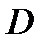
 если
если 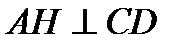 , то
, то 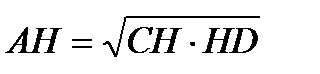
6). Свойство секущих, проведенных из одной точки к окружности
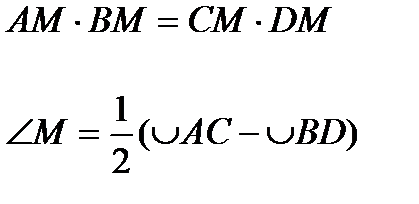
7). Свойство секущей и касательной, проведенных из одной точки
к окружности
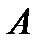
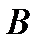
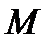
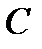
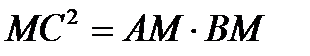
8). Длина хорды и площадь сегмента и сектора:
Сегмент – часть круга, ограниченная хордой и дугой окружности
Сектор – часть круга, ограниченная двумя радиусами и дугой окружности
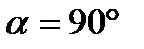
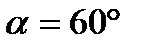
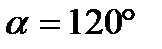



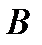
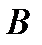
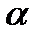
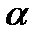
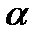
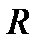
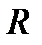
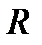
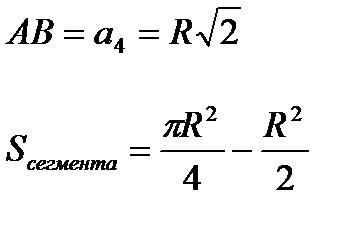
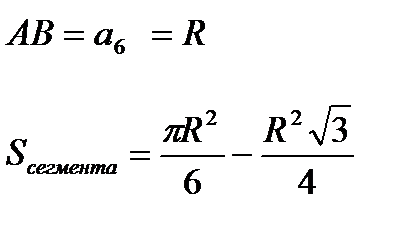
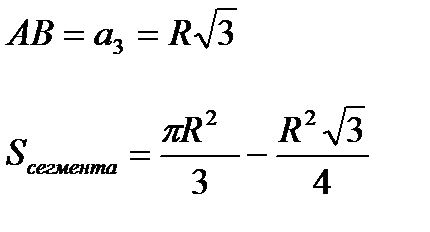
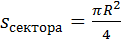
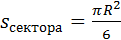
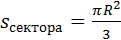
9). Связь длины хорды и расстояния ее от центра окружности:
хорда большей длины расположена ближе к центру.
 2020-04-20
2020-04-20 493
493








