2020-04-20
118
2.4. Численные характеристики законов распределения. Моменты
Полная информация, которую дают о случайной погрешности её законы распределения, в большинстве случаев бывает излишней. Кроме того, многие законы распределения имеют громоздкие математические выражения и неудобны для практических расчётов. Поэтому на практике чаще используют отдельные численные характеристики законов распределения. Наибольшее распространение получили численные характеристики, называемые моментами.
Начальным моментом k-го порядка называют величину
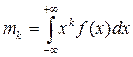, (2.11)
где f (x) – плотность распределения случайной величины x.
Начальный момент первого порядка называют математическим ожиданием M (x):
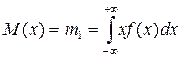. (2.12)
Математическое ожидание является характеристикой центра распределения случайной погрешности.
Центральным моментом k-го порядка называется величина
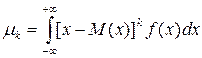, (2.13)
где M (x) – математическое ожидание случайной величины x.
|
|
|
Центральный момент первого порядка для любого закона распределения равен нулю, поэтому не используется на практике.
Центральный момент второго порядка называется дисперсией D (x):
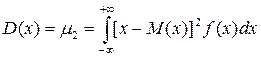. (2.14)
Дисперсия является характеристикой рассеяния случайной погрешности относительно центра распределения – математического ожидания. Дисперсия имеет размерность квадрата случайной погрешности, поэтому её использование не всегда бывает удобно. Чаще для характеристики рассеяния случайной погрешности используют величину, равную квадратному корню из дисперсии, которая называется среднеквадратическое отклонение (СКО) s (x):
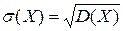. (2.15)
Иногда применяют числовые характеристики законов распределения, которые не являются моментами. Подобными характеристиками являются мода и медиана.
Модой Mo (x) называют значение случайной величины, которому соответствует максимум плотности распределения.
Медианой Me (x) случайной величины называют такое её значение, для которого функция распределения равна 0,5. Геометрически медиана представляет собой абсциссу точки, которая делит площадь, ограниченную кривой плотности распределения, пополам.
2.5. Нормальный закон распределения случайной погрешности
Согласно центральной предельной теореме теории вероятностей, сумма бесконечно большого числа бесконечно малых случайных возмущений с произвольными законами распределения подчиняется нормальному закону распределения. Применительно к теории погрешностей это означает, что нормальное распределение случайных погрешностей возникает, когда на результат измерения действует множество случайных возмущений, ни одно из которых не является преобладающим. На практике суммирование даже небольшого числа возмущений (не менее трёх) приводит к закону распределения случайной погрешности, близкому к нормальному.
|
|
|
Плотность f (x) и функция F (x) распределения нормального закона описываются выражениями:
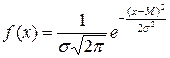; (2.16)
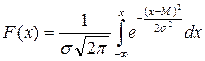, (2.17)
где: M и s – соответственно, математическое ожидание и СКО закона распределения.
Графики соответствующих зависимостей представлены на рис. 2.8.
Положение кривой плотности распределения и её форма определяются значениями математического ожидания и СКО. С изменением математического ожидания форма кривой не изменяется, но меняется её положение относительно начала координат (рис. 2.9).
С изменением СКО положение кривой не меняется, но меняется её форма (рис. 2.10).
Для удобства представления в табличном виде нормальный закон распределения обычно представляют в нормированном виде.
Нормированной называется случайная величина z
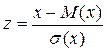. (2.18)
Для нормированной случайной величины M (z) = 0 и s (z) = 1. Подставив соответствующие значения в (2.16) и (2.17), получим выражения для нормального закона распределения в нормированной форме:
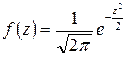; (2.19)
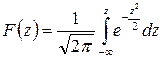. (2.20)
Иногда нормальный закон распределения задается в виде интеграла Лапласа (функции ошибок):
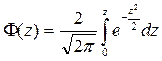, (2.21)
который связан с нормированной функцией нормального распределения соотношением
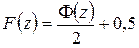. (2.22)
Рис. 2.8. Плотность f(x) и функция F(x) нормального закона распределения
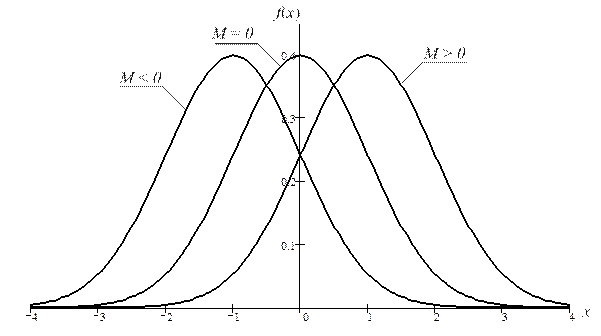
Рис. 2.9. Зависимость кривой плотности распределения от величины математического ожидания
Рис. 2.10. Зависимость кривой плотности распределения от величины среднеквадратического отклонения
2.6. Равномерный закон распределения случайной погрешности
Случайная погрешность подчиняется равномерному закону распределения, если она может принимать значения только в пределах некоторого конечного интервала, причем с одинаковой вероятностью.
Плотность распределения равномерного закона распределения имеет вид
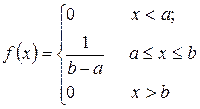. (2.23)
где a и b – границы закона распределения.
Функция распределения равномерного закона
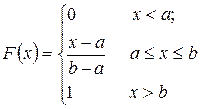. (2.24)
Графики плотности и функции распределения равномерного закона представлены на рис. 2.11.
Математическое ожидание равномерного закона распределения
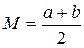. (2.24)
Дисперсия и СКО
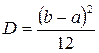; (2.25)
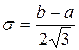. (2.26)
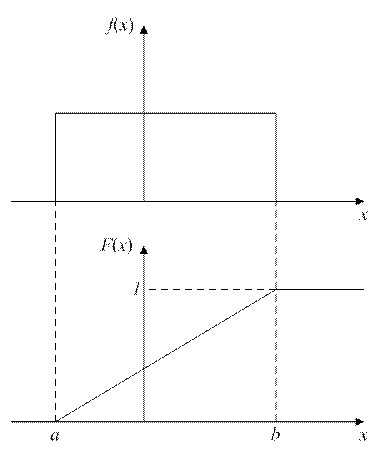
Рис. 2.11. Графики плотности f(x) и функции F(x) распределения равномерного закона
2.7. Треугольный закон распределения случайной погрешности
(закон Симпсона)
Треугольный закон распределения (закон Симпсона) возникает при суммировании двух равномерно распределённых случайных погрешностей с равными дисперсиями.
Плотность распределения треугольного закона:
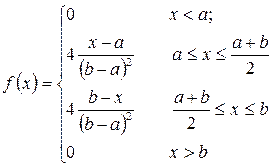(2.27)
Функция распределения треугольного закона
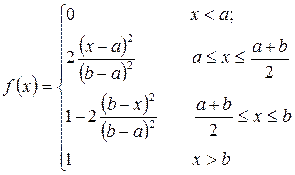. (2.28)
Графики плотности и функции распределения равномерного закона представлены на рис. 2.12.
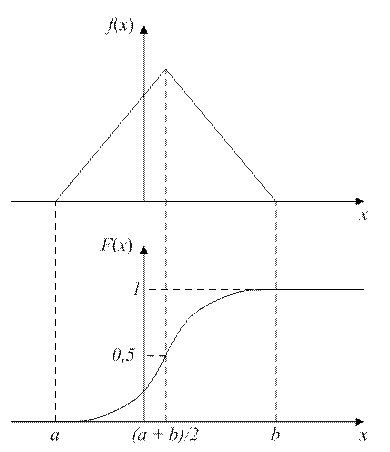
Рис. 2.12. Графики плотности f(x) и функции F(x) распределения треугольного закона распределения
Математическое ожидание треугольного закона распределения
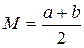. (2.29)
Дисперсия и СКО
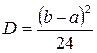; (2.30)
|
|
|
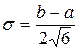. (2.31)
2.8. Оценки результатов и погрешностей измерений
При наличии в результате измерения случайной погрешности определить точное значение измеряемой величины невозможно принципиально, поэтому задача обработки результатов измерений заключается в нахождении оценок измеряемых величин и их погрешностей.
Оценкой какой-либо величины называют её значение, вычисленное на основе экспериментально полученных результатов.
Поскольку количество результатов, обрабатываемых для получения оценок, всегда ограничено, то оценка является случайной величиной. Оценки принято обозначать той же буквой, что и оцениваемые величины, но с добавлением «волны» или «крышки» над ней: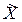 
; 
.
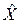К оценкам предъявляется ряд требований, таких, как состоятельность, несмещённость и эффективность.
Оценка называется состоятельной, если при увеличении числа наблюдений она стремится к оцениваемой величине: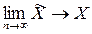 
Оценка называется несмещённой, если её математическое ожидание равно оцениваемой величине: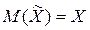 
.
Оценка называется эффективной, если она имеет наименьшую, по сравнению с другими оценками той же величины, дисперсию: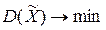 
.
Различают точечные и интервальные оценки.
Точечная оценка представляет собой отдельное число (точку на числовой оси). Примерами точечных оценок являются:
оценка математического ожидания – среднее арифметическое наблюдений:
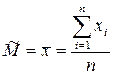. (2.32)
оценка дисперсии:
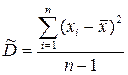. (2.33)
Вышеприведённые оценки математического ожидания и дисперсии являются состоятельными и несмещёнными. Их эффективность зависит от закона распределения результатов наблюдений. Иногда в расчётах применяют смещённую оценку дисперсии:
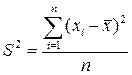. (2.34)
Недостатком точечных оценок является то, что они не дают информации, как далеко от оценки может находиться истинное значение оцениваемой величины и с какой вероятностью. Более информативными являются интервальные (квантильные) оценки. Примером интервальной оценки является доверительный интервал с указанием доверительной вероятности попадания в этот интервал.
|
|
|
Q-процентной квантилью распределения понимают абсциссу вертикальной линии, слева от которой площадь под кривой плотности распределения f (x) равна q %.
Для примера на рис. 2.13 показаны пяти- и девяноста пятипроцентные квантили распределения. Из рисунка видно, что в интервал между x0,05 и x0,95 попадают 90 % всех значений случайной величины x, следовательно, указанные квантили распределения ограничивают доверительный интервал для вероятности 90 % (P = 0,9).
В метрологии, как правило, используют симметричные законы распределения. Для них квантильная вероятность q связана с доверительной вероятностью Pд соотношением
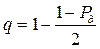. (2.36)
Поскольку от принятого значения доверительной вероятности зависит величина доверительного интервала, её указывают при записи результатов измерений.
В большинстве случаев при оценке погрешности результатов измерения нормативными документами рекомендуется принимать доверительную вероятность Pд = 0,95 (95 %).
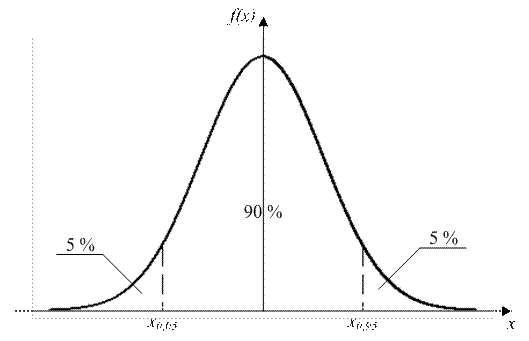
Рис. 2.13. Квантильные оценки случайной величины
Если измерение не представляется возможным повторить, допускается указывать границы результата для доверительной вероятности Pд = 0,99 (99 %).
В особых случаях, например, при измерениях, результаты которых имеют значение для здоровья людей, допускается кроме доверительной вероятности Pд = 0,99, указывать более высокую доверительную вероятность.
2.9. Идентификация законов распределения случайных погрешностей. Критерии согласия
Поскольку порядок обработки результатов измерений зависит от вида законов распределения их погрешностей, на практике часто возникает задача определить, можно ли считать экспериментально полученные данные подчиняющимися тому или иному закону распределения. Для этой цели служат так называемые критерии согласия. Одним из наиболее распространённых среди критериев согласия является критерий c 2 Пирсона.
Допустим, что было получено n значений некоторой случайной величины x. Весь полученный диапазон этих значений разбивают на k интервалов, после чего подсчитывают количество попаданий li значений x в каждый из них. Число интервалов зависит от количества исходных данных, и может быть рассчитано по эмпирической формуле Старджеса
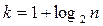, (2.35)
или
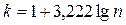, (2.36)
однако следует учитывать, что для корректного применения данного критерия число интервалов должно быть не менее восьми.
По полученным данным рекомендуется построить гистограмму распределения – столбчатую диаграмму, у которой по горизонтальной оси откладываются интервалы, а высота столбцов пропорциональна относительной частоте попаданий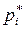 
в каждый из них
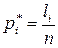. (2.37)
Гистограмма позволяет сделать предварительное суждение о законе распределения, которому подчиняются данные.
Мерой расхождения между экспериментально полученными данными и теоретическим законом распределения, которым они предположительно описываются, является статистика c 2:
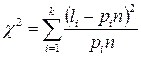, (2.38)
где pi – теоретическая вероятность попадания величины x в i -й интервал для принятого закона распределения.
Для того, чтобы исключить возможные ошибки, ход расчётов удобно свести в таблицу (табл. 2.1).
Полученное значение статистики c 2 сравнивается с теоретическим значением распределения c 2
,
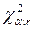где a – уровень значимости критерия,
a = 1 – Pд (2.39)
(рекомендуется принимать a = 0,02 ÷ 0,1);
r – число степеней свободы,
r = k – s – 1; (2.40)
s – число наложенных связей, то есть параметров теоретического закона распределения, определяемых по экспериментальным данным (например, для нормального закона распределения связями будут являться оценки математического ожидания и СКО, используемые для расчёта теоретической вероятности pi).
Таблица 2.1. Расчёты по критерию c2
| Границы интервалов | x1 x2 | x2 x3 | … | xk xk+1 |
| Количество попаданий li | l1 | l2 | … | lk |
Относительная частота попаданий
| 
| 
| … | 
|
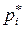
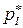
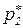
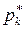
| Теоретическая вероятность попадания pi | p1 | p2 | … | pk |
| pin | p1n | p2n | … | pkn |
| li – pin | l1 – p1n | l2 – p2n | … | lk – pkn |
| (li – pin)2 | (l1 – p1n)2 | (l2 – p2n)2 | … | (lk – pkn)2 |
| 
| 
| … | 
|
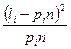
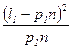
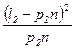
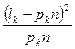
Если выполняется неравенство
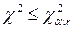, (2.41)
то проверяемая гипотеза (о соответствии экспериментальных данных принятому теоретическому закону распределения) может быть принята. В противном случае, если
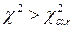, (2.42)
гипотеза должна быть отвергнута.
Следует отметить, что при помощи критериев согласия можно однозначно только отвергнуть рассматриваемую гипотезу, вопрос же о её однозначном принятии только на их основе решён быть не может.
Кроме критерия c 2, в метрологии также достаточно широко применяются критерий w 2 Мизеса-Смирнова, составной критерий, критерий Колмогорова и другие.
Контрольные вопросы
1. Какими способами систематические погрешности могут быть исключены из результата измерений?
2. Какими методами можно скомпенсировать систематические погрешности в процессе измерения?
3. Какой математический аппарат используют для оценки случайных погрешностей?
4. Какие законы распределения случайных погрешностей вам известны?
5. Назовите числовые характеристики законов распределения случайных погрешностей.
6. Что характеризует математическое ожидание случайной погрешности?
7. Что характеризует дисперсия случайной погрешности?
8. При каких условиях возникает случайная погрешность, распределённая по нормальному закону?
9. Назовите параметры нормального закона распределения случайной погрешности.
10. В каком случае возникает случайная погрешность, распределённая по равномерному закону?
11. Как определить математическое ожидание и СКО случайной погрешности, распределённой по равномерному закону?
12. В каком случае возникает случайная погрешность, распределённая по треугольному закону?
13. Как определить математическое ожидание и СКО случайной погрешности, распределённой по треугольному закону?
14. Что такое оценка результата измерения?
15. Какие требования предъявляются к оценкам результатов и погрешностей измерения?
16 Приведите примеры точечных и интервальных оценок результатов и погрешностей измерения?
17. Какую доверительную вероятность рекомендуется принимать при оценке результатов измерения?
18. Для чего используют критерии согласия?
19. Какие критерии согласия используют в метрологии?
20. Можно ли однозначно сделать вывод о принадлежности случайной погрешности тому или иному закону распределения на основе критериев согласия?
3. ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
3.1. Правила записи результатов и погрешностей измерений
Нормативными документами, регламентирующими правила обработки результатов измерений, установлены следующие правила записи их результатов и погрешностей.
1. Погрешность оценки измеряемой величины следует выражать не более чем двумя значащими цифрами. При этом две значащие цифры в погрешности оценки измеряемой величины сохраняют при точных измерениях, либо если первая значащая цифра погрешности не более трёх.
2. Количество знаков после запятой в результате измерения и в его погрешности должно быть одинаковым.
Данные правила распространяются только на окончательную запись результата измерений. В промежуточных расчётах количество цифр должно быть на две больше, чем в окончательном результате.
Пример 1.
Выполнено измерение электрической мощности. Результат измерения
P = 437,6 Вт; абсолютная погрешность DP = 6,56 Вт.
Поскольку первая значащая цифра погрешности измерения больше трёх, то округление результата и погрешности производится до целых: P = (438 ± 7) Вт.
Пример 2.
Записать результат измерения силы электрического тока, если оценка результата измерения I = 79,5 А, а погрешность DI = 1,19 А.
Поскольку первая значащая цифра погрешности измерения не превышает трёх, то округление погрешности производится до двух значащих цифр, то есть результат и его погрешность округляются до одного знака после запятой: I = (79,5 ± 1,2) А.
3.2. Обработка результатов прямых измерений с многократными наблюдениями
При обработке результатов измерений с многократными наблюдениями, согласно ГОСТ 8.736–2011, в качестве оценки результата принимается среднее арифметическое наблюдений
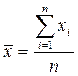, (3.1)
где n – количество наблюдений в серии.
При этом, если наблюдения в серии подчиняются нормальному закону, то их среднее арифметическое подчиняется распределению Стьюдента с n – 1 числом степеней свободы. Мерой рассеяния результата служит СКО среднего арифметического
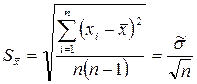, (3.2)
где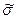 
– оценка СКО наблюдений.
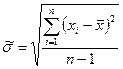. (3.3)
Обработка результатов измерений с многократными наблюдениями выполняется в следующей последовательности:
1. Исключаются известные систематические погрешности.
2. Вычисляется среднее арифметическое исправленных наблюдений
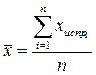. (3.4)
3. Вычисляется оценка СКО наблюдений
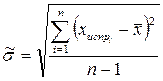. (3.5)
4. Выполняется проверка наблюдений на наличие грубых погрешностей и, при необходимости, их исключение. Для исключения грубых погрешностей используют критерий Граббса. Статистический критерий Граббса исключения грубых погрешностей основан на предположении о том, что группа результатов наблюдений принадлежит нормальному распределению. Для этого вычисляют критерии Граббса G1 и G2, предполагая, что наибольший xиспр.max или наименьший xиспр.min результаты измерений вызваны грубыми погрешностями:
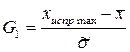; (3.6)
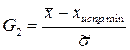. (3.7)
Значения G1 и G2 сравниваются с теоретическим значением Gт критерия Граббса при выбранном уровне значимости q. Критические значения критерия Граббса приведены в табл. 3.1.,
Если G1 > Gт, то xиспр.max исключают, как маловероятное значение. Если G2 > Gт, то xиспр.min исключают, как маловероятное значение. Далее вновь вычисляют среднее арифметическое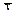 
и оценку СКО наблюдений 
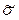, после чего процедуру проверки наличия грубых погрешностей повторяют.
Если G1 < Gт, то xиспр.max не считают промахом и его сохраняют в ряду наблюдений. Если G2 > Gт, то xиспр.min не считают промахом и его сохраняют в ряду наблюдений.
5. Вычисляется оценка СКО результата (среднего арифметического)
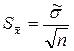. (3.8)
6. Выполняется проверка гипотезы о подчинении результатов наблюдений нормальному закону распределения. При этом, если количество наблюдений n > 50, рекомендуется применять критерии согласия c 2 Пирсона или w 2 Мизеса-Смирнова; если количество наблюдений 15 < n £ 50, предпочтительным является составной критерий; если количество наблюдений n £ 15, их принадлежность к нормальному закону распределения не проверяется.
Проверку гипотезы о том, что результаты измерений подчиняются нормальному распределению, проводят при уровне значимости q от 10 % до 2 %.
