Простейший поток вызовов

 

Определение. Простейшим потоком называется стационарный ординарный поток без последействия. Простейший поток вызовов является наиболее распространенной моделью реального потока вызовов, применяемой в системах массового обслуживания, в том числе в теории телетрафика. Действительно, как отмечалось при рассмотрении принципов классификации потоков вызовов, поток телефонных вызовов от большой группы абонентов характеризуется отсутствием последействия. Его можно считать ординарным, а при ограничении исследуемого промежутка времени 1-3 ч и стационарным. Аналогичные случайные потоки событий характерны для многих отраслей народного хозяйства.

Математическая модель простейшего потока. Определим вероятности поступления точно k (k=0, 1, 2,…) вызовов на отрезке времени (t₀, t₀+t): pk(t₀, t₀+t). Исследования будем проводить на отрезке времени (t₀, t₀+t+τ), который можно представить состоящим из двух примыкающих друг к другу отрезков: (t₀, t₀+t+τ)=(t₀,+t₀+t)+(t, t+τ).

Для того чтобы в течение отрезка (t₀, t₀+t+τ) поступило точно k вызовов, необходимо, чтобы за первый промежуток времени (t₀, t₀+t) поступило k, или k-1,…, или k-i,…, или 0 вызовов и соответственно за второй промежуток 0, или 1,…, или i,…, или k вызовов.

Введем обозначения: p_k(t₀, t₀+t+τ) с вероятность поступления точно k вызовов за отрезок времени (t₀, t₀+t+τ); p_k-i(t₀, t₀+t) - вероятность поступления точно k-i вызовов за первый отрезок времени (t₀, t₀+t); p_i(t, t+τ) - вероятность поступления точно i вызовов за второй отрезок времени (t, t+τ). Согласно определению простейший поток является стационарным.

Из этого следует, что вероятности поступления того или иного числа вызовов за отрезки времени (t₀, t₀+t+τ), (t₀, t₀+t), (t, t+τ) не зависят от моментов начала отсчета времени, а зависят только от длины отрезков времени. Поэтому упростим обозначения как отрезков времени, так и вероятностей: (t₀, t₀+t+τ) будем обозначать (t+τ); (t₀, t₀ + t) с (t); (t, t+τ) с (τ) и соответственно p_k(t₀, t₀+t+τ) - p_k(t+τ); p_k-i(t₀, t₀+t) - p_k-i(t); p_i(t, t+τ) - p_i(τ).

Простейший поток является потоком без последействия. Поэтому независимыми являются события, заключающиеся в поступлении какого-либо числа вызовов за первый и второй промежутки времени, и вероятность поступления точно k вызовов за время (t+τ) для каждой реализации i=0, 1,…, k составляет pk (t+τ) i=pk-i(t) pi(τ), i=0, 1,…, k. Поскольку реализации с i=0, 1,…, k представляют несовместимые события, то согласно формуле полной вероятности имеем

. (13)

 

Выражение (13) представляет собой систему, состоящую из бесконечного числа уравнений. Устремим отрезок времени τ к нулю. Вследствие ординарности простейшего потока π2 (t, t+τ)=o(t), τ→0. Тем более вероятности поступления точно 2, 3,… вызовов с p₂(τ), p₃(τ),… - есть бесконечно малые более высокого порядка по отношению к τ. Следовательно, в системе ур-ний (13) вероятности p_i имеют конечные значения только при i, равном 0 и 1.

На основании этого (13) преобразуются к виду

 

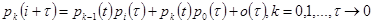. (14)

 

Определяем вероятности p₁(τ) и p₀(τ):

 

.

 

С учетом (10) и (6)

 

 (15)

 

(π₀(τ) - вероятность поступления 0 и более вызовов, т.е. вероятность достоверного события, она равна 1).

Подставим в систему ур-ний (14) полученные значения вероятностей p₁(τ) и p₀(τ).

Затем, перенеся в левую часть уравнений p_k(t), поделим левые и правые части уравнений на τ.

Переходя к пределу, получим

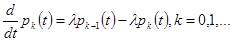. (16)

 

Решив систему дифференциальных ур-ний (16), получим формулу Пуассона

 

. (17)

 

Таким образом, вероятность поступления точно k вызовов простейшего потока за отрезок времени t определяется формулой Пуассона. По этой причине простейший поток также называют стационарным пуассоновским потоком.