2020-04-20
211
Вначале строится D - разбиение в плоскости заданного параметра [2,3,4). Пусть таким параметром является коэффициент усиления k8, который входит в выражение для а4 собственного оператора (3.38). Величины остальных коэффициентов считаются заданными. Решается уравнение D зам (s) = 0 или
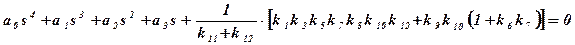
относительно коэффициента k8:
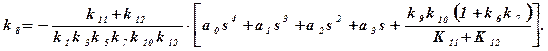
Выражение для k8 приводится к стандартной (для введения в микроЭВМ) форме:
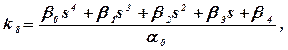(3.39)
где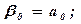 
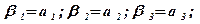
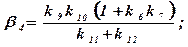
В выражение для коэффициентов уравнения (3.39) подставляются численные значения параметров САР к1 = 1; к2 = 1; к3 = 2; к4 = 1; к5 = 0,5; к6 = 0,7; к7 = 1; к9 = 0,6; к10 = 1; к11 = 1; к12=1; Т1 = 1 с; Т2 = 0,1 с; Т3 = 0,2 с; Т4 = 0,1 с (исходные данные: см. табл. Приложения 2, группа 2, вариант 3). После подстановки численных значений получают: b0 = 0,002; b1 = 0,046; b2 = 0,244; b3=0,71; b4 = 0,48; a0 = - 0,5.
 |
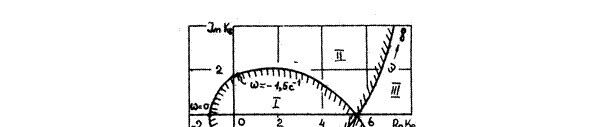Воспользовавшись программой RADIS (см.разд.2), определяют действительную и мнимую составляющие частотной функции k8 для ряда значений частот. Наибольшую частоту колебаний принимают
. Шаг по частоте принимают равным 0,5 с-1. В результате расчета и построения получают кривую D - разбиения для положительных значений частот (рис.3.3). Зеркальным отображением кривой относительно|
|
|
действительной оси дополняют D - разбиения для отрицательных частот колебаний. Крива D - разбиения заштриховывается с левой стороны по мере возрастания частоты колебаний w. Воспользовавшись правилом подсчета корней характеристического уравнения для каждой из выделенных областей D - разбиения определяют область I, соответствующую наибольшему числу корней с отрицательной вещественной частью, т.е. более вероятную область устойчивости САР.
Для проверки устойчивости САР в области I задаются величиной Re k8, взятый из этой области, например Re k8 = 1, и записывают характеристический полином или собственный оператор замкнутой САР в форме (3.38) с числовым значением коэффициентов:
D зам (s) = 0,002s4 + 0,046s3 + 0,244s2 +0,71s + 1,01
Для проверки устойчивости САР по критерию Рауса-Гурвица составляется квадратная матрица Гурвица из коэффициентов а0...ап ;
|
|
|
| ||||||||||||||||
 |  | |  |  | |||||||||||||||
|
|
|
|
 |  |
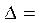
При а0 = 0,002 > 0 анализируются знаки диагональных миноров:
D1 = 0,46 > 0;
D2 = 0,046 × 0,244 - 0,002 × 0,71 = 0,11 > 0;
D3 = 0,046 (0,244 × 0,71 - 0,046 × 1,01) × 0,002 (0,71 × 0,71 -
- 0 × 0,046) = 0,0048 > 0;
D4 = D3 × 1,01 = 0,004848 > 0.
Все диагональные миноры положительные, следовательно САР устойчива и область I D - разбиения (см.рис.3.3) является областью устойчивости САР. Максимальное допустимое значение коэффициента к8 равно 5,58.
|
|
|
Проверка устойчивости САР по одному из критериев является достаточной, однако для овладения навыками оценки устойчивости САР по другим критериям анализируется устойчивость системы по частотным критериям Михайлова и Найквиста.
Оценка устойчивости замкнутой САР по критерию Михайлова производится построением годографа Михайлова по собственному оператору САР (3.38) с соответствующими числовыми значениями коэффициентов а0... а4. Наибольшую частоту wнб и шаг по частоте Dw выбирают равными wнб и Dw, принятыми при построении D - разбиения. В результате расчета и построения на комплексной плоскости получают годограф Михайлова (рис.3.4), который охватывает в положительном направлении четыре квадранта, следовательно, замкнутая САР с характеристическим полиномом четвертого порядка устойчива.
Для проверки устойчивости по критерию Найквиста анализируется АФЧХ разомкнутой системы. Передаточная функция разомкнутой САР (3.34) при принятых значениях коэффициентов имеет вид
 |
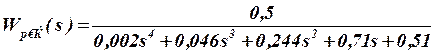(3.40)
Вначале определяется устойчивость разомкнутой системы. Для этого используются собственный оператор (3.37) разомкнутой САР с числовыми значениями коэффициентов:
D раз (s) = 0,002s4 + 0,046s3 + 0,244s2 +0,71s + 0,51.
Используя критерий Рауса-Гурвица, можно показать, что разомкнутая система устойчива. Затем, воспользовавшись программой RADIS, рассчитывается по выражению (3.40) и строится АФЧХ разомкнутой САР. Из представленного на рис.3.5 графика следует, что АФЧХ разомкнутой САР не охватывает точку с координатой (-1; j0), следовательно, замкнутая САР будет устойчива.
 |
