Второго каскада гидроусилителя
При выводе уравнения предполагается: инерционные силы, силы трения и гидродинамические силы, действующие на кромки золотника, пренебрежимо малы по сравнению с силами давления пружины; движение жидкости через жиклер 13 - ламинарное. С учетом принятых допущений уравнение баланса сил, действующих на золотник имеет вид [10]
F з - Fnp =0 (3.18)
где Fз = Sn (рп - рсл) - сила, обусловенная разностью давлений по торцам золотника; Fпр 10 = (Fпр 10)0 - gпр10 (Dz3 - Dz2) - сила противодействия пружины 10; S з - площадь торца золотника; gпр10 - жесткость пружины 10; рз - давление в полости 12. Подставляя выражения для сил Fз и Fпр 10 в равенство (3.18) и выделяя составляющие по отклонениям, можно получить
S з Dрз - gпр10 Dz3 + gпр10 Dz2 = 0
или в безразмерных параметрах
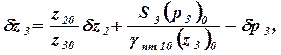 (3.19)
(3.19)
где
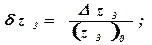
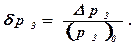
Уравнение баланса расхода жидкости в полости 12, связанной с нижним торцем золотника 11, записывается так:
Qж 13 - Q3 = 0 (3.20)
где 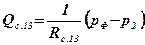 - расход жидкости через жиклер 13;
- расход жидкости через жиклер 13; 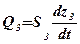 - расход жидкости, обусловленный движением золотника; Rж13 - гидравлическое сопротивление жиклера 13, рф - давление на входе в форсунки (на выходе из дроссельной иглы). Подставляя выражения для Qж 13 , Q3 в уравнение (3.20) и переходя к малым приращениям, можно определить
- расход жидкости, обусловленный движением золотника; Rж13 - гидравлическое сопротивление жиклера 13, рф - давление на входе в форсунки (на выходе из дроссельной иглы). Подставляя выражения для Qж 13 , Q3 в уравнение (3.20) и переходя к малым приращениям, можно определить
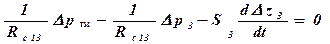
или в безразмерных параметрах
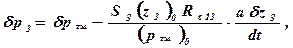 (3.21)
(3.21)
где
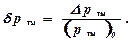
Из совместного решения уравнений (3.19) и (3.21) определится уравнение золотникового распределителя:
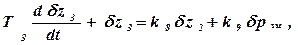 (3.22)
(3.22)
где 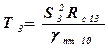 - постоянная времени;
- постоянная времени;
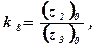
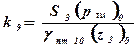 - коэффициенты усиления.
- коэффициенты усиления.
Уравнение сервопоршня 16 второго каскада
Гидроусилителя
При выводе уравнения предполагается, что инерционные сливы, силы трения и гидродинамические силы на дроссельной игле малы по сравнению с силами давления. При принятых допущениях для описания динамики сервопоршня достаточно использовать уравнение баланса расхода жидкости [10,11]
Q 1 - Q2 = 0 (3.23)
где 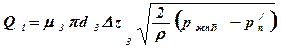 - расход жидкости через окно золотника в правую поршневую полость;
- расход жидкости через окно золотника в правую поршневую полость;
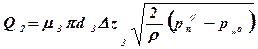 - расход жидкости из левой поршневой полости на слив; mз - коэффициент расхода; dз - диаметр золотника; рп¢, рп² - давления в правой и левой полостях.
- расход жидкости из левой поршневой полости на слив; mз - коэффициент расхода; dз - диаметр золотника; рп¢, рп² - давления в правой и левой полостях.
Так как на поршень, кроме сил давления, не действуют другие силы, то справедливо равенство
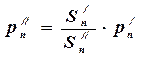 (3.24)
(3.24)
где Sn¢, Sn² - площадь торцев поршня с правой и левой сторон. Тогда из совместного решения уравнений (3.23) и (3.24) с учетом выражений для Q 1 и Q2 можно получить
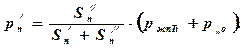
После подстановки полученного выражения для рп¢ в формулу для Q 1 с учетом того, что 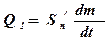 , можно определить
, можно определить
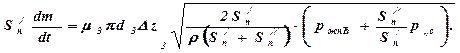
Переходя в последнем выражении к малым приращениям параметров, определяют уравнение сервопоршня 16:
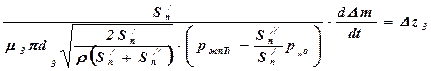
или в безразмерных параметрах
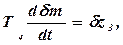 (3.25)
(3.25)
где
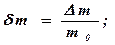
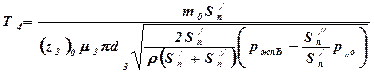
- постоянная времени сервопоршня.
 Уравнение дроссельной иглы
Уравнение дроссельной иглы
Уравнение дроссельной иглы, связывающее массовый расход топлива с перемещением дросельной иглы, определяется зависимостью
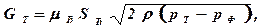
где m д - коэффициент расхода; S д = S д (m) - площадь проходного сечения; р т - давление на входе в дроссельную иглу. Нелинейная расходная характеристика дроссельной иглы линеаризуется разложением в ряд Тейлора:
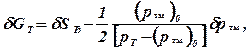 (3.26)
(3.26)
где 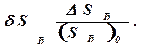
Относительное приращение площади проходного сечения дроссельной иглы dSД связано с относительным его перемещением зависимостью
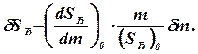 (3.27)
(3.27)
Из совместного решения уравнений (3.26) и (3.27) можно определить линеаризованное уравнение дроссельной иглы:
d G т - k10d m - k11 d pф (3.28)
где 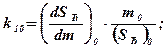
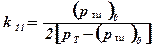
-коэффициент передачи дроссельной иглы.
 2020-04-20
2020-04-20 345
345








